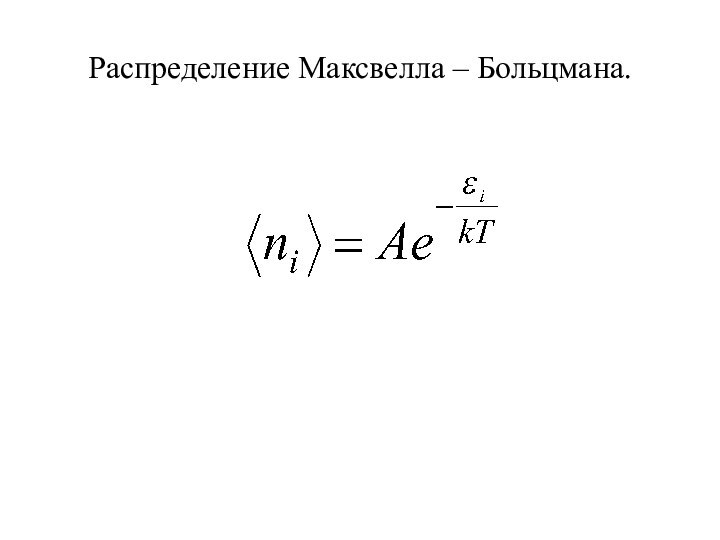Слайд 2
Микроскопические состояния
Различные состояния, отвечающие одной и той же
энергии, имеют различную вероятность. Разумеется, что изолированная система будет
переходть из менее вероятного состояния в более вероятное. Более вероятное состояние реализуется большим количеством микросостояний.
Классическое определение: микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома.
Слайд 3
μ – пространство
Это пространство имеет шесть измерений: px,
py, pz, x, y, z.
Объем элементарной ячейки в этом
пространстве получается путем перемножения уравнений (1):
Слайд 4
μ – пространство
Указание распределения частиц системы по ячейкам
μ – пространства и есть задание его микросостояния. Это
самое точное из возможных описаний термодинамической системы.
Слайд 5
Макроскопические состояния. Статистический вес
Макроскопическое состояние термолинамической системы определяется
макроскопическими параметрами: давлением, температурой и т.п.
Каждому макроскопическому состоянию соответствует
множество микросостояний. Количество таких микросостояний Ω называется статистическим весом данного макросостояния.
Слайд 6
Энтропия
μ – пространство Величина, которая служит для характеристики
вероятности макросостояний, называется энтропией. Эта величина является функцией состояния
термодинамической состемы. По определению
здесь k – постоянная Больцмана (k=1.38×10−23 Дж/K).
Слайд 7
Энтропия – величина аддитивная
Действительно, общий статвес двух подсистем
равен
Поэтому энтропия такой системы имеет вид
Слайд 8
Энтропия (продолжение)
Энтропия для системы из n – подсистем:
Слайд 9
Второе начало термодинамики
Энтропия изолированной системы может только возрастать
либо по достижении максимального значения оставаться постоянной (т.е. не
убывать).
Слайд 10
Сравнение статистических распределений
Слайд 11
Химический потенциал – μ.
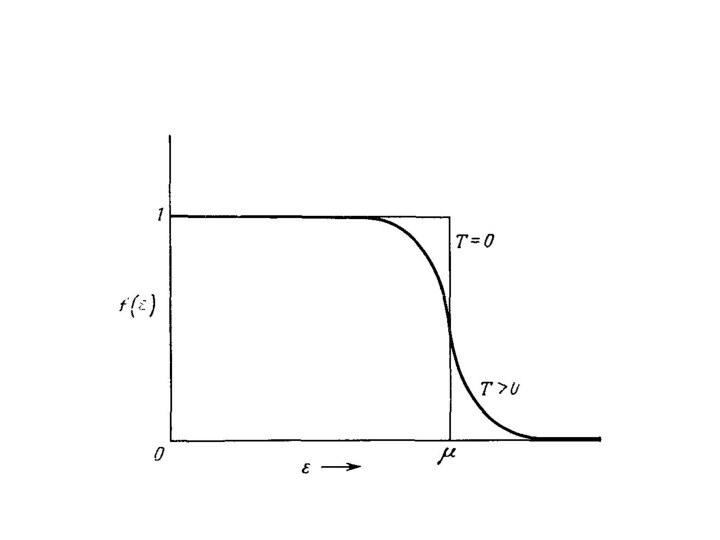
Это распределение Ферми – Дирака
(фермионы)
Слайд 12
Для бозонов – распределение Бозе - Эйнштейна
Слайд 13
Распределение Максвелла – Больцмана.
Слайд 14
Распределение Максвелла
Для классической частицы
Слайд 15
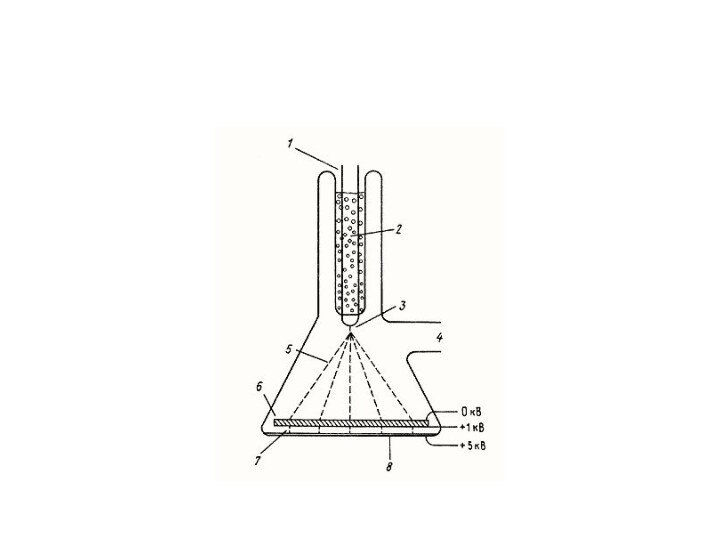
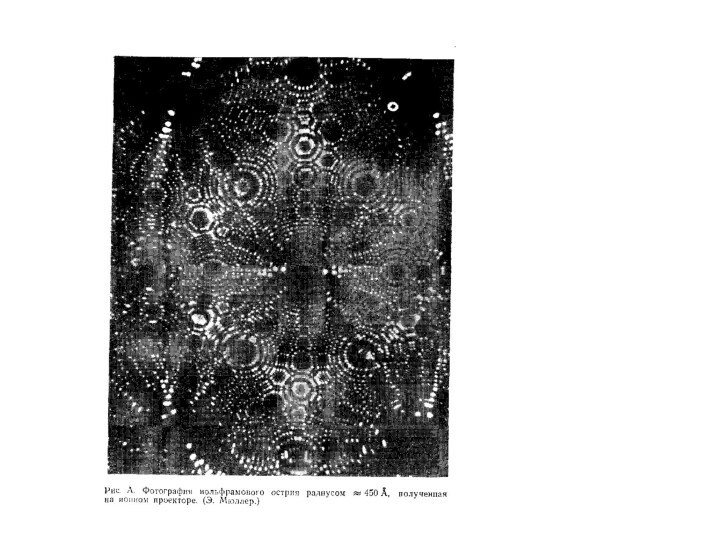
«Ионный микроскоп впервые снабдил человечество средством видеть атомы.
Замечательное достижение, да еще полученное с таким простым прибором»
Р.Фейнман
Слайд 21
Квантовая теория свободных электронов в металле. Электронный газ
Пусть электроны движутся совершенно свободно в пределах образца металла.
Тогда U = 0, а уравнение Шредингера имеет вид:
Решение уравнения (8) очевидно:
Слайд 22
Металл как потенциальная яма. Уровень Ферми
Слайд 23
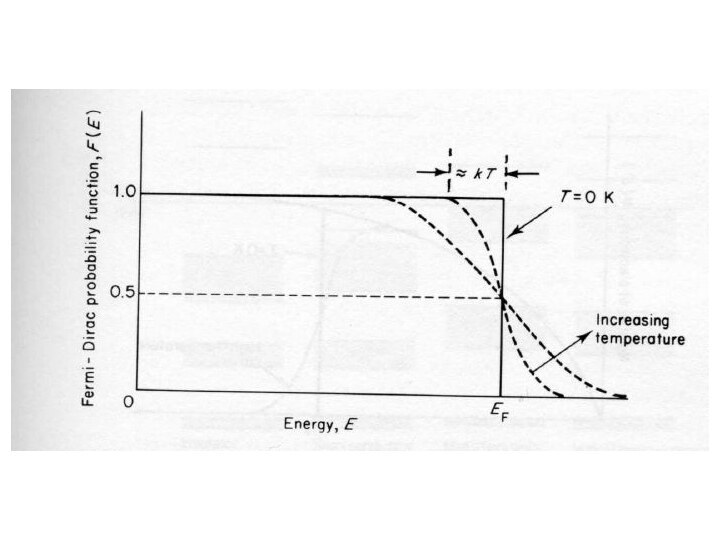
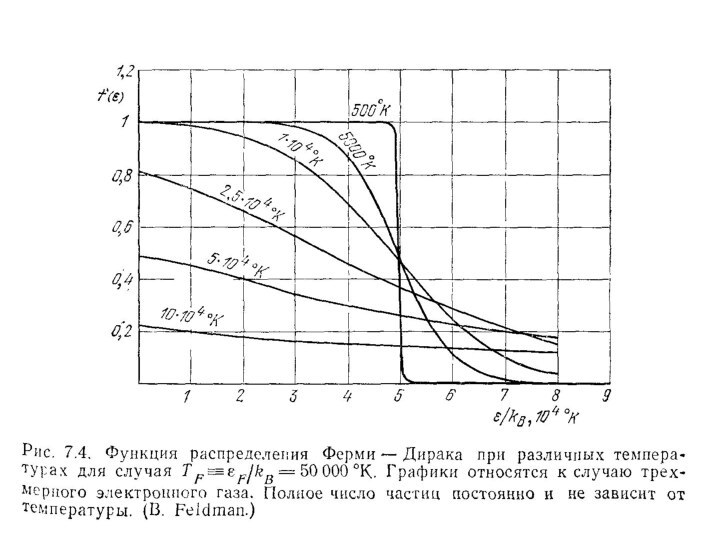
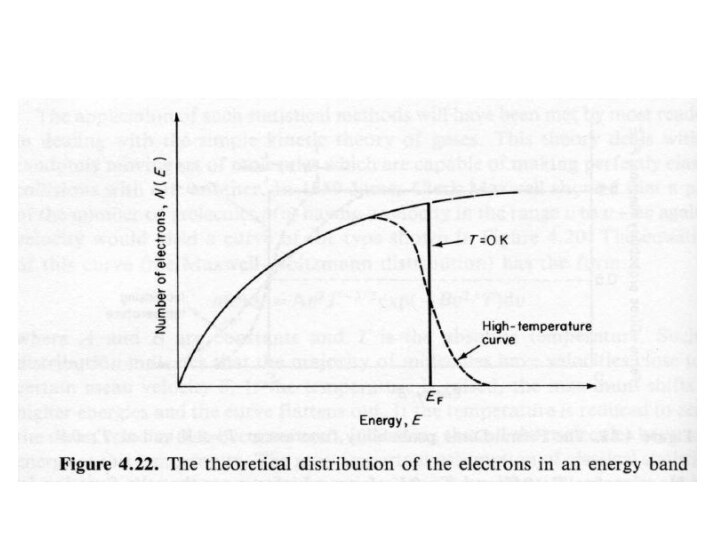
Распределение Ферми-Дирака для свободных электронов
Слайд 26
Энергия Ферми системы невзаимодействующих фермионов — это увеличение
энергии основного состояния системы при добавлении одной частицы. Что
эквивалентно химическому потенциалу системы в ее основном состоянии при абсолютном нуле температур. Энергия Ферми может также интерпретироваться как максимальная энергия фермиона в основном состоянии при абсолютном нуле температур.
Слайд 27
Физический смысл уровня Ферми: вероятность попадания частицы на
уровень Ферми составляет 0,5 при любых температурах.
Название дано в
честь итальянского физика Энрико Ферми.
Слайд 30
Энри́ко Фе́рми (итал. Enrico Fermi, в профессиональной речи
физиков: Ферми́; 29 сентября 1901, Рим — 28 ноября 1954,
Чикаго)
Слайд 31
Температура Ферми
TF ≈ 60000 K для металлов
Слайд 32
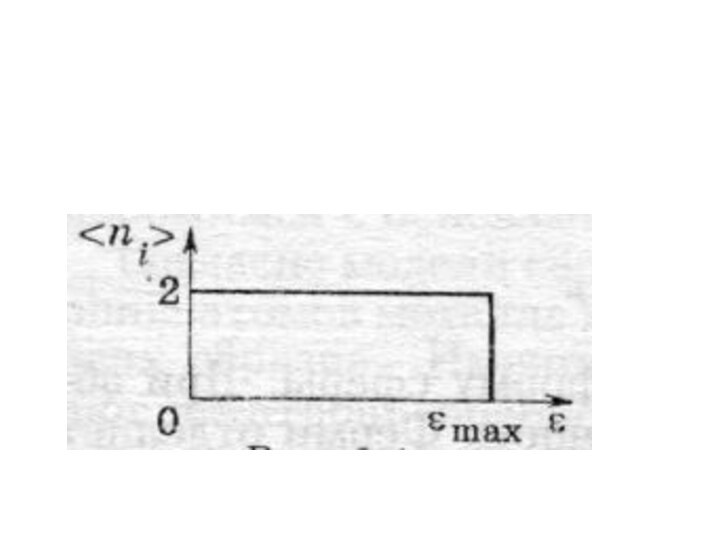
Вырожденный электронный газ
T
εF – вырожденный электронный газ;
T >>TF или kT >>
εF – невырожденный электронный газ.
Слайд 33
Квантовая теория свободных электронов в металле. Электронный газ
Пусть электроны движутся совершенно свободно в пределах образца металла.
Тогда U = 0, а уравнение Шредингера имеет вид:
Решение уравнения (1) очевидно:
Слайд 34
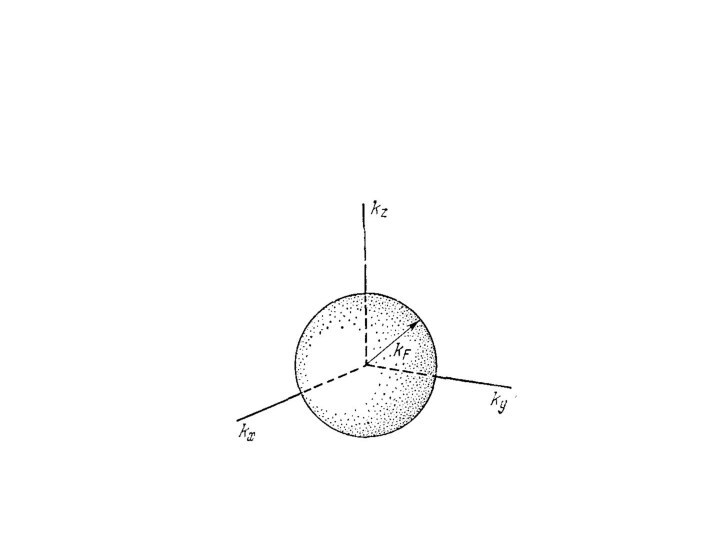
Поверхность Ферми
Изоэнергетическая поверхность в k – пространстве (p=ħk)
В
случае свободных электронов поверхность описывается уравнением:
и имеет форму сферы
Слайд 36
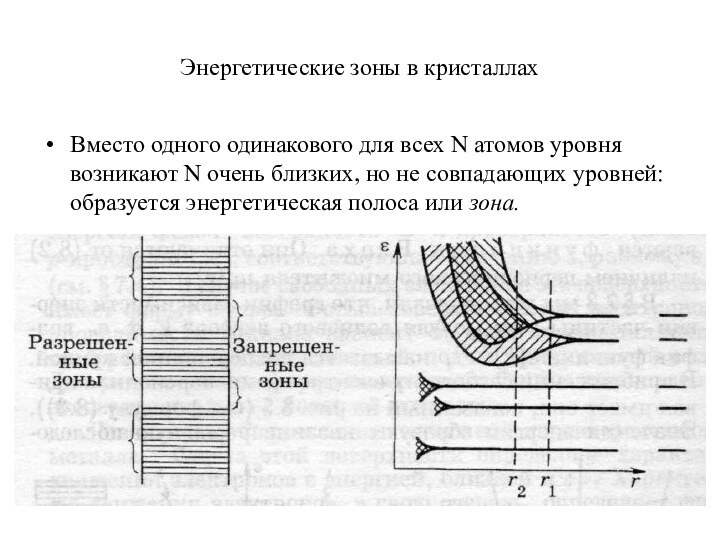
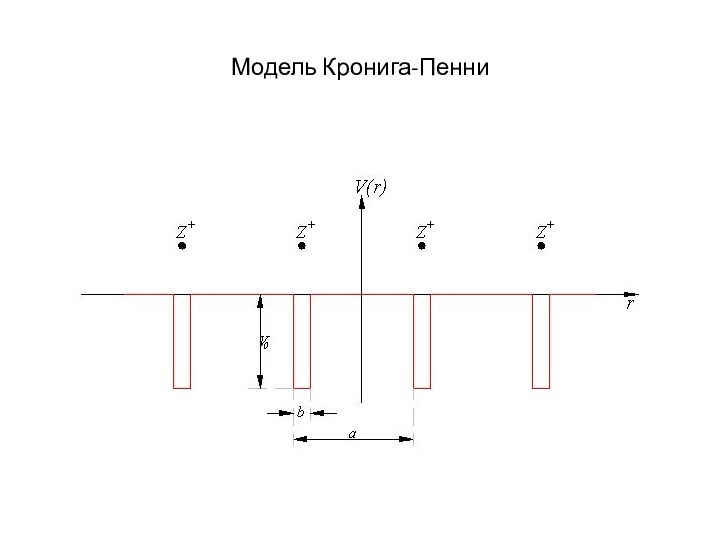
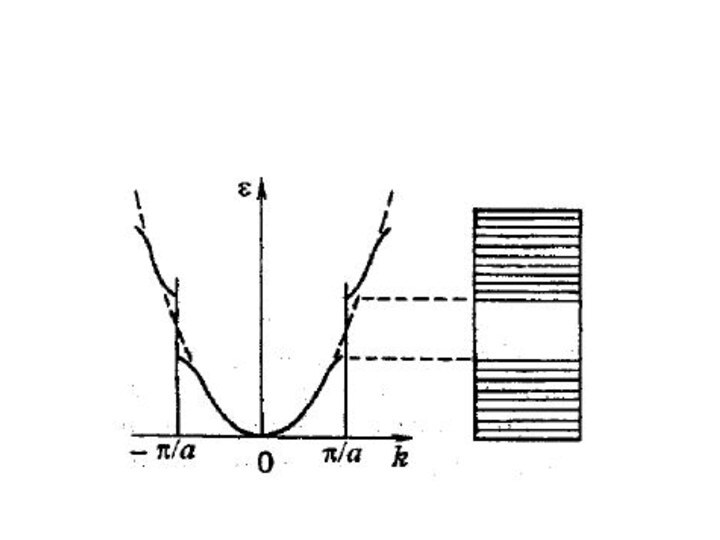
Энергетические зоны в кристаллах
Вместо одного одинакового для всех
N атомов уровня возникают N очень близких, но не
совпадающих уровней: образуется энергетическая полоса или зона.
Слайд 39
Функции Блоха
Уравнение Шредингера имеет вид
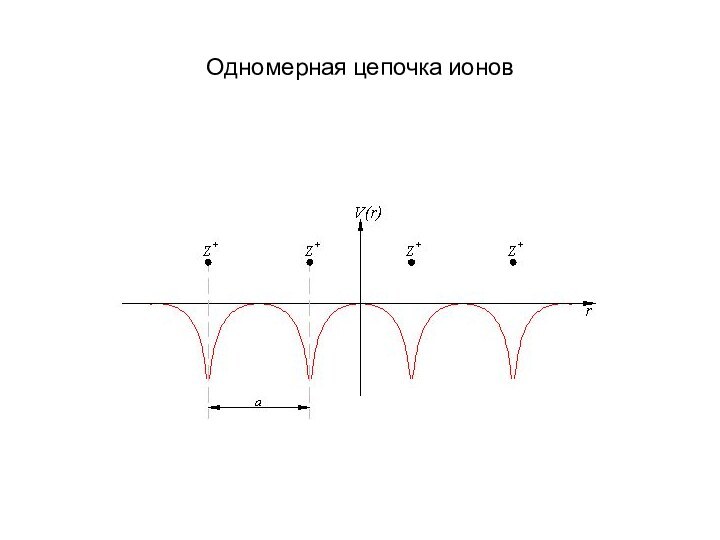
Здесь U – периодический
потенциал:
Слайд 40
Феликс Блох (нем. Felix Bloch; 23 октября 1905, Цюрих —
10 сентября 1983, Цюрих)
Слайд 41
Функции Блоха (продолжение)
Функция uk имеет периодичность потенциала
Слайд 44
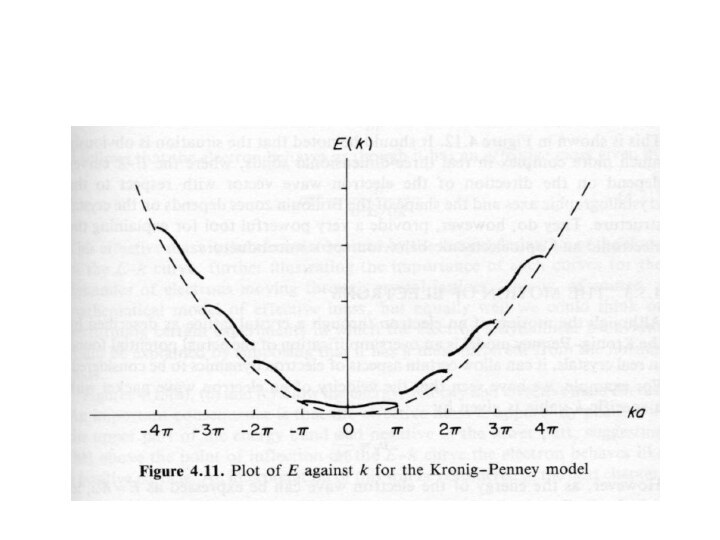
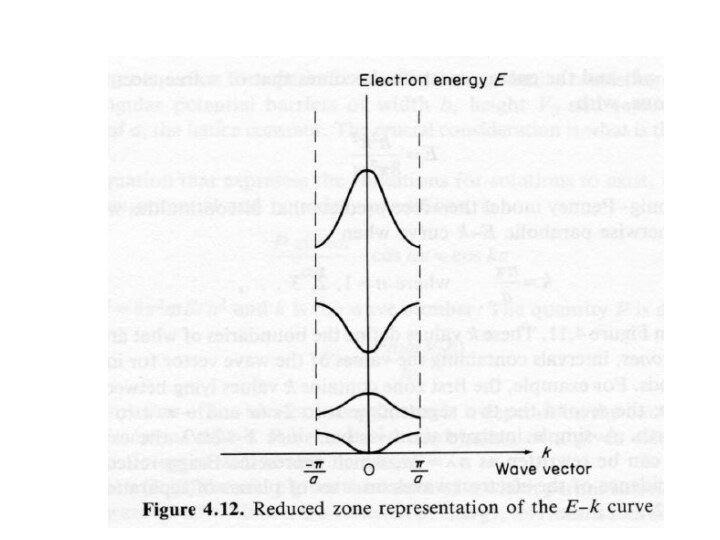
Зона Бриллюэна
Область k-пространства, внутри которой энергия электрона в
кристалле изменяется квазинепрерывно, называется зоной Бриллюэна.
Слайд 49
Квантовая теория электропроводности
Удельное электрическое сопротивление металлов:
Складывается из примесного
и колебательного.
Дрейфовая скорость:
Слайд 50
Взаимодействие с кристаллической решеткой дает силу «трения» Fтр=−rv
Уравнение
движения имеет вид:
m* – эффективная масса электрона. При отсутствии
внешнего электрического поля уравнение (1) имеет вид
Слайд 51
Решение уравнения (2) имеет вид:
vдр (0) – значение
дрейфовой скорости в момент выключения поля. Из (3) следует,
что время релаксации равно
Слайд 52
Теперь силу трения можно записать в виде Fтр=−(m*/τ)vдр
В
устанавившемся режиме (dv/dt=0) уравнение (1) можно записать в виде
Слайд 53
Установившаяся плотность тока j равна произведению vдр, −e
и n:
С другой стороны, из уравнения j=σE следует, что
удельная электропроводность равна
Слайд 54
Сравним с классической формулой
Здесь τ/ - среднее время
свободного пробега, m – масса электрона (Друде, Лоренц)
τ/ ~1/
√T
Слайд 55
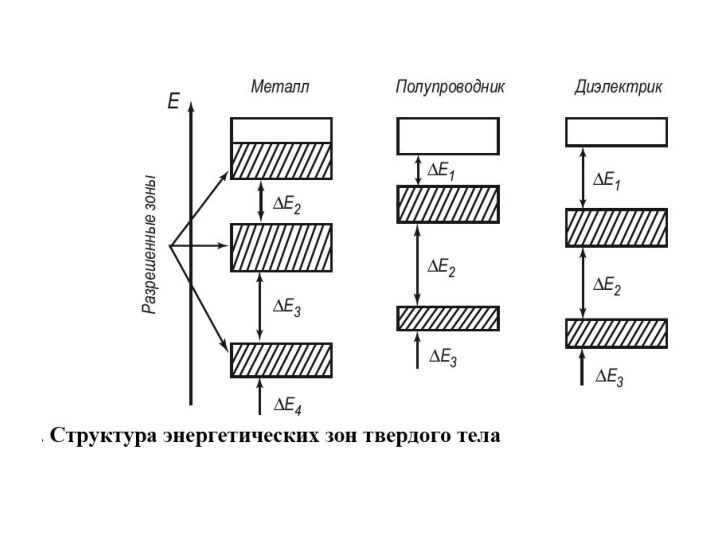
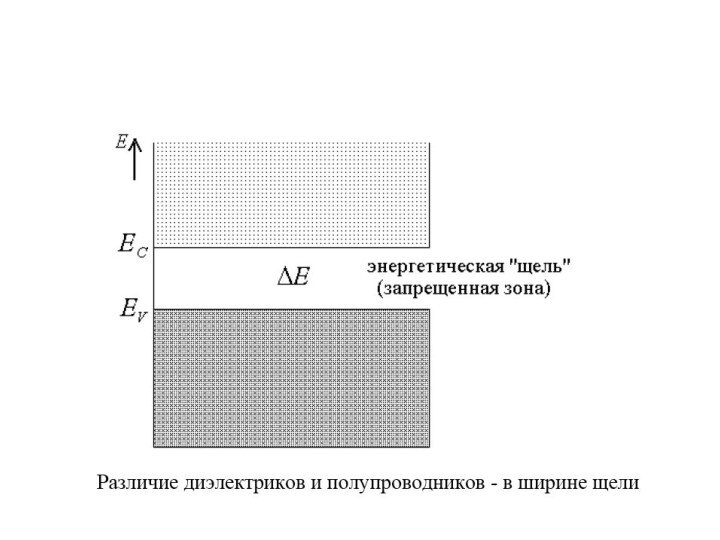
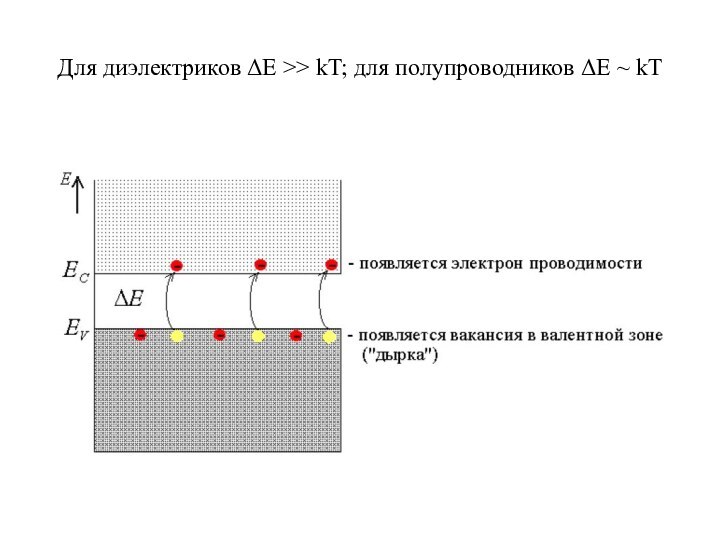
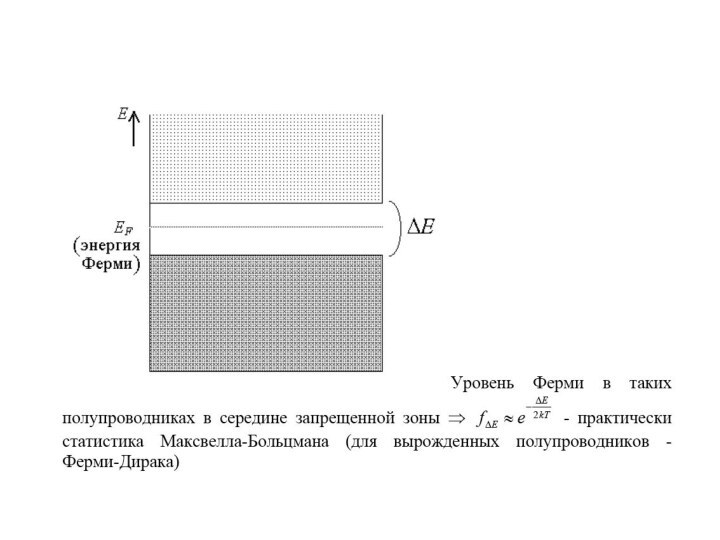
Для диэлектриков ΔE >> kT; для полупроводников ΔE
~ kT
Слайд 57
Для нормальных – не вырожденных и чистых бездефектных
полупроводников – вероятность перескока много меньше единицы, поэтому
Слайд 69
Подвижность носителей тока: v = μ E
Слайд 71
Эффективная масса носителей тока
Анализ движения электрона в периодическом
поле кристалла под действием электрической силы F дает для
ускорения электрона выражение:
Здесь E(k) – полная энергия электрона, k – его волновой вектор.
Слайд 72
Сравнение этих двух формул дает выражение для эффективной
массы носителей тока
Эффективная масса носителей тока:
Слайд 73
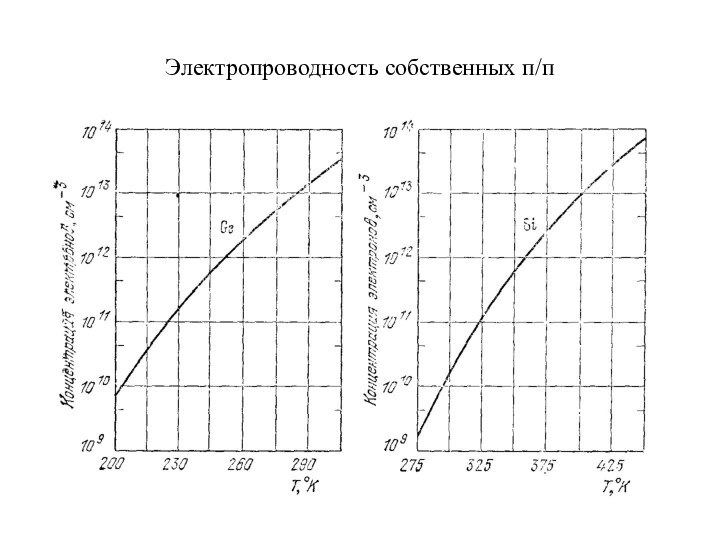
Электропроводность собственных п/п
эффективной массы
Слайд 74
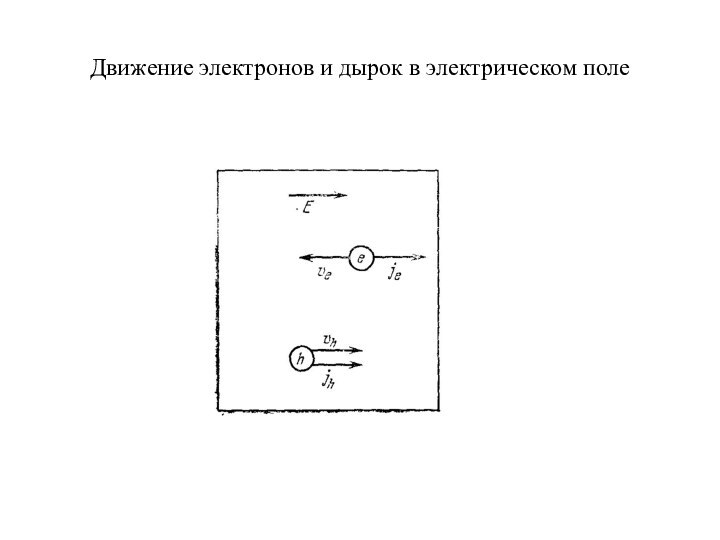
Движение электронов и дырок в электрическом поле
Слайд 75
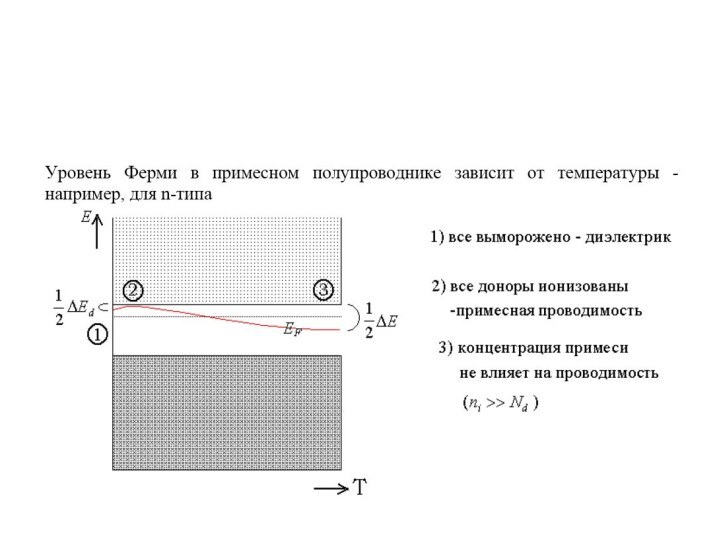
Температурная зависимость электропроводности п/п
Концентрация носителей тока в собственном
п/п:
Слайд 76
Концентрация носителей тока
Где С – слабо зависит
от температуры (по сравнению с exp)
Эффективная плотность состояний в
зоне проводимости
Эффективная плотность состояний в валентной зоне
Слайд 77
Концентрация носителей тока
Концентрация электронов в зоне проводимости
Концентрация
дырок в валентной зоне
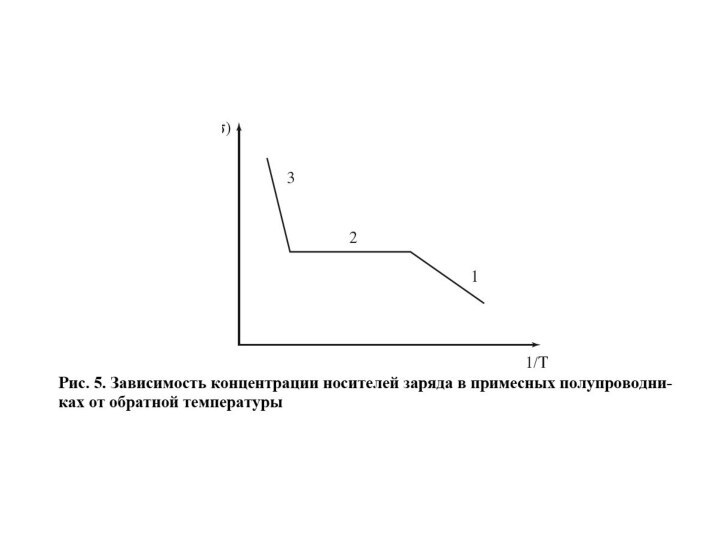
Слайд 78
Зависимость концентрации носителей тока от температуры