Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Теория множеств

Содержание

2. Способы задания множеств:Перечислением: например,
3. L – множество букв, из которых состоит
4. Множество D содержится в множестве М. Обозначается
5. Пустое множество – это множество, не содержащее
6. Конечное множество содержит конечное число элементов,Бесконечное множество
7. AB1. Множества А и В не имеют
8. AB2. Множества А и В имеют общие элементы (заштрихованная часть).
9. AB3. Множество В (строго) содержится в множестве
10. A, B4. Множества А и В равны. Обозначение: А=В
11. Запись АВ означает, что возможно АВ и
12. Операции над множествамиОбъединение (или сумма) множеств А
13. Пересечение множеств А и В – это
14. Разность множеств А и В – это
15. Если В  А, то разность А\ В называется дополнением множества В до множества А.АU
16. Универсальное множество – это множество, относительно которого
17. Итак, возможны соотношения:
18. Всегда ли выполняется соотношение |AB|
19. В общем случае выполняются такие соотношения:|AB| =
20. Из каких элементов состоят множества А и
21. 1. А – множество всех белок, бегающих
22. 3. А – множество книг, В –
23. Некоторые свойства объединения и пересечения множествАА=ААА=АА=АА=
24. АВ=ВА (коммутативность операции объединения)АВ=В А (коммутативность операции
25. Вспомните какие-либо произведения (проза, стихи, кинофильмы и
26. Классификация – представление некоторого множества в виде объединения непустых попарно не пересекающихся подмножеств.
27. Пусть U – множество всех студентов нашего
28. АВUIVIIIIII
29. Группа, состоящая из 20 человек, отправилась в
30. Можно ли, воспользовавшись понятием «множество», точно определить,
31. Как записать следующие соотношения?Объект d не является
32. Скачать презентацию
33. Похожие презентации

Способы задания множеств:Перечислением: например, А = {0,1,2,3,4,5,6,7,8,9} – множество цифрЗаданием общего свойства всех элементов множества. Например, множество всех букв латинского алфавита можно определить так:В = {х |

Теория множествМножество - это совокупность различных элементов, мыслимая как единое целое

L – множество букв, из которых состоит слово «анаконда». Какова численность элементов

Множество D содержится в множестве М. Обозначается D  ММножество Е не

Пустое множество – это множество, не содержащее ни одного элемента, обычно обозначается

Конечное множество содержит конечное число элементов,Бесконечное множество содержит бесконечное число элементов.Чёткое множество

AB1. Множества А и В не имеют общих элементов (не пересекаются).Соотношения между

AB2. Множества А и В имеют общие элементы (заштрихованная часть).

AB3. Множество В (строго) содержится в множестве А (или «множество В (строго)

A, B4. Множества А и В равны. Обозначение: А=В

Запись АВ означает, что возможно АВ и возможно А=ВВ этом случае говорят,

Операции над множествамиОбъединение (или сумма) множеств А и В – это множество

Пересечение множеств А и В – это множество С=АВ, такое, что:1) если

$Разность множеств А и В – это множество С=А\ В, такое, что:если$ $Если В  А, то разность А\ В называется дополнением множества В до множества А.АU$ Универсальное множество – это множество, относительно которого все рассматриваемые множества являются подмножествами.

Универсальное множество – это множество, относительно которого все рассматриваемые множества являются подмножествами.

Всегда ли выполняется соотношение |AB| = |A| + |B| ?Всегда

$В общем случае выполняются такие соотношения:|AB| = |A| + |B| - |АВ||A\B|$ Из каких элементов состоят множества А и В?А={x I x – животное}{x

1. А – множество всех белок, бегающих по городку в данный момент

3. А – множество книг, В – множество словарных изданий, С –

Некоторые свойства объединения и пересечения множествАА=ААА=АА=АА=

АВ=ВА (коммутативность операции объединения)АВ=В А (коммутативность операции пересечения)(АВ)С = А(ВС) (ассоциативность операции

Вспомните какие-либо произведения (проза, стихи, кинофильмы и т.д.), название которых именует некоторое

Классификация – представление некоторого множества в виде объединения непустых попарно не пересекающихся подмножеств.

Пусть U – множество всех студентов нашего университета, α – свойство «быть

Группа, состоящая из 20 человек, отправилась в туристическую поездку. Из них 14

Можно ли, воспользовавшись понятием «множество», точно определить, что такое «анаграмма»? Примеры анаграмм: вертикаль — кильватер

Как записать следующие соотношения?Объект d не является элементом множества, являющегося пересечением множеств

Какие из следующих соотношений верны?с{а,в,с}d{а,в,с}{а,в,с}{а,в,с}{а,в,с}{а,в,с}{а,в}{а,в,с}с{в,{с}}{с}{в,{с}}

Слайды презентации

Слайд 2 Способы задания множеств:
Перечислением: например,

А = {0,1,2,3,4,5,6,7,8,9} –

множество цифр
Заданием общего свойства всех элементов множества. Например, множество всех букв латинского алфавита можно определить так:
В = {х | х – буква латинского алфавита}

Слайд 3 L – множество букв, из которых состоит слово

L – множество букв, из которых состоит слово «анаконда». Какова численность

«анаконда». Какова численность элементов множества L?
H – множество букв,

из которых состоит слово «канон». Сравните численности множеств L и H.

Численность множества М (или мощность множества М) – количество элементов, составляющих множество М, обозначается I М I

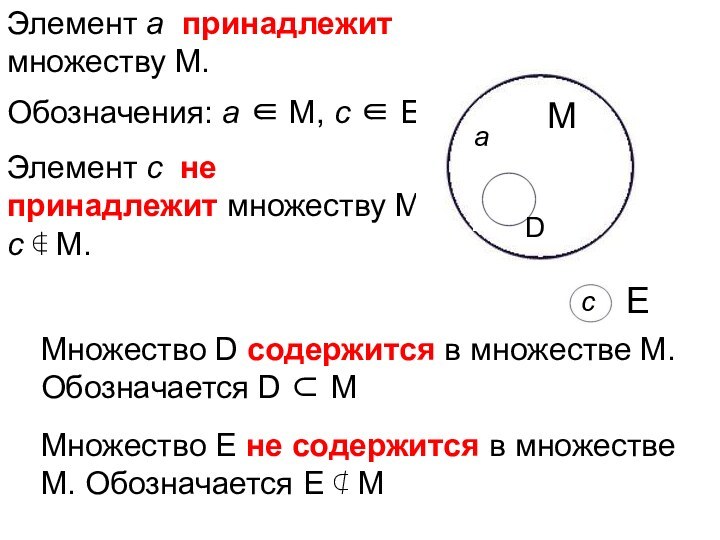
Слайд 4 Множество D содержится в множестве М. Обозначается D

 М
Множество Е не содержится в множестве М. Обозначается

Е  М

Элемент а принадлежит множеству М.
Обозначения: а  М, с  Е.
Элемент с не принадлежит множеству М, с  М.

Слайд 5
Пустое множество – это множество, не содержащее ни

Пустое множество – это множество, не содержащее ни одного элемента, обычно

одного элемента, обычно обозначается символом . I  I

= 0

Единичное множество – это множество, содержащее только один элемент. I М I = 1

Слайд 6 Конечное множество содержит конечное число элементов,

Бесконечное множество содержит

Конечное множество содержит конечное число элементов,Бесконечное множество содержит бесконечное число элементов.Чёткое

бесконечное число элементов.
Чёткое множество включает только такие элементы, принадлежность

которых к данному множеству не вызывает сомнений.

Нечёткое множество включает элементы, которые могут быть отнесены к этому множеству только с определённой степенью вероятности.

Слайд 7 A
B
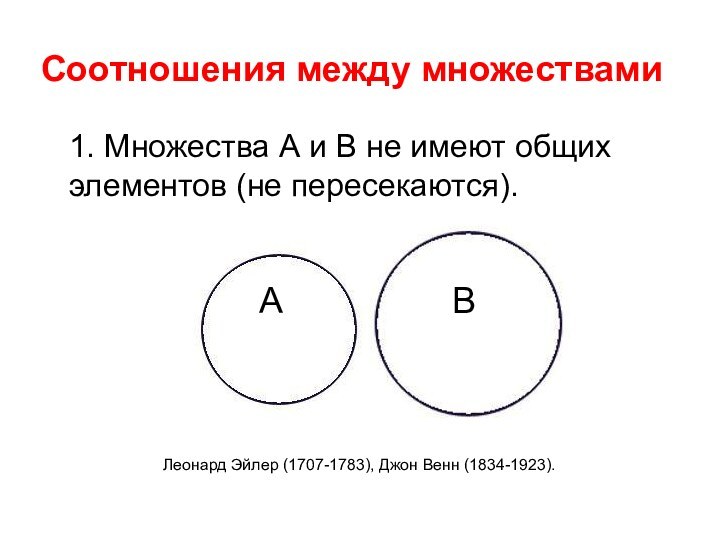
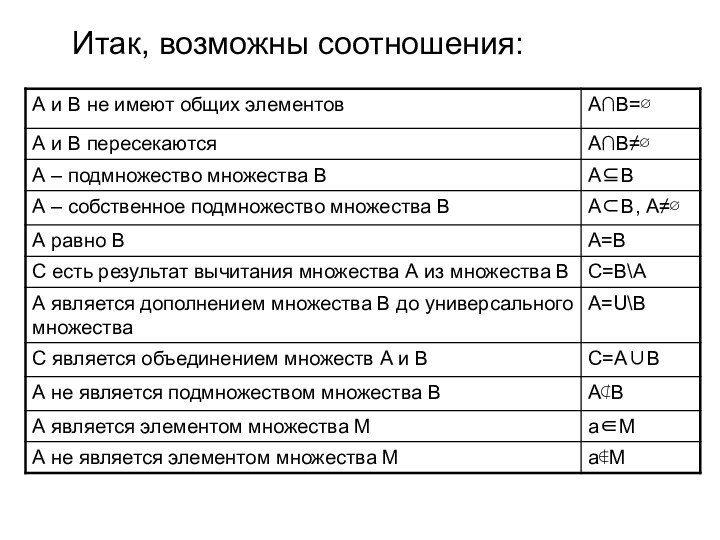
1. Множества А и В не имеют общих

AB1. Множества А и В не имеют общих элементов (не пересекаются).Соотношения

элементов (не пересекаются).
Соотношения между множествами
Леонард Эйлер (1707-1783), Джон Венн

(1834-1923).

Слайд 8 A
B
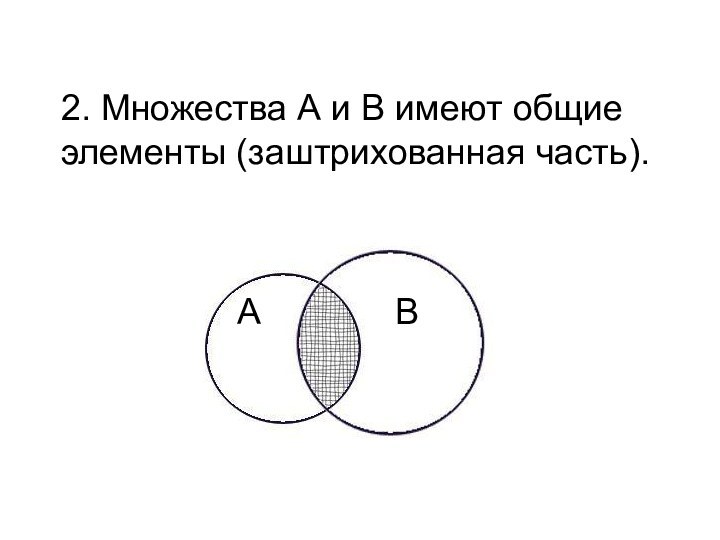
2. Множества А и В имеют общие элементы

(заштрихованная часть).

Слайд 9 A
B
3. Множество В (строго) содержится в множестве А

AB3. Множество В (строго) содержится в множестве А (или «множество В

(или «множество В (строго) включено в множество А», или

«множество В является (строгим) подмножеством множества А).
Обозначение: В  А

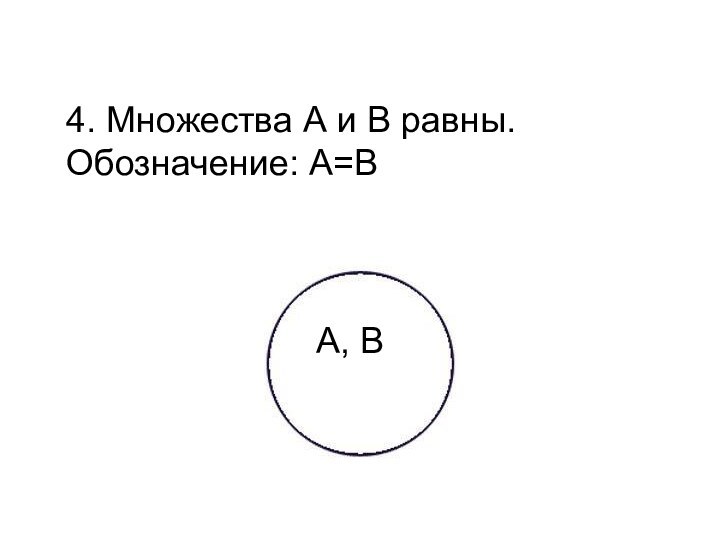
Слайд 10 A, B
4. Множества А и В равны. Обозначение:

А=В

Слайд 11 Запись АВ означает, что возможно АВ и возможно

А=В
В этом случае говорят, что множество А нестрого включено

в множество В
(или «А - нестрогое подмножество множества В», «А нестрого содержится в В»)

Множество В называют собственным подмножеством множества А, если В  А, причём В не является пустым множеством и В не совпадает с А.

Слайд 12 Операции над множествами
Объединение (или сумма) множеств А и

Операции над множествамиОбъединение (или сумма) множеств А и В – это

В – это множество С=АВ, такое, что:
каждый элемент множества

А содержится в С,
каждый элемент множества В содержится в С,
никаких других элементов в С нет.

Слайд 13 Пересечение множеств А и В – это множество

Пересечение множеств А и В – это множество С=АВ, такое, что:1)

С=АВ, такое, что:

1) если элемент х содержится как в

А, так и в В, то х содержится в С,

2) никаких других элементов в С нет.

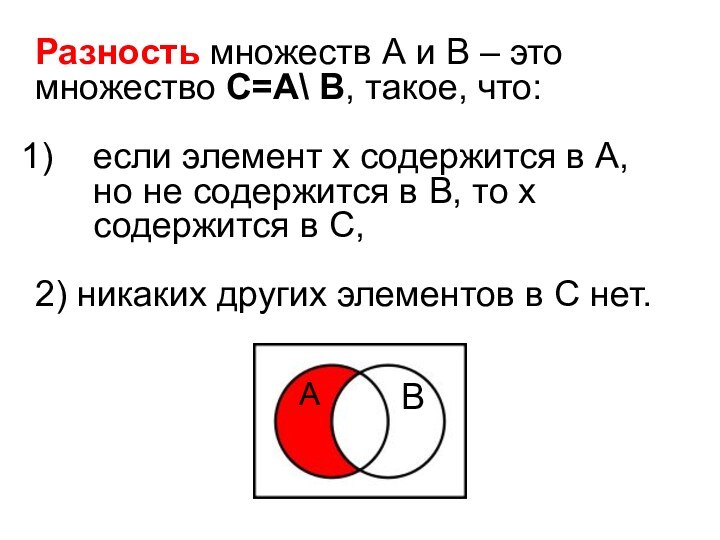
Слайд 14 Разность множеств А и В – это множество

$Разность множеств А и В – это множество С=А\ В, такое,$

С=А\ В, такое, что:

если элемент х содержится в А,

но не содержится в В, то х содержится в С,

2) никаких других элементов в С нет.

Слайд 15 Если В  А, то разность А\ В

$Если В  А, то разность А\ В называется дополнением множества В до множества А.АU$

называется дополнением множества В до множества А.

А
U

Слайд 16 Универсальное множество – это множество, относительно которого все

Универсальное множество – это множество, относительно которого все рассматриваемые множества являются

рассматриваемые множества являются подмножествами. Обозначается U.

Дополнение множества А до

универсального множества обозначается А

Слайд 17 Итак, возможны соотношения:

Слайд 18 Всегда ли выполняется соотношение |AB| = |A| +

|B| ?
Всегда ли выполняется соотношение?

|A\B| = |A| - |B|

Мощность множества – количество его элементов. |А| - мощность множества А

Слайд 19 В общем случае выполняются такие соотношения:

|AB| = |A|

В общем случае выполняются такие соотношения:|AB| = |A| + |B| -

+ |B| - |АВ|

|A\B| = |A| - |B| +

|В\А|

Слайд 20 Из каких элементов состоят множества А и В?
А={x

I x – животное}{x I x - хищник}

А={x I

x – животное}{x I x - хищник}

Слайд 21 1. А – множество всех белок, бегающих по

1. А – множество всех белок, бегающих по городку в данный

городку в данный момент времени; В – множество млекопитающих,

населяющих Землю в данный момент времени
Каковы элементы множеств АВ, АВ и А\В?
2. А – множество людей, присутствующих сейчас в данной аудитории, В – множество студентов Оксфордского университета.
Каковы элементы множества А\В?

Слайд 22 3. А – множество книг, В – множество

словарных изданий, С – множество электронных книг.
Каковы элементы множества

D, если оно определено так: D=(АВ)\С?

Слайд 23 Некоторые свойства объединения и пересечения множеств
АА=А
АА=А
А=А
А=

Слайд 24 АВ=ВА (коммутативность операции объединения)

АВ=В А (коммутативность операции пересечения)

(АВ)С

= А(ВС) (ассоциативность операции объединения)

(АВ)С = А(ВС) (ассоциативность операции

пересечения)

Слайд 25 Вспомните какие-либо произведения (проза, стихи, кинофильмы и т.д.),

Вспомните какие-либо произведения (проза, стихи, кинофильмы и т.д.), название которых именует

название которых именует некоторое множество или операцию над множествами.

Какие из этих множеств упорядоченные, какие неупорядоченные
Например, «Трое в лодке, не считая собаки»: А – люди, В – собаки, С – находящиеся в лодке, IАI=3, IВI=1. Можно ли эту ситуацию описать так: (АВ)С – люди и собаки в лодке?
Множества А, В, С неупорядоченные.

Слайд 26 Классификация – представление некоторого множества в виде объединения

непустых попарно не пересекающихся подмножеств.

Слайд 27 Пусть U – множество всех студентов нашего университета,

Пусть U – множество всех студентов нашего университета, α – свойство

α – свойство «быть студентом 2-го курса», β –

свойство «быть спортсменом»,
А – множество всех студентов 2-го курса,
В – множество всех спортсменов

Каковы элементы множеств А и В ?

Какую классификацию множества U задают свойства α, β ?

Слайд 28 А
В
U
IV
II
I
III

Слайд 29 Группа, состоящая из 20 человек, отправилась в туристическую

Группа, состоящая из 20 человек, отправилась в туристическую поездку. Из них

поездку. Из них 14 человек знают английский язык, 5

– итальянский, только один человек знает оба языка.
Сколько человек не знает ни английского, ни итальянского? Какие операции над множествами вы использовали для ответа на вопрос?

Слайд 30 Можно ли, воспользовавшись понятием «множество», точно определить, что

Можно ли, воспользовавшись понятием «множество», точно определить, что такое «анаграмма»? Примеры анаграмм: вертикаль —

такое «анаграмма»?
Примеры анаграмм:
вертикаль — кильватер
апельсин — спаниель
старорежимность — нерасторжимость
австралопитек —

ватерполистка
покраснение — пенсионерка
равновесие — своенравие
стационар — соратница
обезьянство - светобоязнь
антиквар - травинка
истопник - синоптик