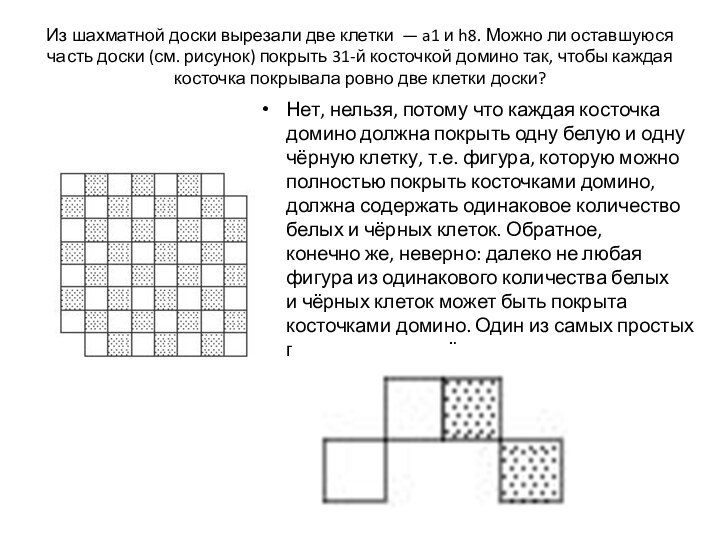
60 км/ч, остальную часть пути – со скоростью 80
км/ч. Какова средняя скорость движения автомобиля?Пусть – S (км) – весь
путь, который прошел
автомобиль.
¾* S(км) – путь, который проехал автомобиль со скоростью 60 км/ч.
¼ *S(км) – оставшаяся часть пути, которую автомобиль прошел со скоростью 80 км/ч
Средняя скорость автомобиля:V=S/T,
для нахождения скорости нам нужно найти время на 1 участке пути (¾ S(км) )
и на втором участке пути ( ¼ S(км))
T=S/V
1 участок – T= (3/4*S) /60=3s/(4*60)=s/20(ч)
2 участок - T= (1/4*S) /80=s/(4*80)=s/320(ч)
Общее время, затраченное автомобилем
на 2-х участках пути равна 17s/320 (ч).
Средняя скорость автомобиля:V=S/T,
V=S/ (17*S/320)= 320/17 (КМ/Ч)
Ответ: