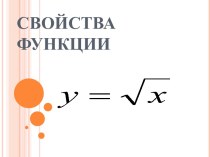Презентация на тему по математике на тему Арифметический корень (1 курс СПО)

умения по теме «Арифметический корень»
Задачи:
ввести понятие арифметического корня с

натуральным показателем;
рассмотреть свойства;
сформировать умения вычислять арифметические корни натуральной степени;
сформировать умения вычислять корни нечетной степени из отрицательного числа;

(x2 – 4) (x2 + 4) = 0.
Это уравнение равносильно совокупности уравнений: x2 – 4 = 0, x2 + 4 = 0.
Т.к. x2 + 4 = 0 не имеет

решения на множестве действительных чисел, то остается второе уравнение, решаем его: x2 – 4 = 0, x2 = 4, отсюда х1 = 2, х2 = -2.
Наше уравнение имеет два действительных корня, которые называются корнями четвертой степени из числа 16, а положительный корень (число 2)   арифметическим корнем  четвертой степени из числа 16 и обозначается .

называется неотрицательное число, n - ая  степень которого равна a.

Т. е.
a называется подкоренным выражением

Корень третьей степени называют кубическим корнем.
Например:
  Действие, при котором

находится корень n-ой степени, называется извлечением корня n-ой степени.
Оно является обратным действию возведения в n-ую степень.

(x-2)2 + 12 ≠ 0, то решаем уравнение x + 4 = 0, откуда x = -4.
Т.к. - 4 

являясь корнем числа - 64, не является арифметическим корнем. Число -4 является корнем числа -64 и обозначается .

30, 33