Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Урок, Презентация Квадратные уравнения

Содержание

2. Решениеквадратных уравнений.
3. А 3x2 – 2x – 5 = 0,Д x2
4. Диофа́нт Александри́йский — древнегреческий математик, живший
5. Повторение пройденного материала.Каков общий вид имеет квадратное
7. Ситуации, в которых может использоваться теорема Виета.
8. Решите следующие задания:Верно ли, что числа 15
9. Приёмы устного решения квадратных уравнений.a x²+ b
10. Решите уравнения, используя свойства коэффициентов:2x² + 3x
12. Самостоятельная работа
14. Домашнее задание.Вариант 1. 2х² – 16x =
15. Скачать презентацию
16. Похожие презентации

Решениеквадратных уравнений.

Главная
Алгебра
Урок, Презентация Квадратные уравнения

А 3x2 – 2x – 5 = 0,Д x2 = 5,И 7x2 +14x = 0,Н x2

Диофа́нт Александри́йский — древнегреческий математик, живший предположительно в III веке н.

Повторение пройденного материала.Каков общий вид имеет квадратное уравнение? а) ах²

Ситуации, в которых может использоваться теорема Виета. Проверка правильности найденных корней. Определение

Решите следующие задания:Верно ли, что числа 15 и 7 являются корнями уравнения

Приёмы устного решения квадратных уравнений.a x²+ b x + c = 0.Основа:

Решите уравнения, используя свойства коэффициентов:2x² + 3x + 1 = 0;5x² –

Домашнее задание.Вариант 1. 2х² – 16x = 0; 5x² – 50x =

Слайды презентации

Слайд 2 Решение
квадратных уравнений.

Слайд 3 А 3x2 – 2x – 5 = 0,
Д x2 =

А 3x2 – 2x – 5 = 0,Д x2 = 5,И 7x2 +14x =

5,
И 7x2 +14x = 0,
Н x2 + 5x + 4 =0
О x2

+ 4x + 4 =0,
Т x2 – 4 = 0,
Ф 2x2 – 11x +5 = 0.

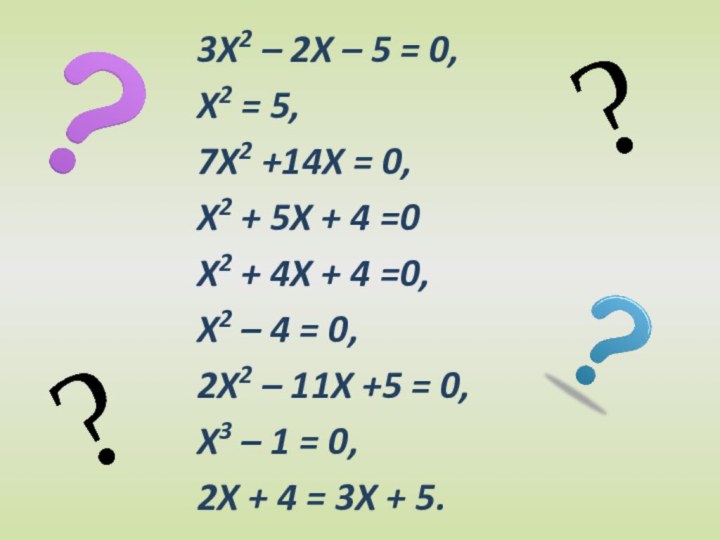
Поле чудес

Слайд 4 Диофа́нт Александри́йский — древнегреческий математик, живший предположительно

Диофа́нт Александри́йский — древнегреческий математик, живший предположительно в III веке

в III веке н. э. Нередко упоминается как «отец

алгебры». Автор «Арифметики» — книги, посвящённой нахождению положительных рациональных решений неопределённых уравнений. В наше время под «диофантовыми уравнениями» обычно понимают уравнения с целыми коэффициентами, решения которых требуется найти среди целых чисел.

Диофант

Слайд 5 Повторение пройденного материала.
Каков общий вид имеет квадратное уравнение?

а) ах² + с = 0;

б) ах²+bх+с=0; в) х²+bх+с=0.
● Какое уравнение называется неполным?, а какое приведённым?
● Сколько корней может иметь кв. уравнение?
● От чего зависит количество корней кв. уравнения?
● Что такое дискриминант кв. уравнения?
● Чему равен дискриминант кв. уравнения?
● Формулы корней кв. уравнения?
● А как выглядит формула корней кв. уравнения в случае D=0?
● Целесообразно ли при решении неполного кв. уравнения применять формулы корней кв. уравнения?
1) D=b²-4ac ; 2) X 1.2= - b ±√D/2a ; 3) X 1,2= - b/2a .

Слайд 6

Слайд 7 Ситуации, в которых может
использоваться теорема Виета.
Проверка

Ситуации, в которых может использоваться теорема Виета. Проверка правильности найденных корней.

правильности найденных корней.
Определение знаков корней квадратного уравнения.
Устное

нахождение целых корней приведённого квадратного уравнения.
Составление квадратных уравнений с заданными корнями.
Разложение квадратного трёхчлена на множители.

Слайд 8 Решите следующие задания:

Верно ли, что числа 15 и

Решите следующие задания:Верно ли, что числа 15 и 7 являются корнями

7 являются корнями уравнения

x² – 22x + 105 = 0 ?
Определите знаки корней уравнения x² + 5x – 36 = 0.
Найдите устно корни уравнения x² – 9x + 20 = 0.
Составьте квадратное уравнение, корнями которого являются числа 3 и 2.
5. Разложите квадратный трёхчлен x² + 2x – 48 на множители.

Слайд 9 Приёмы устного решения квадратных уравнений.
a x²+ b x

Приёмы устного решения квадратных уравнений.a x²+ b x + c =

+ c = 0.
Основа:

f (x) = a x² + b x + c ;
f (1) = a + b + c; f (- 1) = a - b + c.

1.Если a + b + c = 0, то один корень уравнения x = 1, а второй x = c/a.

2.Если a - b + c = 0, то один корень уравнения x = - 1, а второй x = - c/a.

Слайд 10 Решите уравнения, используя свойства коэффициентов:
2x² + 3x +

1 = 0;
5x² – 4x – 9 = 0;
7x²

+ 2x – 5 = 0;
x² + 17x – 18 = 0;
100x² – 97x – 197 = 0.

Слайд 11

Слайд 12 Самостоятельная работа

Слайд 13

Слайд 14 Домашнее задание.
Вариант 1.
2х² – 16x = 0;

5x² – 50x = 0;
x² – 4x –

32 = 0;
x² + 12x + 32 = 0;
x² + 11x – 26 = 0;
5x² – 40x = 0;
x² – 11x + 24 = 0;
4x² – 12x – 40 = 0;
2x² + 13x – 24 = 0.

Вариант 2.
2x² + 16x = 0;
x² – 12x + 27 = 0;
2x² – 6x – 56 = 0;
x² + 9x + 20 = 0;
x² + 8x = 0;
x² – 14x + 40 = 0;
3x² – 18x + 15 = 0;
4x² – 24x + 32 = 0;
x² – 3x + 2,25 = 0.

Повторить §§ 24 – 29.
Решить уравнения по вариантам