- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Complexity and Fragility?
Содержание
- 2. The popular media has given us
- 3. Is there any hope?
- 4. Is there any hope?What is the ultimate showstopper?
- 5. Is there any hope?What is the ultimate showstopper?
- 6. Is there any hope?What is the ultimate
- 7. Robust to uncertainty in environment and componentsEfficient
- 8. Robust EfficientScalableVerifiable with short proofsEngineering design objectives
- 9. Want robustness & efficiency that is verifiably
- 10. Threshold theoremsIID bit sourceErasureErasureError correcting codesE(latency)log(E(error))CodeDecodeThanks to Arum and Ben
- 11. With feedbackIID bit sourceErasureE(latency)log(E(error))CodeDecodeZero error with bounded E(latency) Erasure
- 12. With feedbackIID bit sourceErasureCodeDecodeZero error with bounded E(latency)! Danger: new fragilities!Erasure
- 13. Two opposite views of complexityPhysics:Pattern formation by
- 14. Two opposite views of lifePhysics:If you are
- 15. NPP (Number partitioning problem)A “classic” NP complete problemThe “simplest” hard problem
- 16. 501001502002503002468101214160Example
- 17. 50100150200250300246810121416|77+65-62-59-31|= min=10max=294 = |77+65+62+59+31|140 = |77-65-62-59-31|0Scalable algorithms?
- 18. 7765625931 62 59 31625931 31 123112593101234050100 59 3131311014212121 38020413921BranchandBound
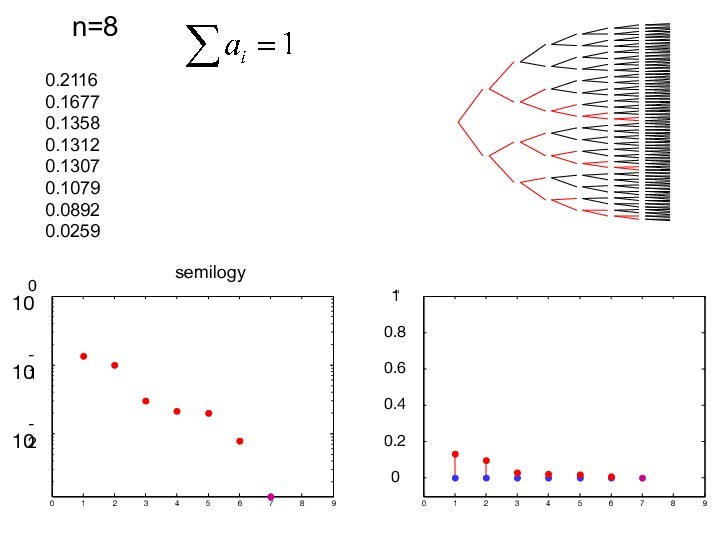
- 19. 012345678900.20.40.60.81 0.2116 0.1677 0.1358
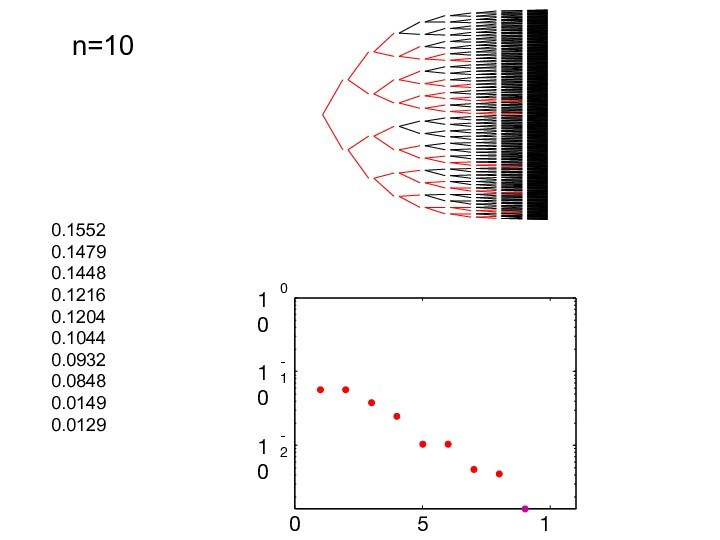
- 20. 0.1552 0.1479 0.1448
- 21. 0.20900902553447 0.16372175132032 0.11474666241757
- 22. 0.11874666798309 0.11211512926647 0.11169327453340
- 23. 024681010-310-210-1100 0.16212567898594 0.14166406741328 0.13672813657519
- 24. 010020030040050000.20.40.60.8SortedUnsortedn=10
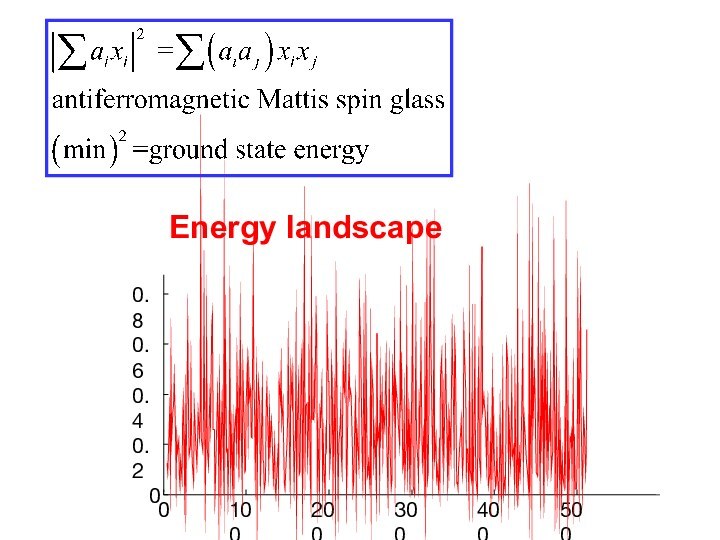
- 25. 010020030040050000.20.40.60.8Energy landscape
- 26. Mertens, Derrida, Gross & Mezard, …Large statistical physics literature
- 27. 024681010-310-210-1100n=10
- 28. 024681010-3
- 29. Why should anyone care?Computational problems in biology
- 30. Toy problem:In general:Central computational problems in biology
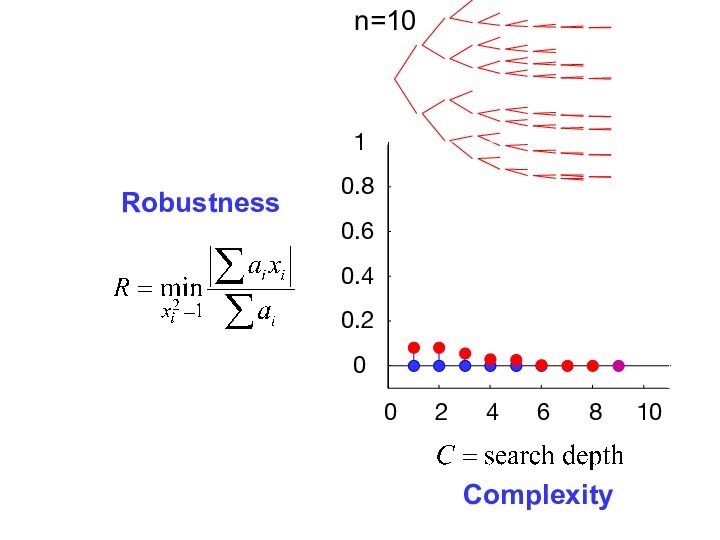
- 31. 024681000.20.40.60.81n=10RobustnessComplexity
- 32. Various levels of paranoiaexplicitly modeled uncertaintycheck for fragilities to model parameters
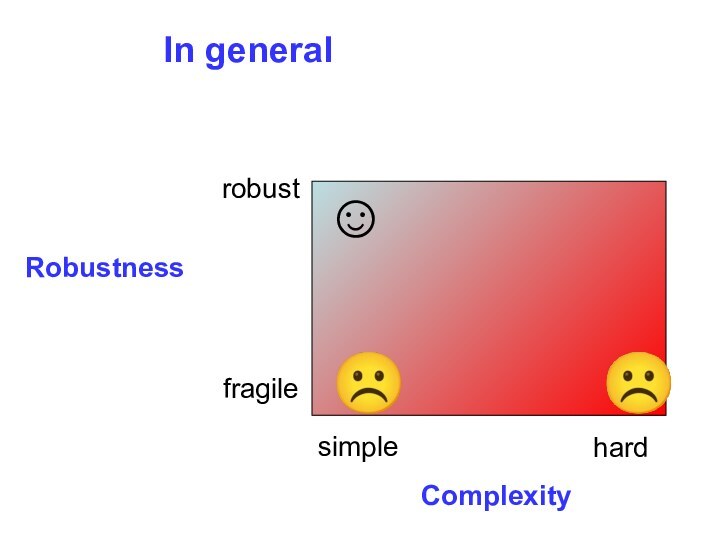
- 33. RobustnessComplexitysimplehardrobustfragile☺☹☹In general
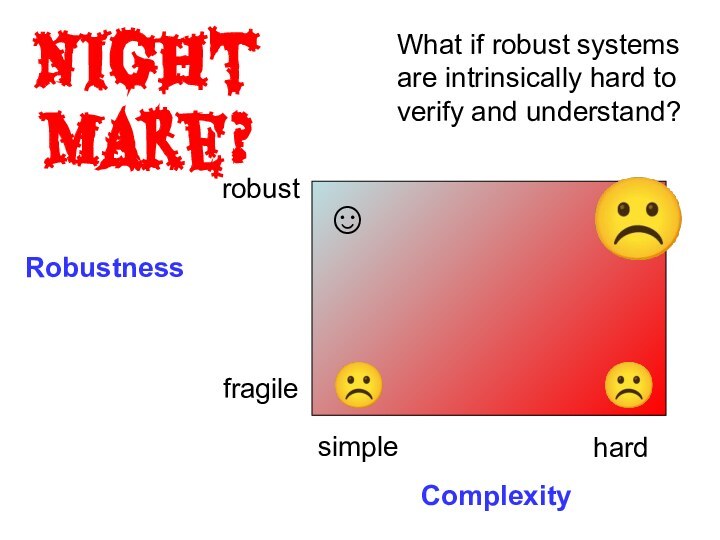
- 34. RobustnessComplexitysimplehardrobustfragile☺☹☹☹What if robust systems are intrinsically hard to verify and understand?Nightmare?
- 35. What if robust systems are intrinsically hard
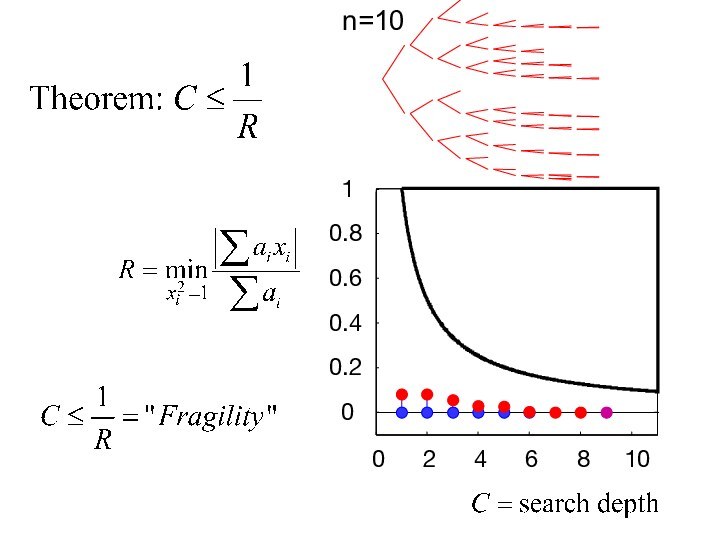
- 36. 024681000.20.40.60.81n=10
- 37. 024681000.20.40.60.81There exist example instances in all the regions permitted by the theorem.
- 38. 024681010-310-210-1100semilogy024681000.20.40.60.81n=10
- 39. 024681010-310-210-1100semilogyn=10Random problems are highly complex and extremely
- 40. 024681010-310-210-1100Random problems are highly complex and extremely
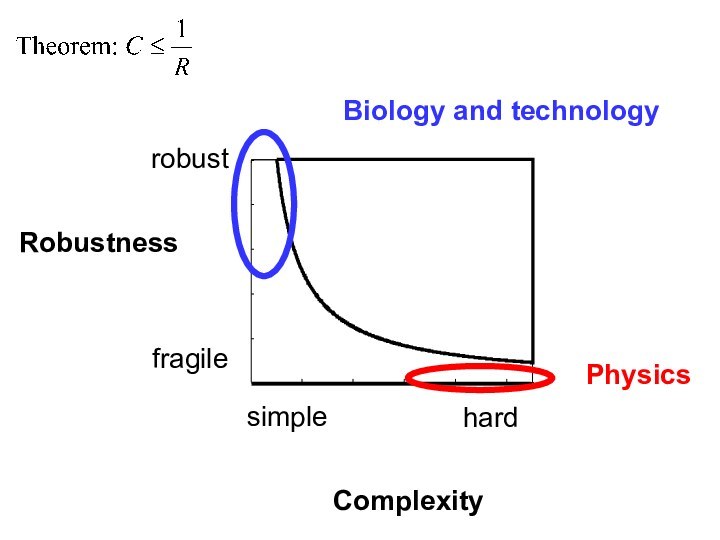
- 41. RobustnessComplexityBiology and technologyPhysicssimplehardrobustfragile
- 43. Random problemsRobust problemsRandom problems are hopelessly fragile, and it’s easy to show that:
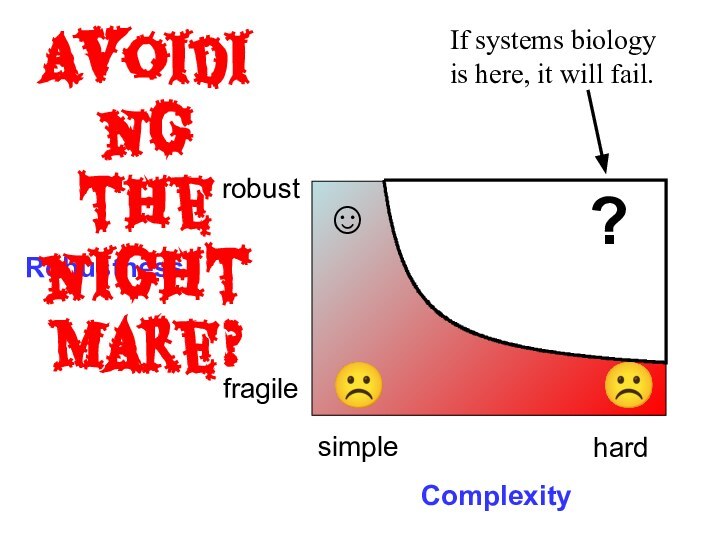
- 44. RobustnessComplexitysimplehardrobustfragile☺☹☹Avoiding the nightmare? ?If systems biology is here, it will fail.
- 45. Avoiding the nightmare? ☺☹☹☺ Must decouple organizational
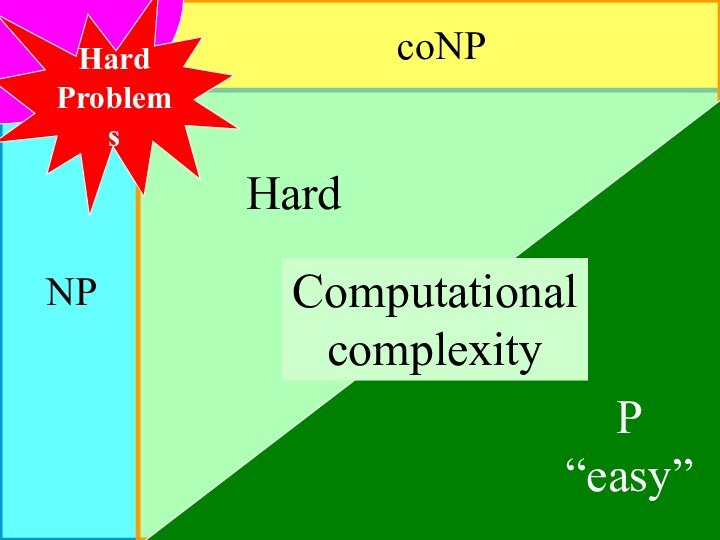
- 46. NPcoNPHard ProblemsP“easy”HardComputational complexity
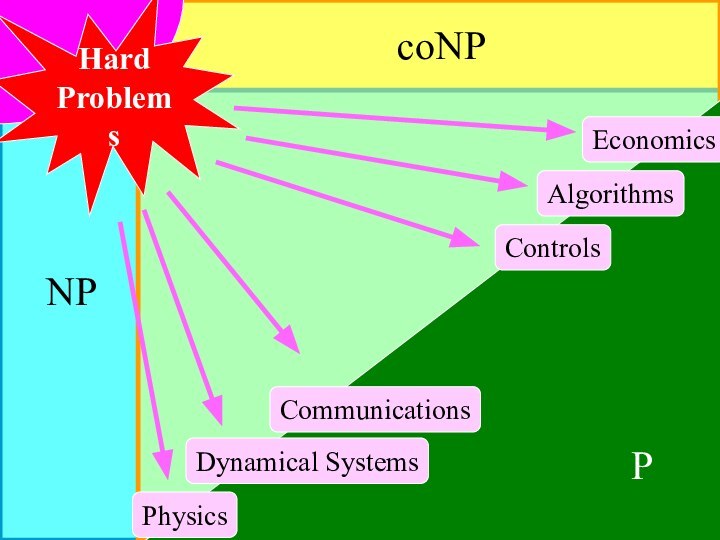
- 47. NPcoNPPControlsCommunicationsEconomicsDynamical SystemsPhysicsAlgorithmsHard Problems
- 48. PControlsCommunicationsEconomicsDynamical SystemsPhysicsAlgorithms Domain-specific assumptions Enormously successful Handcrafted
- 49. NPcoNPPControlsCommunicationsEconomicsDynamical SystemsPhysicsAlgorithmsHard ProblemsInternet
- 50. NPcoNPPControlsCommunicationsEconomicsDynamical SystemsPhysicsAlgorithmsHard ProblemsBiologyInternet
- 51. NPcoNPHard ProblemsControlsCommunicationsEconomicsDynamical SystemsPhysicsAlgorithmsGoalGoalInternetBiologyUnifiedTheory “handcrafted” theories are special cases immediate improvements new questions and answers
- 52. PControlsCommunicationsEconomicsDynamical SystemsPhysicsAlgorithms The unifying language is (new)
- 53. Скачать презентацию
- 54. Похожие презентации
























Слайд 6
Is there any hope?
What is the ultimate showstopper?
We
can make everything as robust and reliable as our
software!
Слайд 7
Robust to uncertainty in environment and components
Efficient use
of scarce resources
Scalable to large system sizes
(to do
this, it may be necessary to have high internal complexity (complicated), but we want simple, robust, verifiable external behavior, so…)
Engineering design objectives
Слайд 9
Want robustness & efficiency that is verifiably so
May
require highly complex organization and structure
Robustness, evolvability, and verifiability
are compatibleand
Tradeoff to some extent against efficiency, cost, complexity, etc.
Bottom line
Слайд 10
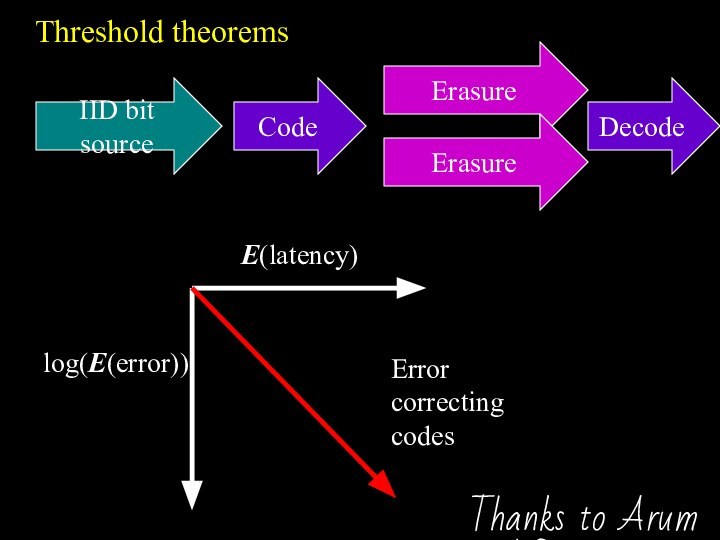
Threshold theorems
IID bit source
Erasure
Erasure
Error correcting codes
E(latency)
log(E(error))
Code
Decode
Thanks to Arum
and Ben
Слайд 11
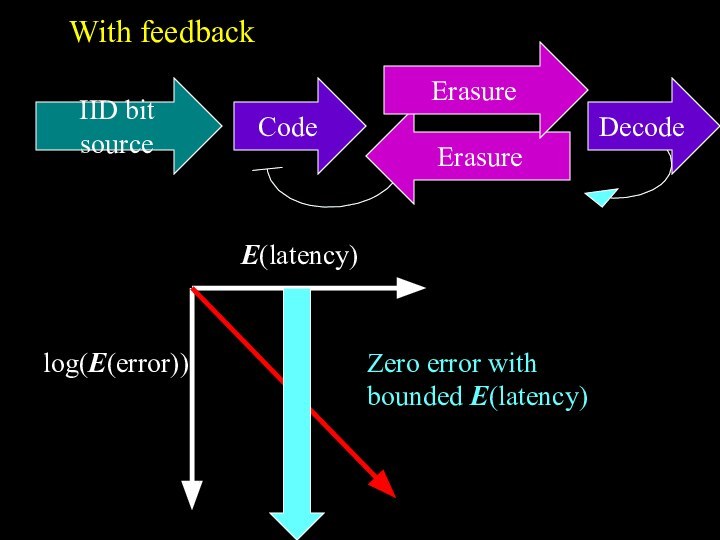
With feedback
IID bit source
Erasure
E(latency)
log(E(error))
Code
Decode
Zero error with bounded E(latency)
Erasure
Слайд 12
With feedback
IID bit source
Erasure
Code
Decode
Zero error with bounded E(latency)!
Danger: new fragilities!
Erasure
Слайд 13
Two opposite views of complexity
Physics:
Pattern formation by reaction/diffusion
Edge-of-chaos
Order
for free
Self-organized criticality
Phase transitions
Scale-free networks
Equilibrium, linear
Nonlinearity & complexity as
exoticaEngineering:
Constraints
Tradeoffs
Structure
Organization
Optimality
Robustness/fragility
Verification
Far from equilibrium
Nonlinearity & complexity as tool
Слайд 14
Two opposite views of life
Physics:
If you are dead,
you are likely to stay that way
Engineering:
If you are
alive, it is very easy to kill youThe bad news (unfortunately):
Robustness is less fungible with other features than you think.
The good news (hopefully):
If we can identify our fragilities, we can
verify that we are otherwise robust
and keep ourselves that way
Слайд 15
NPP (Number partitioning problem)
A “classic” NP complete problem
The
“simplest” hard problem
Слайд 17
50
100
150
200
250
300
2
4
6
8
10
12
14
16
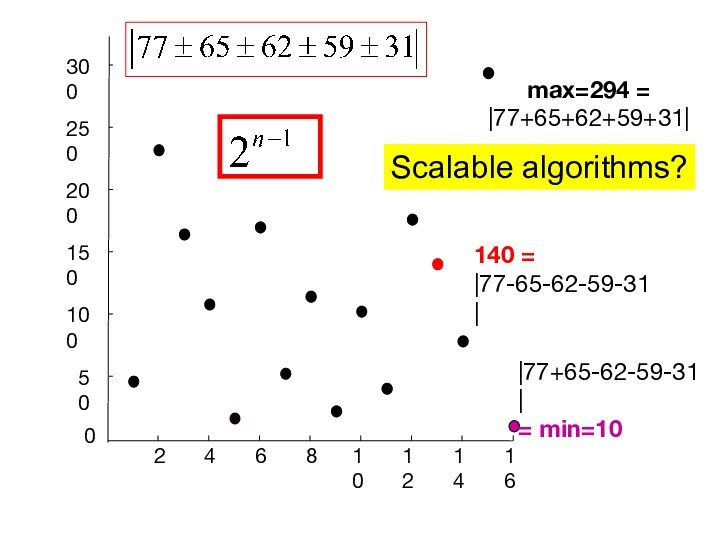
|77+65-62-59-31|
= min=10
max=294 =
|77+65+62+59+31|
140 =
|77-65-62-59-31|
0
Scalable algorithms?
Слайд 18
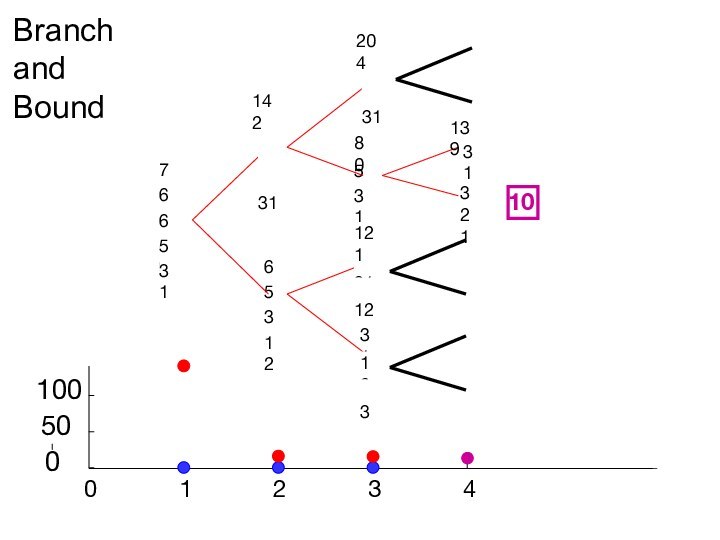
77
65
62
59
31
62
59
31
62
59
31
31
12
31
12
59
31
0
1
2
3
4
0
50
100
59
31
31
31
10
142
12
121
3
80
204
139
21
Branch
and
Bound
Слайд 21
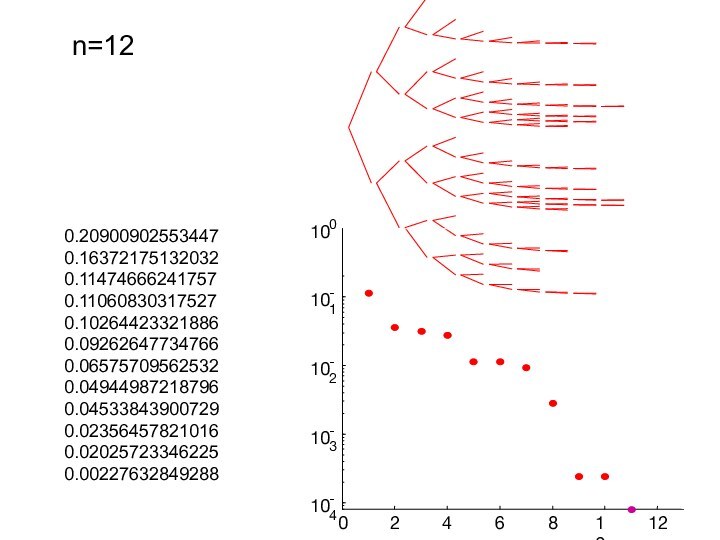
0.20900902553447
0.16372175132032
0.11474666241757
0.11060830317527
0.10264423321886
0.09262647734766
0.06575709562532
0.04944987218796
0.045338439007290.02356457821016
0.02025723346225
0.00227632849288
n=12
Слайд 22
0.11874666798309
0.11211512926647
0.11169327453340
0.11095064177068
0.09412186438521
0.08685317462754
0.08118017281551
0.06766995122518
0.057185233601140.03754549903682
0.03586488042322
0.03254947795691
0.01521112174069
0.01506074475625
0.01423812298937
0.00901404288853
n=16
Why so hard?
Still exponentially bad.
Слайд 23
0
2
4
6
8
10
10
-3
10
-2
10
-1
10
0
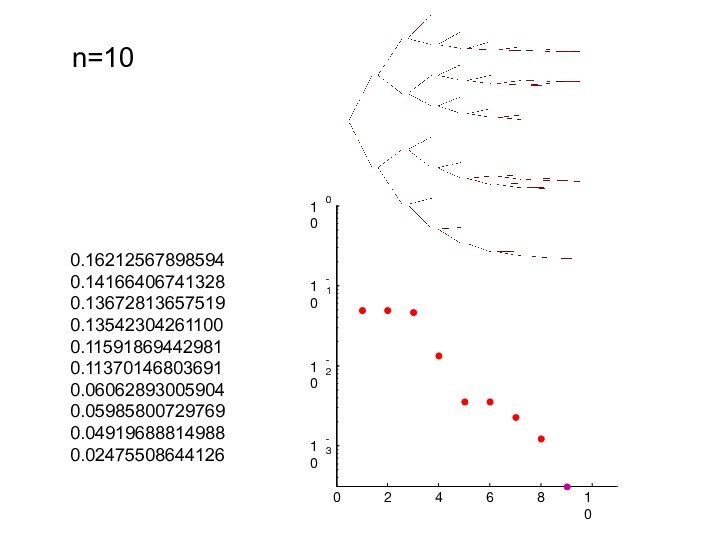
0.16212567898594
0.14166406741328
0.13672813657519
0.13542304261100
0.11591869442981
0.11370146803691
0.06062893005904
0.05985800729769
0.049196888149880.02475508644126
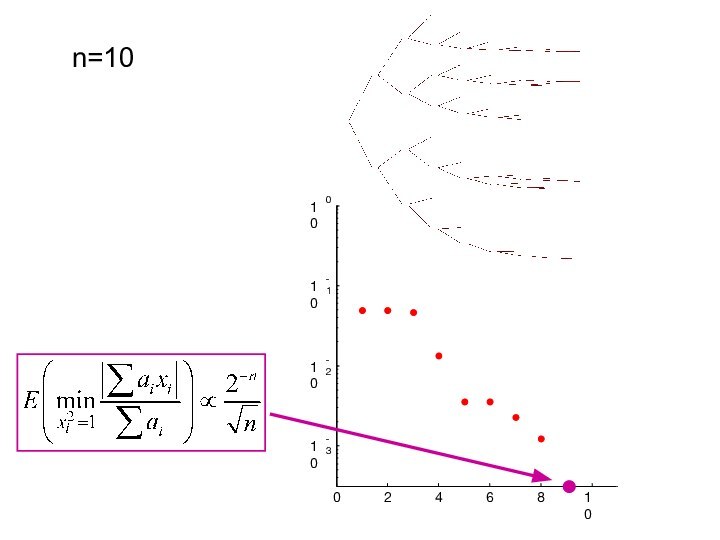
n=10
Слайд 29
Why should anyone care?
Computational problems in biology and
advanced technologies are even harder.
If we can’t do this
“simple” problem, what hope is there for scalability of computational methods to large networks?Is there some other reason for optimism?
Слайд 30
Toy problem:
In general:
Central computational problems in biology and
advanced technologies can be written this way and are
formally “hard” (NP/coNP hard or undecidable)
Слайд 32
Various levels of paranoia
explicitly modeled uncertainty
check for fragilities
to model parameters
Слайд 34
Robustness
Complexity
simple
hard
robust
fragile
☺
☹
☹
☹
What if robust systems are intrinsically hard to
verify and understand?
Nightmare?
Слайд 35 What if robust systems are intrinsically hard to
verify and understand?
Nightmare?
Biology: We might accumulate more complete
parts lists but never “understand” how it all works.Technology: We might build increasingly complex and incomprehensible systems which will eventually fail completely yet cryptically.
Nothing in the orthodox views of complexity says this won’t happen (apparently).
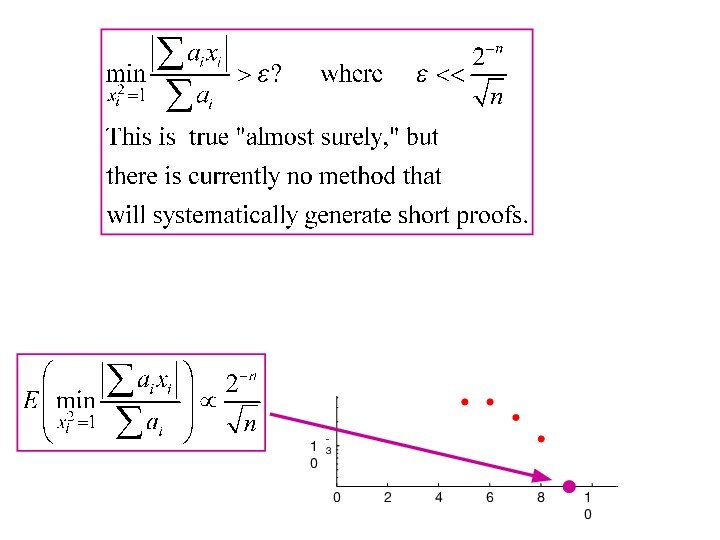
Fortunately, there is some good news.
Illustrate the “good news” in our simple problem.
Слайд 37
0
2
4
6
8
10
0
0.2
0.4
0.6
0.8
1
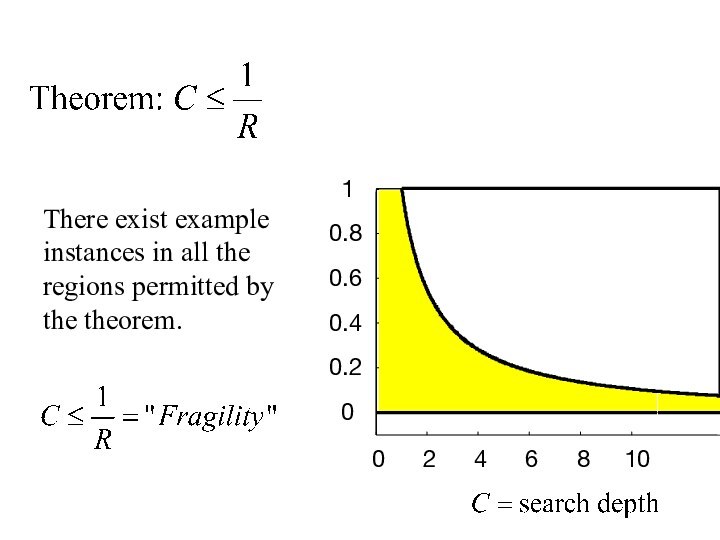
There exist example instances in all the regions
permitted by the theorem.
Слайд 39
0
2
4
6
8
10
10
-3
10
-2
10
-1
10
0
semilogy
n=10
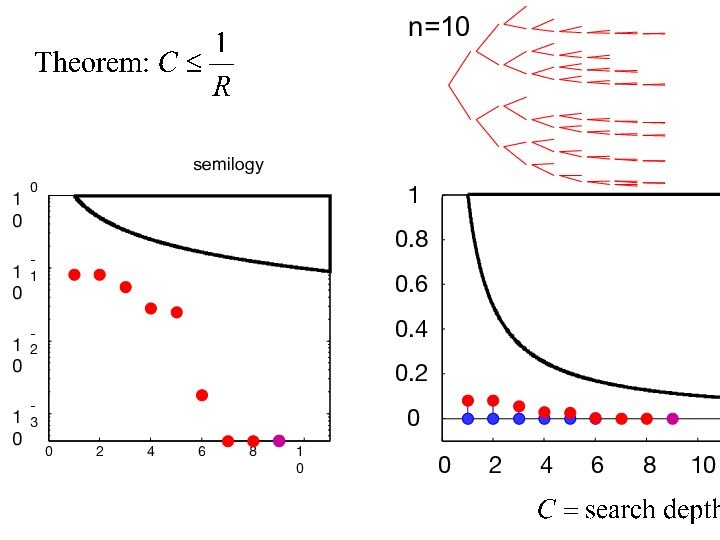
Random problems are highly complex and extremely fragile
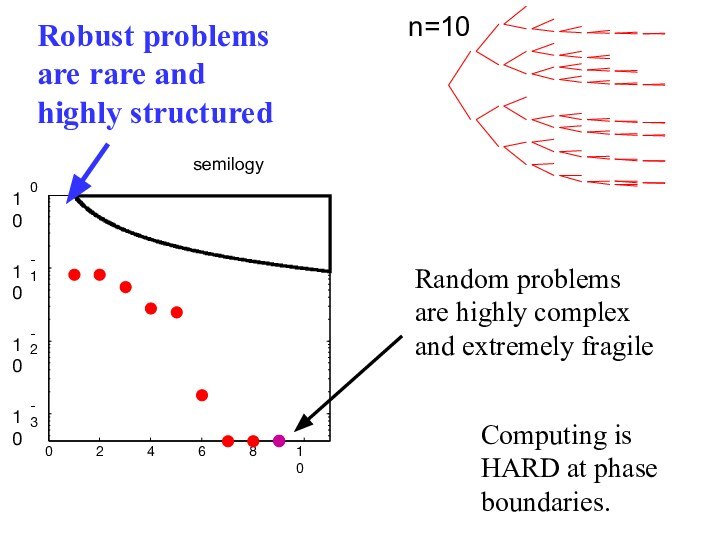
Robust
problems are rare and highly structured
Computing is HARD at
phase boundaries.
Слайд 40
0
2
4
6
8
10
10
-3
10
-2
10
-1
10
0
Random problems are highly complex and extremely fragile.
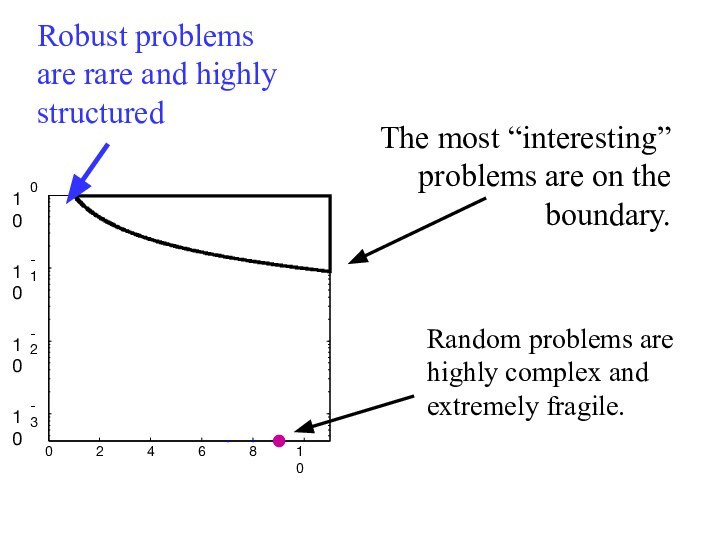
Robust
problems are rare and highly structured
The most “interesting” problems
are on the boundary.
Слайд 43
Random problems
Robust problems
Random problems are hopelessly fragile, and
it’s easy to show that:
Слайд 44
Robustness
Complexity
simple
hard
robust
fragile
☺
☹
☹
Avoiding the nightmare?
?
If systems biology is here,
it will fail.
Слайд 45
Avoiding the nightmare?
☺
☹
☹
☺
Must decouple organizational and
computational complexity
Must explicitly exploit robustness/fragility in computation
Substantial recent progress
Small tip of a huge and growing iceberg, yet…
New approach in its infancy
Слайд 48
P
Controls
Communications
Economics
Dynamical Systems
Physics
Algorithms
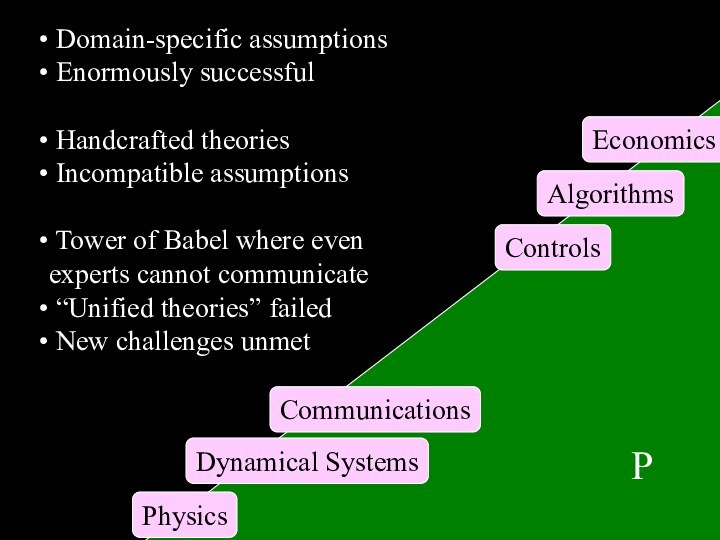
Domain-specific assumptions
Enormously successful
Handcrafted theories
Incompatible assumptions
Tower of Babel where even experts cannot
communicate“Unified theories” failed
New challenges unmet
Слайд 49
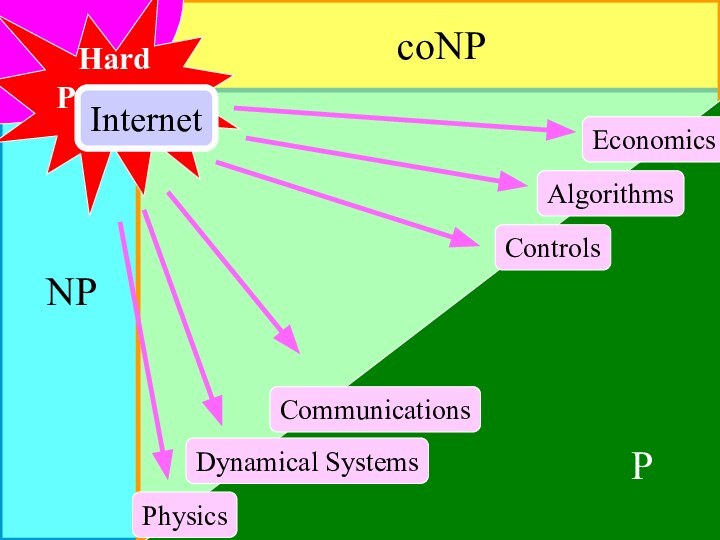
NP
coNP
P
Controls
Communications
Economics
Dynamical Systems
Physics
Algorithms
Hard
Problems
Internet
Слайд 50
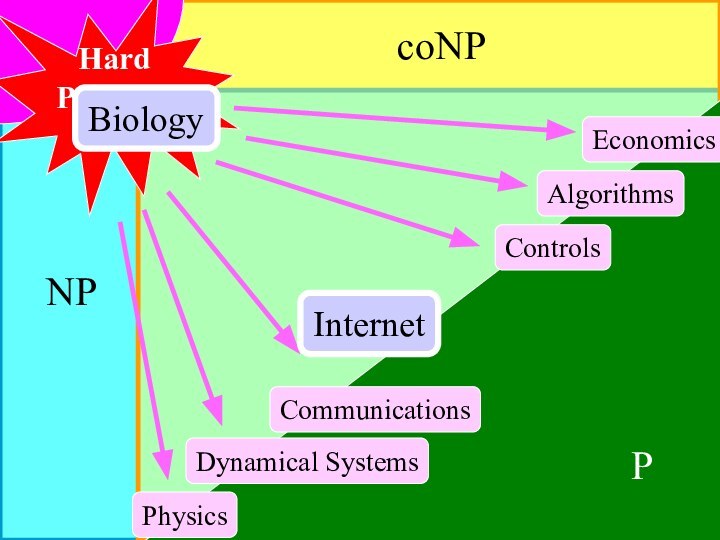
NP
coNP
P
Controls
Communications
Economics
Dynamical Systems
Physics
Algorithms
Hard
Problems
Biology
Internet
Слайд 51
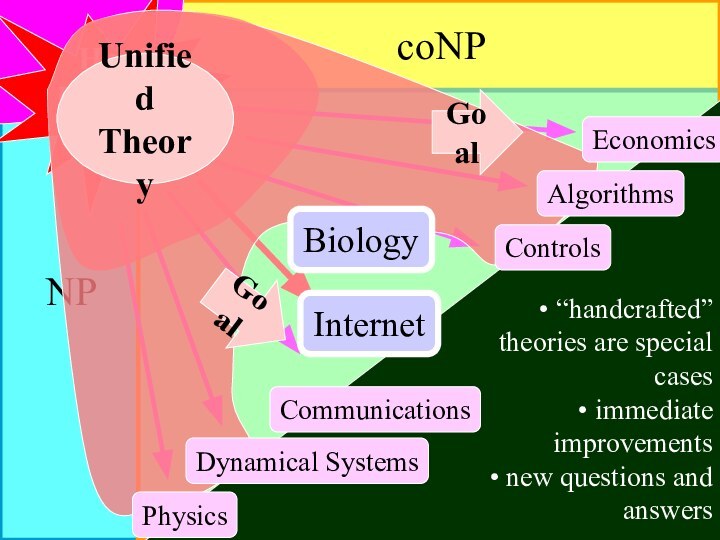
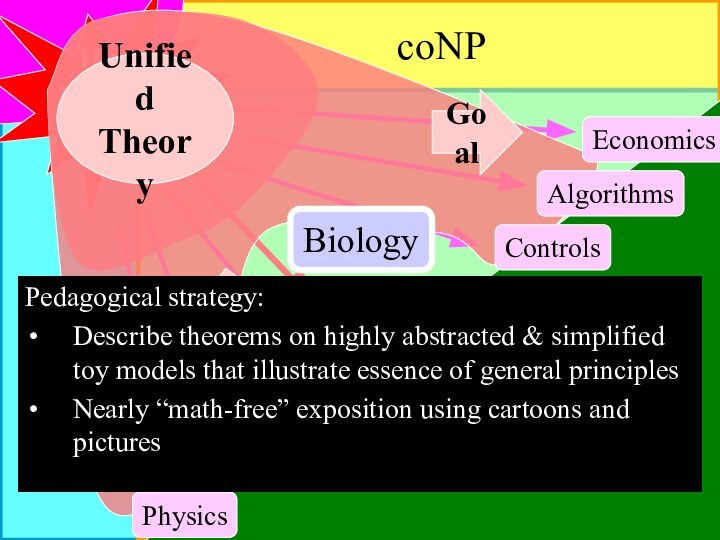
NP
coNP
Hard
Problems
Controls
Communications
Economics
Dynamical Systems
Physics
Algorithms
Goal
Goal
Internet
Biology
Unified
Theory
“handcrafted” theories are special cases
immediate improvements
new questions and answers
Слайд 52
P
Controls
Communications
Economics
Dynamical Systems
Physics
Algorithms
The unifying language is (new) mathematics
Tried to describe one important idea using simplest example
and minimal mathJust the beginning, but promising foundation for ASE?
Internet
Biology
Challenge





























