Презентация на тему Генетические алгоритмы

печатных плат, БИС, СБИС, ССБИС, изделий микро и наноэлектроники.
Принятие

решений в неопределенных и нечетких условиях.
Проблема выбора оптимальных решений в задачах науки и техники.

экстремальными функциями.

Моделирование функциями ситуаций в реальном масштабе времени.

Решение линейных

и нелинейных транспортных задач.

Решение комбинаторно логических задач искусственного интеллекта.

Решение задач принятия решений военного назначения.

процессами
селекции и генетическими преобразованиями,
протекающими в природе.
Правила образования

(синтаксис) системы ЭМ:
построения модели эволюции;
конструирования популяций;
построения ЦФ;
разработки ГО;
репродукции популяций;
рекомбинации популяций;
редукции;

Аксиомы системы ЭМ:
«Выживание сильнейших», т.е. переход решений с лучшей целевой функцией в следующую генерацию.
Размер популяции после каждой генерации остается постоянным.
Обязательное применение во всех генетических алгоритмах операторов кроссинговера и мутации.
Число копий (решений), переходящих в следующую генерацию, определяется по модифицированной формуле Холланда

процесс, посредством которого особи (альтернативные решения) некоторой популяции, имеющие

более высокое функциональное значение, получают большую возможность для воспроизведения потомков, чем «слабые» особи.

характеристики, приобретенные особью в течение жизни, наследуются его потомками.

Данная модель оказывается эффективной, когда популяция имеет сходимость в область локального оптимума.

моделирование социальных и географических
катастроф, приводящих к резкому изменению видов

и популяций.

представляется в виде схемы F1→TS→ΕΕ→F2, где F1 – исходная

проблема, TS – пробные решения, ΕΕ - устранение ошибок, F2 – новая проблема

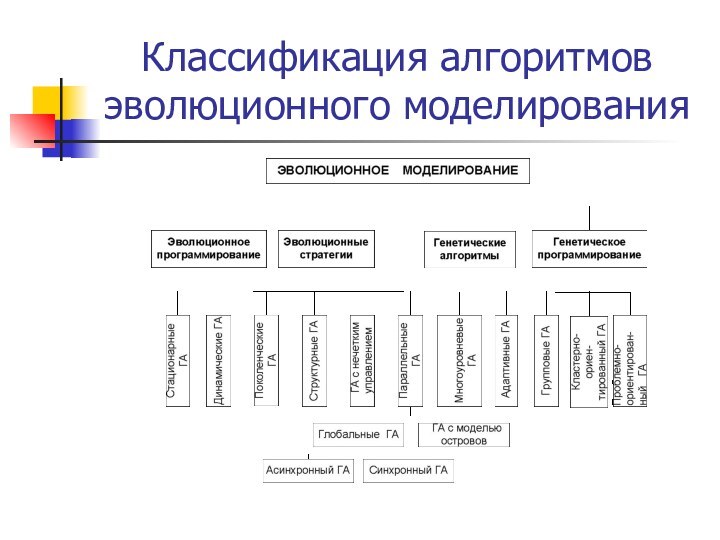
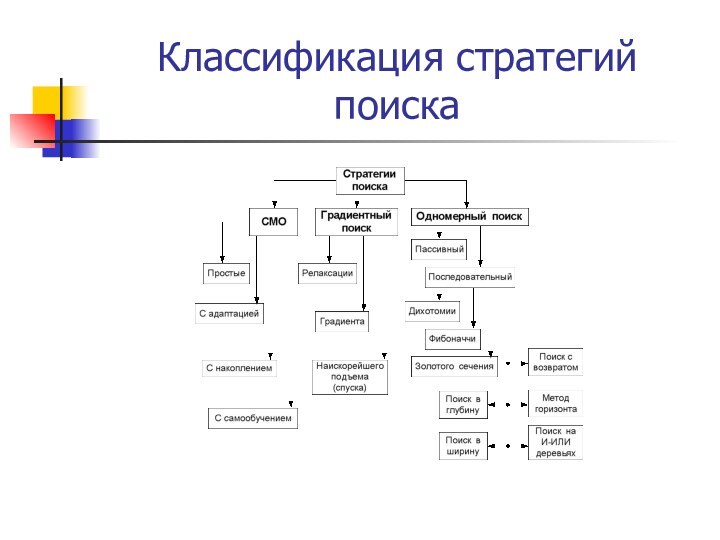
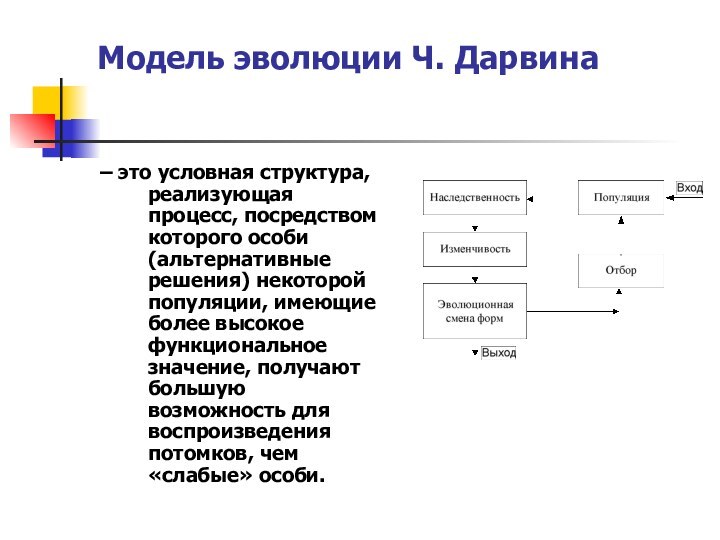
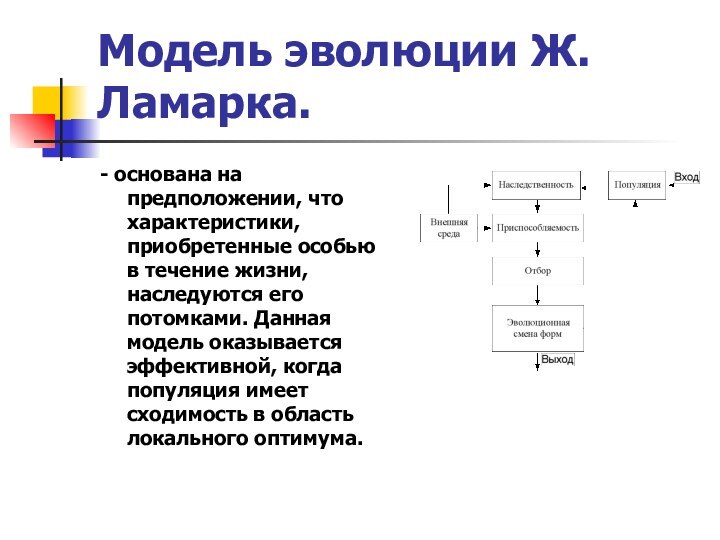
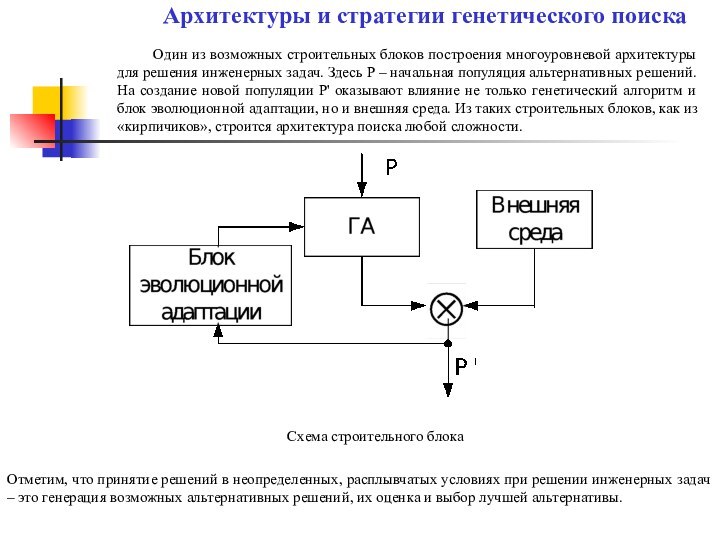
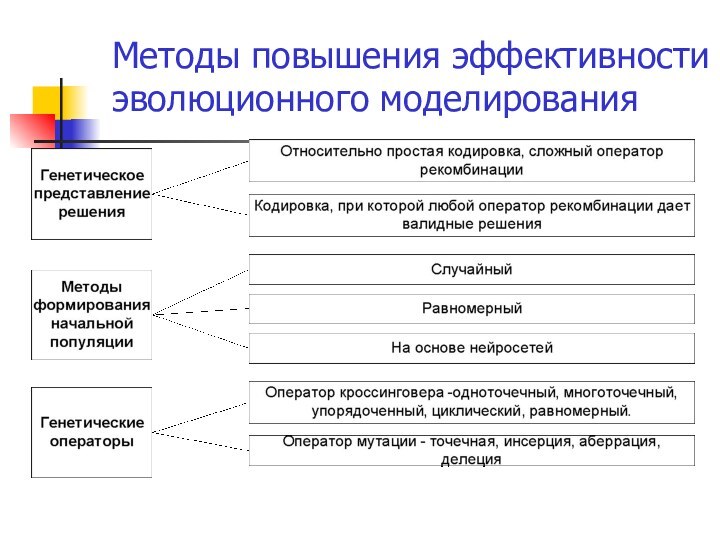
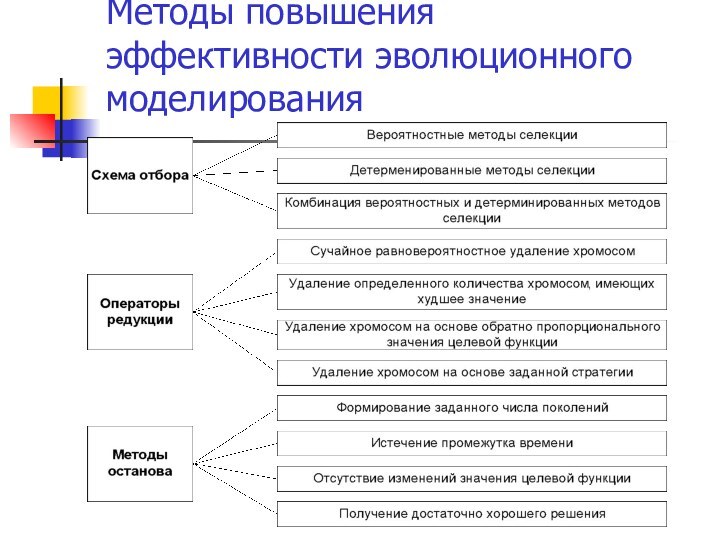
– это условная структура, реализующая иерархическую систему
гибких механизмов управления, в которых мутация интерпретируется как метод случайных проб и ошибок, а отбор как один из способов управления с помощью устранения ошибок при взаимодействии с внешней средой.

нейтральном отборе.
Эволюция заключается в реализации последовательностей поколений.
В

результате эволюции выбирается только один вид.

интеграцию различных моделей эволюций. Условия внешней среды здесь –

не только факторы исключения неприспособленных особей из популяции, но и формирующие особенности самой модели.

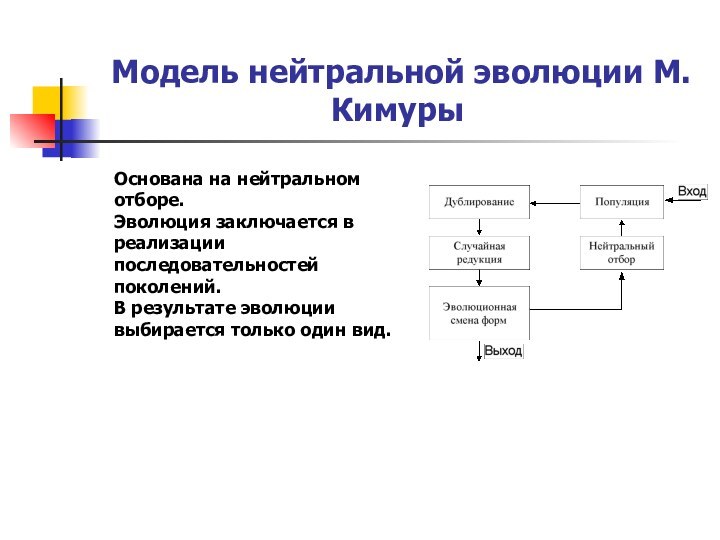
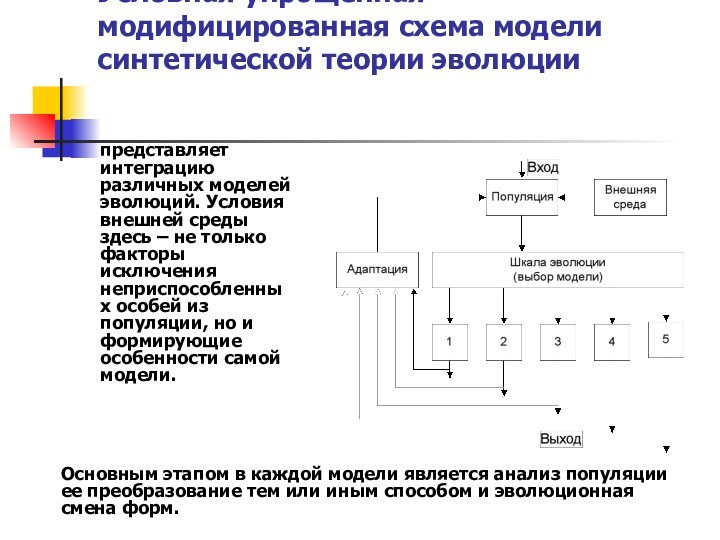
Основным этапом в каждой модели является анализ популяции ее преобразование тем или иным способом и эволюционная смена форм.

моледкулами ДНК. Здесь может быть выделено несколько подтипов рекомбинации:


регулярная

(общая) рекомбинация, представляющая собой кроссинговер, т.е. обмен гомологичными участками в различных точках гомологичных хромосом, приводящий к появлению нового сочетания сцепленных генов;
спрайт - специфическая рекомбинация, т.е. обмен генных носителей, часто разных по объему и составу, на коротких специализированных участках;
нереальная рекомбинация, реализующая негомологичные обмены. Негомологичный обмен в целом не представляет интереса, т.к. появляются нереальные решения исследуемой задачи.

Схема реализации одноточечного кроссинговера

не только в одной, но и в двух и

даже большем числе точек.

Схема двойного кроссинговера: а - до кроссинговера; б - во время кроссинговера; в - после кроссинговера

На рисунке представлена экспериментально установленная схема двойного кроссинговерамежду хромосомами (w и f).

посредством которого хромосомы (альтернативные решения), имеющие более высокое значение

ЦФ (с «лучшими» признаками), получают большую возможность для воспроизводства (репродукции) потомков, чем «худшие» хромосомы.

Селекция на основе рулетки

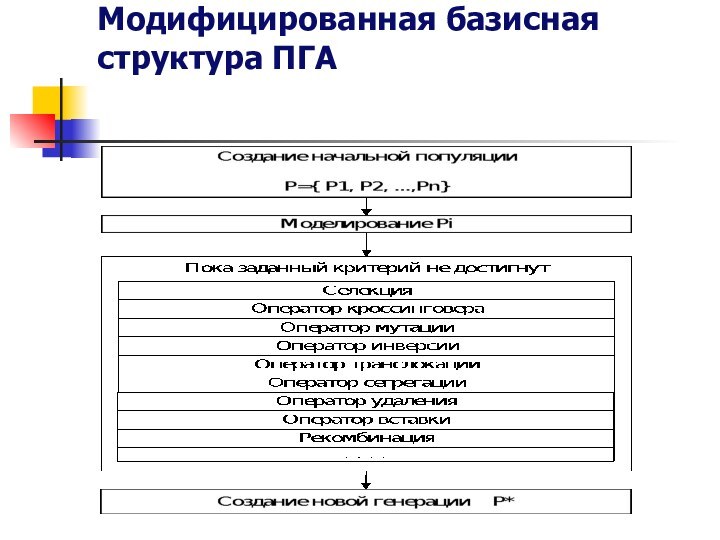
Существует большое число видов операторов репродукции. К ним относятся: селекция на основе рулетки,селекция на основе заданной шкалы, элитная селекция , турнирная селекция.

180 градусов. Инвертированный участок при нечетной длине хромосомы включает

центральный ген (перецентрическая инверсия) или не включает его при четной длине хромосомы (парацентрическая).

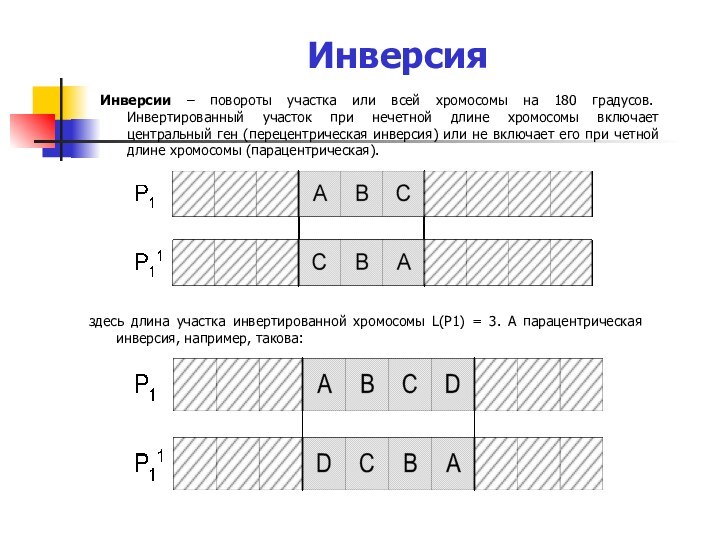
здесь длина участка инвертированной хромосомы L(P1) = 3. А парацентрическая инверсия, например, такова:

происходит редкими и быстрыми толчками.
Модели и архитектуры эволюции
Структура

макроэволюции

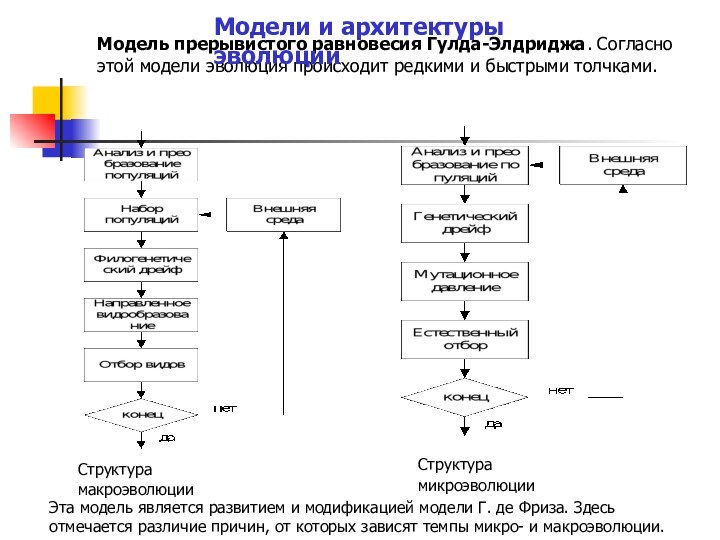
Структура микроэволюции

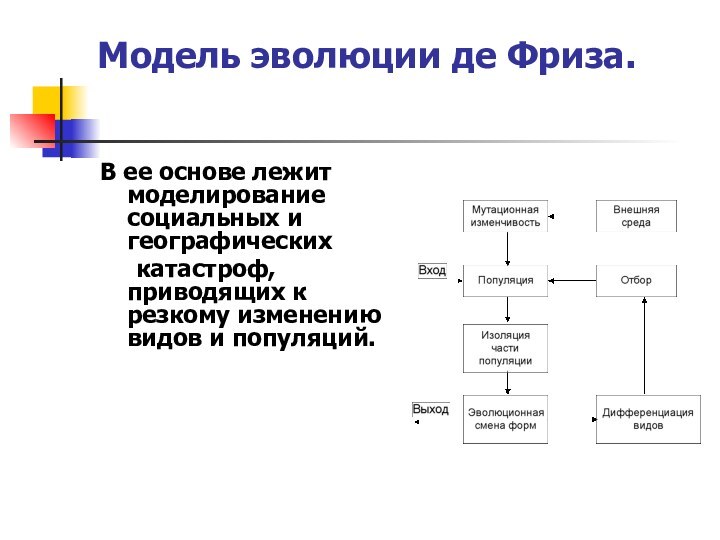
Эта модель является развитием и модификацией модели Г. де Фриза. Здесь отмечается различие причин, от которых зависят темпы микро- и макроэволюции.

в том, чтобы:
абстрактно и формально объяснить адаптацию процессов в

ЕС и интеллектуальной ИС;
моделировать естественные эволюционные процессы для эффективного решения оптимизационных задач науки и техники.
В настоящее время используется новая парадигма решений оптимизационных задач на основе генетических алгоритмов и их различных модификаций. Генетические алгоритмы осуществляют поиск баланса между эффективностью и качеством решений за счет «выживания сильнейших альтернативных решений», в неопределенных и нечетких условиях.
Генетические алгоритмы отличаются от других оптимизационных и поисковых процедур следующим:
работают в основном не с параметрами задачи, а с закодированным множеством параметров;
осуществляют поиск не путем улучшения одного решения, а путем использования сразу нескольких альтернатив на заданном множестве решений;
используют целевую функцию (ЦФ), а не ее различные приращения для оценки качества принятия решений;
применяют не детерминированные, а вероятностные правила анализа оптимизационных задач.

при решении практических задач. Одно из них – это

адаптация к изменяющейся окружающей среде.
При использовании традиционных методов все вычисления приходится начинать заново, что приводит к большим затратам машинного времени. При эволюционном подходе популяцию можно анализировать, дополнять и видоизменять применительно к изменяющимся условиям.
Преимущество генетических алгоритмов для решения задач состоит в способности быстрой генерации достаточно хороших решений.
При решении практических задач с использованием генетических алгоритмов обычно выполняют четыре предварительных этапа:
выбор способа представления решения;
разработка операторов случайных изменений;
определение способов «выживания» решений;
создание начальной популяции альтернативных решений.

степень реализации запланированных действий алгоритма и достижение требуемых значений

целевой функции. Эффективность во многом определяется структурой и составом начальной популяции.
При создании начального множества решений происходит формирование популяции на основе четырех основных принципов:
«одеяла» – генерируется полная популяция, включающая все возможные решения в некоторой заданной области;
«дробовика» – подразумевает случайный выбор альтернатив из всей области решений данной задачи.
«фокусировки» – реализует случайный выбор допустимых альтернатив из заданной области решений данной задачи.
Комбинирования – состоит в различных совместных реализациях первых трех принципов.

кроссинговера определяется так называемая точка оператора кроссинговера, или разрезающая

точка оператора кроссинговера, которая обычно определяется случайно. Эта точка определяет место в двух хромосомах, где они должны быть «разрезаны».

Одноточечный оператор кроссинговера

Одноточечный оператор кроссинговера выполняется в три этапа:
Две хромосомы A = а1, а2,.., аL и B = a′1, a′2,.., a′L выбираются случайно из текущей популяции.
Число k выбирается из {1,2,...,L-1} также случайно. Здесь L - длина хромосомы, k - точка оператора кроссинговера (номер, значение или код гена, после которого выполняется разрез хромосомы).
Две новые хромосомы формируются из A и B путем перестановок элементов согласно правилу

Р1 : 1 1 | 1 1 1
Р2 : 0 0 | 0 0 0
________________
Р'1 : 1 1 | 0 0 0
Р'2 : 0 0 | 1 1 1

две точки оператора кроссинговера, и хромосомы обмениваются участками, расположенными

между двумя точками оператора кроссинговера.

Р1 : 1 1 1 | 0 1 | 0 0
Р2 : 0 0 0 | 1 1 | 1 0
____________________
Р'1 : 1 1 1 | 1 1 | 0 0
Р'2 : 0 0 0 | 0 1 | 1 0

Пример двухточечного оператора кроссинговера

Развитием двухточечного оператора кроссинговера является многоточечный оператор кроссинговера или N-точечный оператор кроссинговера. Многоточечный оператор кроссинговера выполняется аналогично двухточечному оператору кроссиновера, хотя большое число «разрезающих» точек может привести к потере «хороших» родительских свойств.

Р1 : 1 | 1 1 |0 1 | 0 0
Р2 : 0 |0 0 |1 0 | 1 1
____________________
Р'1 : 1| 0 0 | 0 1 | 1 1
Р'2 : 0 |1 1 | 1 0 | 0 0

Пример трехточечного оператора кроссинговера

универсальный оператор кроссинговера определяют двоичную маску, длина которой равна

длине заданных хромосом. Первый потомок получается сложением первого родителя с маской на основе следующих правил (0+0=0, 0+1=1, 1+1=0). Второй потомок получается аналогичным образом. Для каждого элемента в Р1, Р2 гены меняются.

Р1 : 0 1 1 0 0 1
P2 : 0 1 0 1 1 1
________________
0 1 1 0 1 0 − маска
_______________
P'1 : 0 0 0 0 1 1
P'2 : 0 0 1 1 0 1

Универсальный оператор кроссинговера

Маска может быть задана или выбирается случайно с заданной вероятностью или на основе генератора случайных чисел. При этом чередование 0 и 1 в маске происходит с вероятностью ≈50%. В некоторых случаях используется параметризированный универсальный оператор кроссинговера, где маска может выбираться с вероятностью для 1 или 0 выше, чем 50%. Такой вид маски эффективен, когда хромосомы кодируются в двоичном алфавите.

это языковая конструкция, позволяющая на основе преобразования родительской хромосомы

(или ее части) создавать хромосому потомка.

Простейшим оператором мутации является одноточечный. При его реализации случайно выбирают ген в родительской хромосоме и, обменивая его на рядом расположенный ген, получают хромосому потомка.

Р1 : 0 1 1 | 0 1 1
Р'1 : 0 1 0 | 1 1 1

При реализации двухточечного оператора мутации случайным или направленным образом выбираются две точки разреза. Затем производится перестановка генов между собой, расположенных справа от точек разреза.

Р : A | B C D | E F
P' : A E С D B F

Одноточечный оператор мутации

Р1 – родительская хромосома, а Р'1 – хромосома-потомок после применения одноточечного оператора мутации

Двухточечный оператор мутации

Р1 – родительская хромосома, а Р'1 – хромосома-потомок после применения двухточечного оператора мутации

быть доведена до N блоков. Причем N − 1

блоков могут параллельно осуществлять эволюционную адаптацию и через блоки миграции обмениваться лучшими представителями решений. Последний блок собирает лучшие решения, может окончить результат работы или продолжить эволюционный поиск.

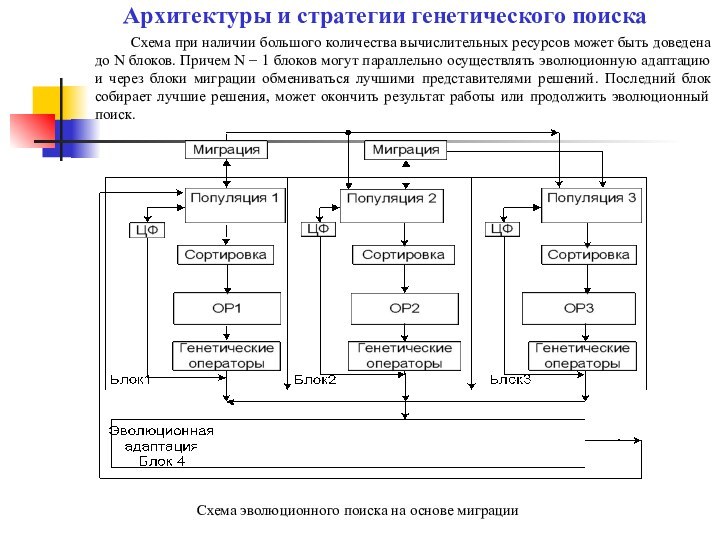
Схема эволюционного поиска на основе миграции

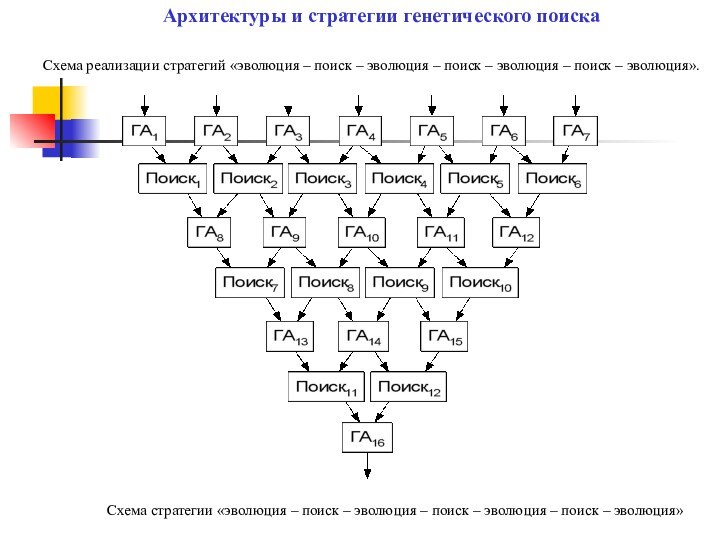
Архитектуры и стратегии генетического поиска

считалось в древних учениях, обладают внутренней красотой и гармонией.

Использовано отношение вход-выход «1 – многие». Отметим, что здесь могут быть использованы и другие отношения вход-выход: «1 – 1»; «многие – 1»; «многие – многие». Эффективность таких отношений проверяется экспериментально. Под эффективностью понимается степень реализации запланированной деятельности и достижения запланированных результатов.

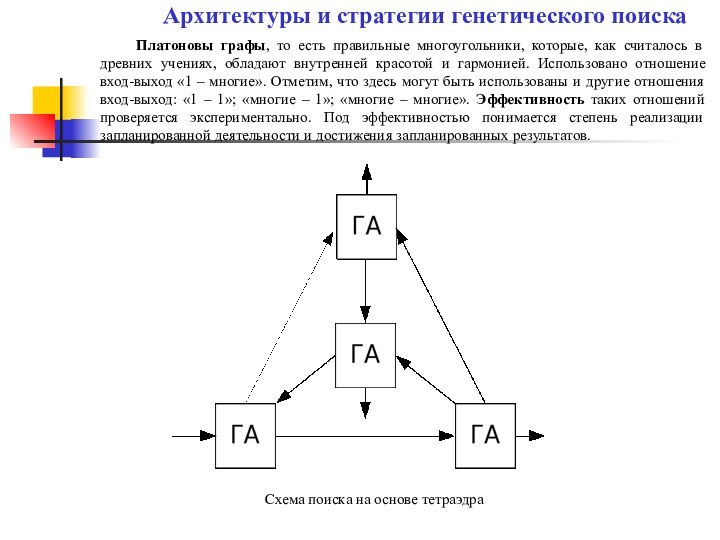
Схема поиска на основе тетраэдра

Архитектуры и стратегии генетического поиска

основе Платоновых графов додекаэдра. Отметим, что здесь могут быть

использованы и другие отношения вход-выход: «1 – 1»; «многие – 1»; «многие – многие».

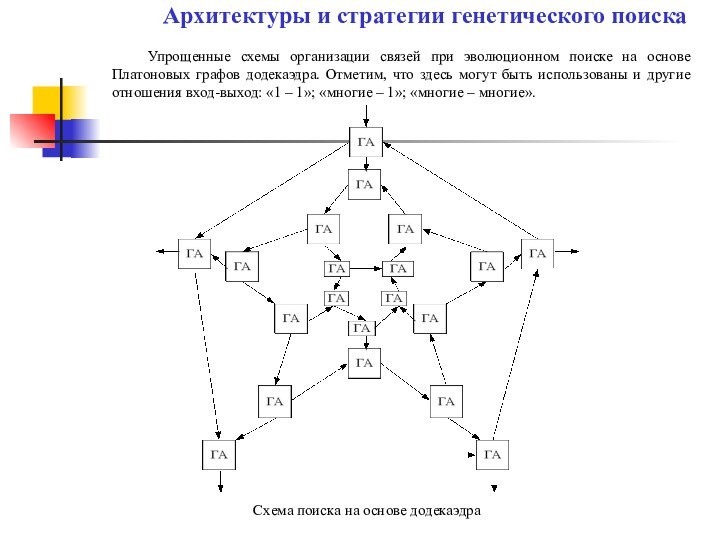
Архитектуры и стратегии генетического поиска

Схема поиска на основе додекаэдра

Здесь основным является первый блок, в котором осуществляется реализация

ГА, генерация новых решений, определение значения ЦФ и использование предыдущих решений для генерации лучших результатов. Второй блок позволяет использовать «историю» предыдущих решений для генерации лучшего множества параметров. В третьем блоке генерируется новое множество оптимизационных параметров.

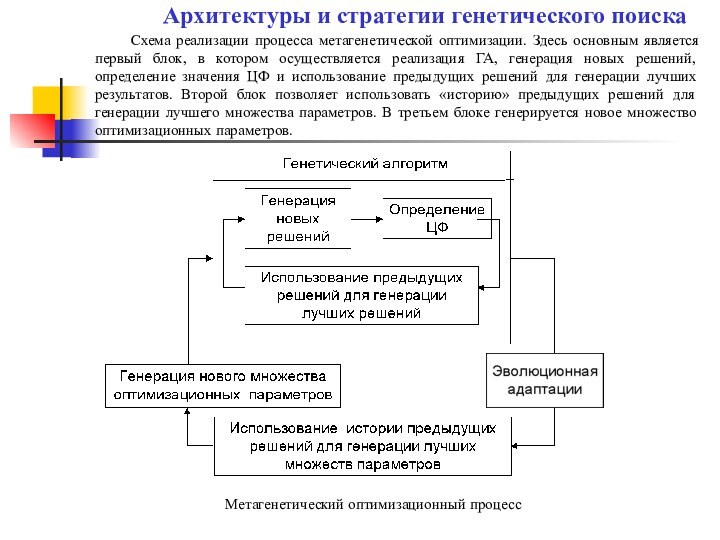
Архитектуры и стратегии генетического поиска

а несколько альтернативных решений. Причем в зависимости от сложности

перерабатываемой информации исходные решения могут быть получены на основе стохастических, детерминированных или комбинированных алгоритмов.

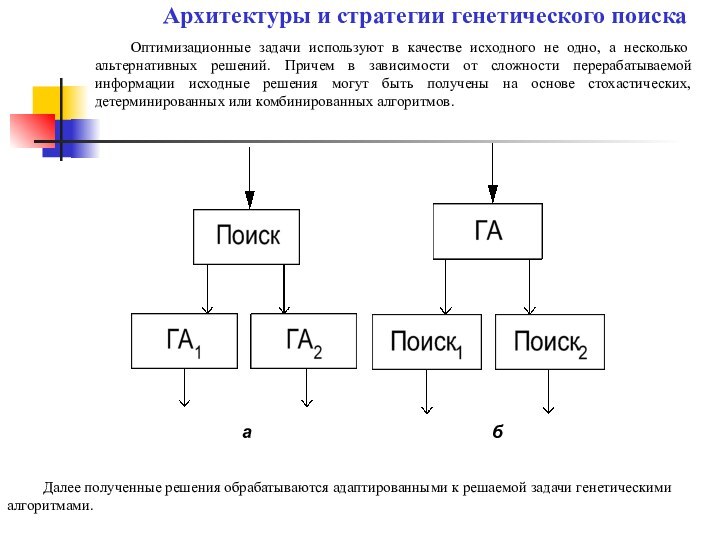
Далее полученные решения обрабатываются адаптированными к решаемой задачи генетическими алгоритмами.

а

б

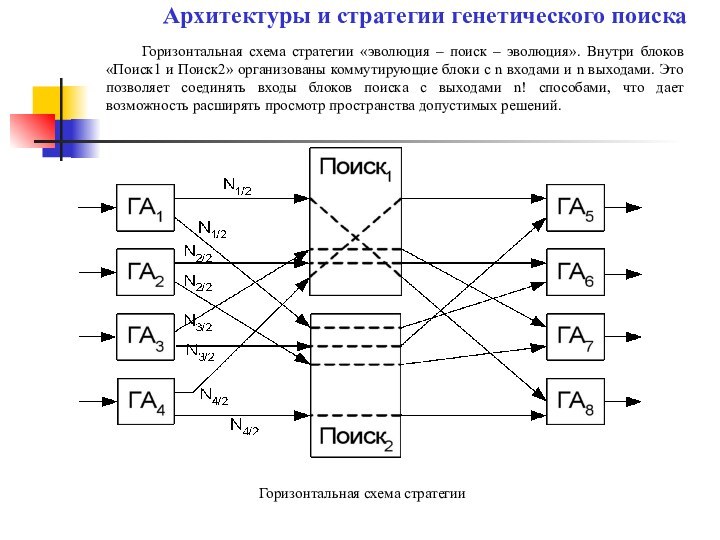
Архитектуры и стратегии генетического поиска

Внутри блоков «Поиск1 и Поиск2» организованы коммутирующие блоки с

n входами и n выходами. Это позволяет соединять входы блоков поиска с выходами n! способами, что дает возможность расширять просмотр пространства допустимых решений.

Горизонтальная схема стратегии

Архитектуры и стратегии генетического поиска

– поиск – эволюция – поиск – эволюция».
Схема стратегии

«эволюция – поиск – эволюция – поиск – эволюция – поиск – эволюция»

Архитектуры и стратегии генетического поиска

для решения инженерных задач. Здесь Р – начальная популяция

альтернативных решений. На создание новой популяции Р' оказывают влияние не только генетический алгоритм и блок эволюционной адаптации, но и внешняя среда. Из таких строительных блоков, как из «кирпичиков», строится архитектура поиска любой сложности.

Схема строительного блока

Отметим, что принятие решений в неопределенных, расплывчатых условиях при решении инженерных задач – это генерация возможных альтернативных решений, их оценка и выбор лучшей альтернативы.

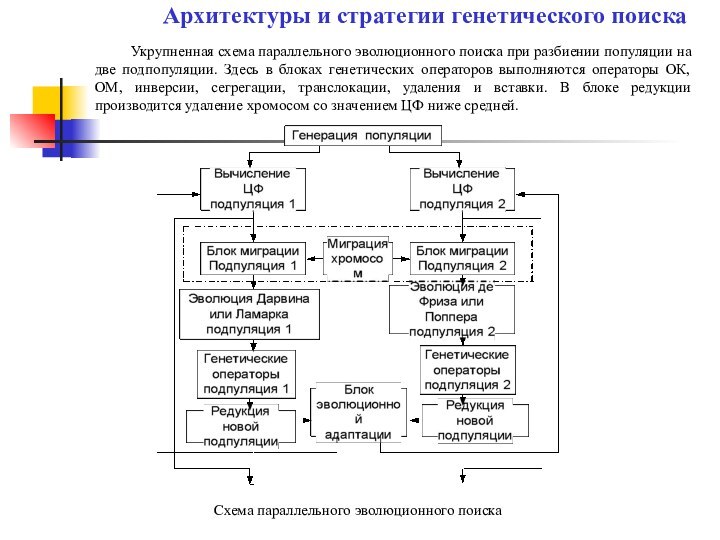
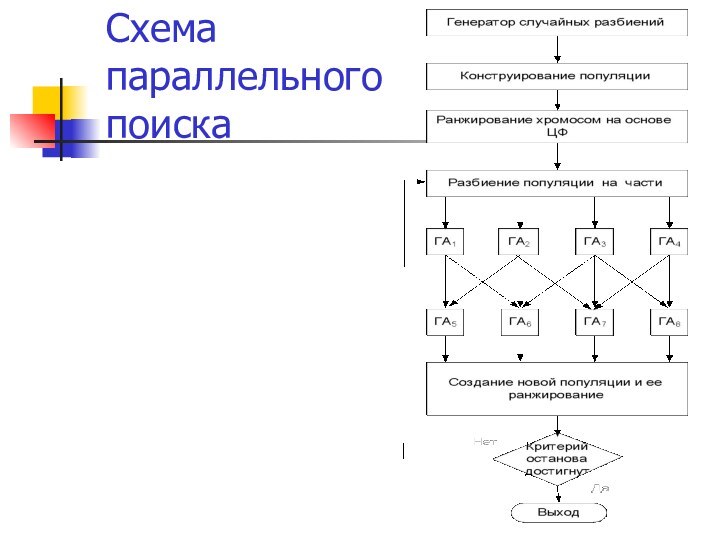
Архитектуры и стратегии генетического поиска

поиска при разбиении популяции на две подпопуляции. Здесь в

блоках генетических операторов выполняются операторы ОК, ОМ, инверсии, сегрегации, транслокации, удаления и вставки. В блоке редукции производится удаление хромосом со значением ЦФ ниже средней.

Архитектуры и стратегии генетического поиска

алгоритмах значение целевой функции альтернативного решения не сводится к

сумме целевых функций частичных решений.

Принцип дополнительности. При решении оптимизационных задач возникает необходимость использования различных не совместимых и взаимодополняющих моделей эволюции и исходных объектов.

Принцип неточности. При росте сложности анализируемой задачи уменьшается возможность построения точной модели.

Принцип управления неопределенностью. Необходимо вводить различные виды неопределенности в генетические алгоритмы.

Принцип соответствия. Язык описания исходной задачи должен соответствовать наличию имеющейся о ней информации.

Принцип разнообразия путей развития. Реализация генетических алгоритмов многовариантна и альтернативна. Существует много путей эволюции. Основная задача выбрать путь, приводящий к получению оптимального решения.

«Хаос не только разрушителен, но и конструктивен», т.е. в

хаосе области допустимых решений обязательно содержится порядок, определяющий искомое решение.

Принцип совместимости и разделительности. Процесс эволюции носит поступательный, пульсирующий или комбинированный характер. Поэтому модель синтетической эволюции должна сочетать все эти принципы.

Принцип иерархичности. Генетические алгоритмы могут подстраиваться сверху вниз и снизу вверх.

Принцип «Бритвы Оккама». Нежелательно увеличивать сложность архитектуры поиска без необходимости.
Бритва Оккама – принцип выдвинутый английским философом XIV века Уильямом Оккамом «Понятия, не сводимые к интуитивному и опытному знанию следует исключать из науки»

Принцип гомеостаза. Генетические алгоритмы конструируются таким образом, что любое полученное альтернативное решение не выходило из области допустимых.

окончание

Основные принципы совместного поиска:

САПР на основе бионических и эволюционных моделей»
Специальные математические модели на

основе графов и гиперграфов для решения оптимизационных задач;
Интеллектуальные процедуры решения оптимизационных задач;
Новые стратегии моделирования различных эволюций;
Наборы правил и знаний для интеллектуальных решателей задач;
Архитектура интеллектуальной программной среды для применения методов генетической оптимизации;
Экспертные оболочки для решения оптимизационных задач;
Исследование механизмов основных генетических операторов и на их основе разработка новых модификаций алгоритмов, обеспечивающих оптимизацию структуры поиска;
Новые подходы к решению оптимизационных задач на основе стратегий «поиск – эволюция – поиск», «эволюция – поиск – эволюция»;
Новые технологии решения оптимизационных задач на основе методов агрегации фракталов;
Проблемно-ориентированные ГА, вырабатывающие решение комбинаторных задач, представленных как задачи параметрической оптимизации;
Новые подходы к решению оптимизационных задач на основе системного подхода и принципов самоорганизации и саморегулирования;
Разработка алгоритмов решения комбинаторно-логических задач на основе генетических, синергетических методов и методов самообучения адаптивных систем;
Реализация программного комплекса поддержки среды решения оптимизационных задач и управления на основе адаптивных поисковых алгоритмов. Комплекс ориентирован на работу с IBM PC, допускается также использование комплекса в корпоративной сети предприятия. Демонстрационная версия комплекса представлялась различных на научно-технических конференциях и семинарах, также на международной выставке CEBIT’98 в Ганновере (Германия), международной конференции «Искусственные интеллектуальные системы IEEE AIS’02»

использует эволюционные процедуры для одномерной упаковки произвольно заданного количества

элементов в блоки.

Программный продукт реализован в среде MS Windows на языке Borland C++ 4.5.
Среда функционирования: MS WINDOWS 98, XP, 2000.
Системные требования: Pentium 333, 128Mb RAM, + 4 Mb дискового пространства, графическое разрешение 800 Х 600 пикселей.

оптимальной 2D упаковки со связями разработан для решения проблемы

упаковки элементов СБИС. Элементом СБИС представляется в виде прямоугольника с входами/выходами, расположенными по краям.

Программный продукт оптимальной 2D упаковки со связями имеет удобный и наглядный интерфейс. Имеется встроенный редактор задач. В программе имеются три основных блока: Окно Редактора, Окно Инспектора свойств, Окно Алгоритма.
Среда функционирования: MS WINDOWS 98, XP, 2000.
Системные требования: Pentium 333, 128Mb RAM, + 4 Mb дискового пространства, графическое разрешение 800 Х 600 пикселей.

Область трассировки - канал, ограниченный двумя линейками контактов. Цель

- размещение фрагментов цепей в минимальном числе магистралей.

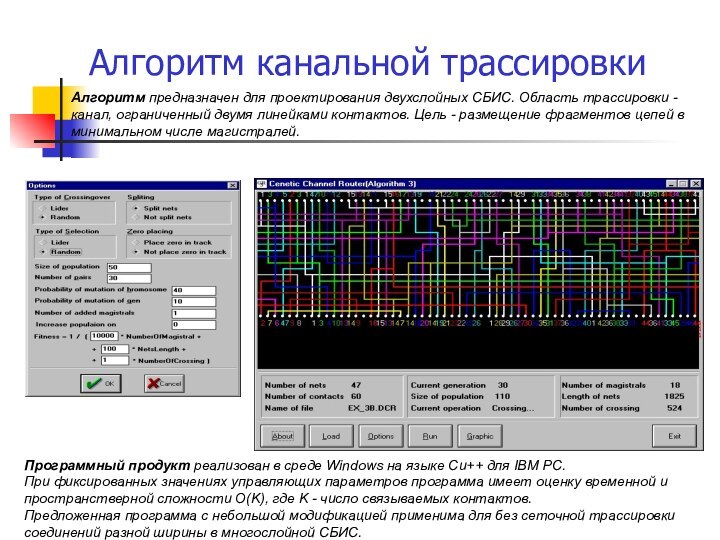
Программный продукт реализован в среде Windows на языке Си++ для IВМ РС.
При фиксированных значениях управляющих параметров программа имеет оценку временной и пространствеpной сложности О(K), где K - число связываемых контактов.
Предложенная программа с небольшой модификацией применима для без сеточной трассировки соединений разной ширины в многослойной СБИС.

упаковки со связями разработан для решения проблемы упаковки элементов,

имеющих любое количество измерений. Целью упаковки является нахождение такого легального размещения элементов, при котором объем ограничивающей прямоугольной области будет минимален.

Программный продукт N-мерной упаковки элементов со связями имеет удобный и наглядный интерфейс. Имеется встроенный редактор задач. В программе имеются три основных блока: Окно Редактора, Окно Инспектора свойств, Окно Алгоритма.
Среда функционирования: MS WINDOWS 98, XP, 2000.
Системные требования: Pentium 333, 128Mb RAM, + 4 Mb дискового пространства, графическое разрешение 800 Х 600 пикселей.

(ГАСЭС)
Алгоритм ГАСЭС позволяет решать задачу компоновки элементов СБИС по

критерию суммарного числа цепей между узлами, с учётом тепловой совместимости компонуемых элементов.

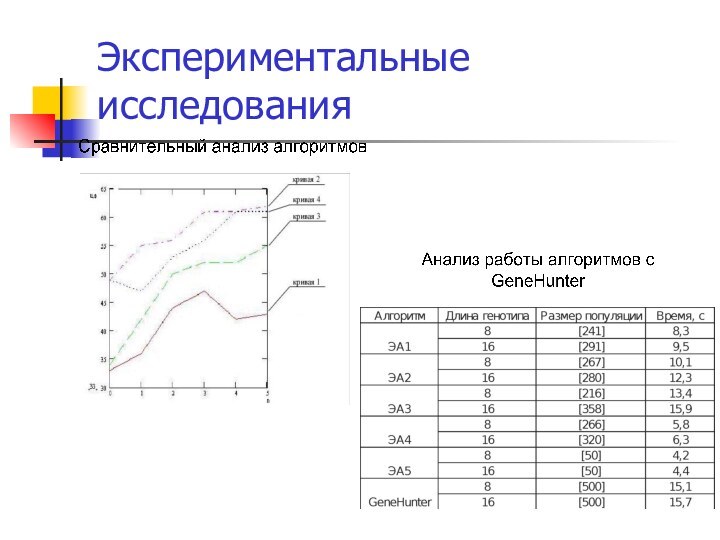
Программный продукт, позволяет проводить экспериментальные исследования в зависимости от значений основных параметров алгоритма и динамических параметров. В главном окне отображается процесс работы алгоритма и другая вспомогательная информация.
Результаты экспериментальных исследований показали, что ГАСЭС по сравнению с простым генетическим алгоритмом (ПГА) позволяет повысить качество компоновки схем от 2% до 5%, в зависимости от задачи.
Системные требования: Pentium II 400, 128MB RAM, HDD 5MB.
Среда функционирования: MS Windows 9x, 2000, XP.

для цепей различной ширины позволяет получить топологию канальной области

с цепями, имеющими различную ширину. Алгоритм использует теорию эволюционного моделирования и методы генетического поиска.

Программный продукт канальной трассировки позволяет проводить экспериментальные исследования в автоматическом и пошаговом режиме.
Критерии оптимизации алгоритма канального трассировщика: ширина канальной области, суммарная длина цепей, число межслойных переходов.
Входные данные: число выводов; ширины цепей; номера цепей, подключаемых к выводам.
Выходные данные: топология канала
Среда функционирования: MS WINDOWS 98, XP 2000.
Системные требования: Pentium 333, 128Mb RAM, + 70 Mb дискового пространства, разреш. 800*600.

решает задачу размещения множества элементов в непересекающемся множестве позиций.

Используется новый критерий, учитывающий распределение ресурсов коммутационного поля. Процесс решения задачи размещения осуществляется адаптивной поисковой процедурой, основанной на сочетании генетического поиска с адаптацией на основе самообучения и самоорганизации

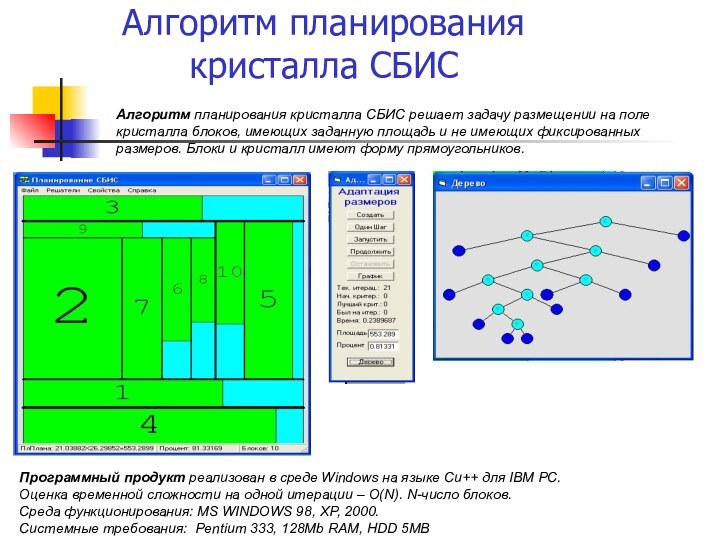
Программный продукт реализован в среде Windows на языке Си++ для IВМ РС
Временная сложность при совместной работе алгоритмов и при фиксированных значениях управляющих параметров на одной итерации имеет оценку О(n).
При совместной работе алгоритмов вероятность получения глобального оптимума составила 0.95. В среднем, трех запусков программы со случайными начальными популяциями достаточно для нахождения решения со средним отклонением от глобального оптимума в 1%.
Системные требования: Pentium II 400, 128MB RAM, HDD 5MB.
Среда функционирования: MS Windows 98, 2000, XP.

размещении на поле кристалла блоков, имеющих заданную площадь и

не имеющих фиксированных размеров. Блоки и кристалл имеют форму прямоугольников.

Программный продукт реализован в среде Windows на языке Си++ для IВМ РС.
Оценка временной сложности на одной итерации – О(N). N-число блоков.
Среда функционирования: MS WINDOWS 98, XP, 2000.
Системные требования: Pentium 333, 128Mb RAM, HDD 5MB