Презентация на тему Линия. Понятия и определения

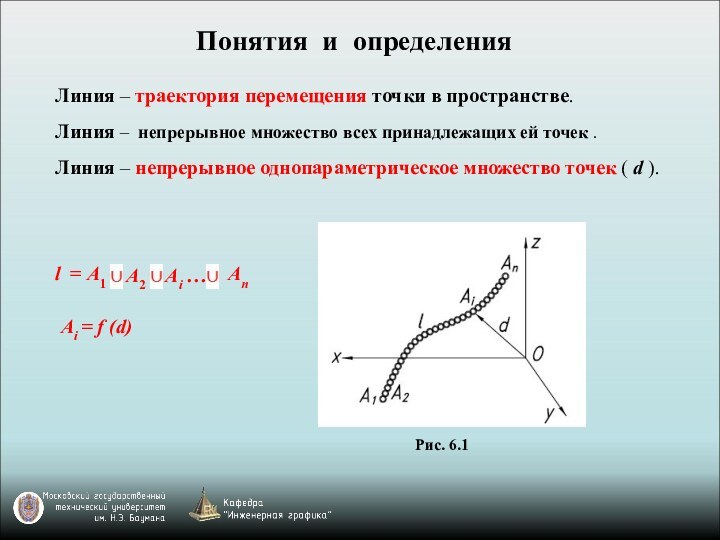
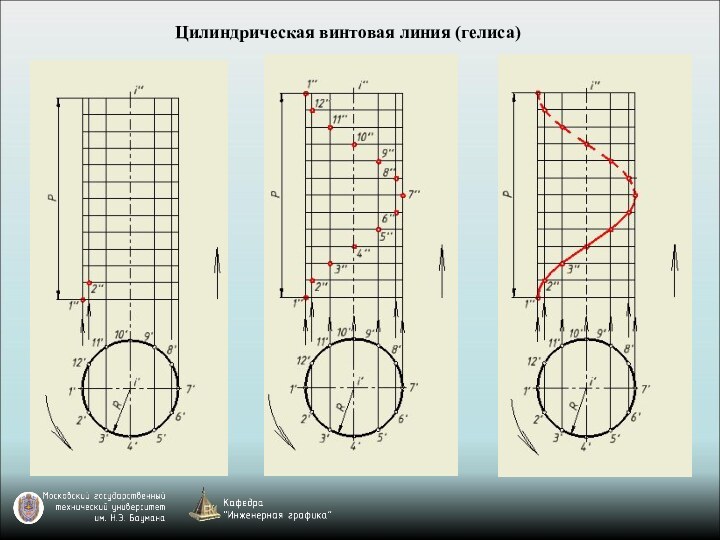
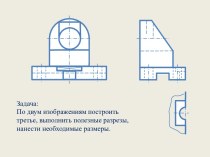
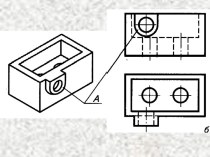
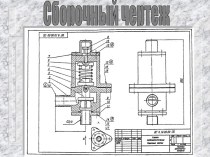
пространстве.
Линия – непрерывное множество всех принадлежащих ей точек .
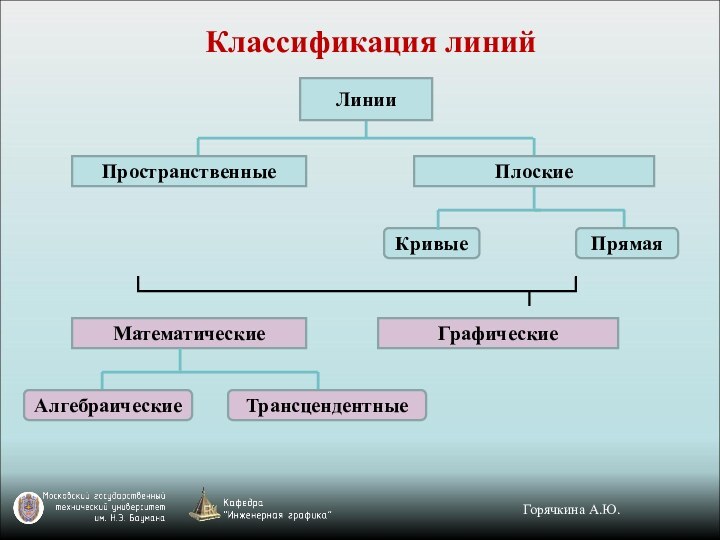
Линия

– непрерывное однопараметрическое множество точек ( d ).

Рис. 6.1

l = A1

A2

Ai …

An

Ai = f (d)

может быть выражена уравнением в какой-либо системе координат, то

такая кривая называется закономерной, например эллипс, парабола, гипербола и др.

Незакономерной называется кривая линия, в которой нельзя обнаружить закономерности образования, например линия пересечения рельефа местности плоскостью

прямоугольных координатах в виде многочлена n – степени, или

числом точек ее пересечения с компланарной ей прямой (для плоской линии (рис. 6.2),
числом точек ее пересечения с плоскостью (для пространственной линии (рис. 6.3).

Плоская линия (рис. 6.2) – линия, все точки которой принадлежат одной плоскости.
Пространственная линия (рис. 6.3) – линия, которая не может быть совмещена с плоскостью всеми своими точками.

Рис. 6.3

Рис. 6.2

проходит на другую сторону касательной прямой, сохраняя касание
Двойная или

узловая точка (B) – это точка, в которой кривая пересекает сама себя

Точки возврата первого рода (C) – это точка, в которой кривая подходит к точке двумя ветвями, имеющими в точке C общую касательную и расположенными по разные стороны от касательной

Точки возврата второго рода (D) – это точка, в которой кривая подходит к точке двумя ветвями, имеющими в точке D общую касательную, расположенную по одну сторону от обеих ветвей кривой

Особые точки плоской кривой

проецируется в касательную к ее проекции

2. Несобственной точке

линии соответствует несобственная точка ее проекции

3. Порядок проекции линии ( для алгебраических линий) равен порядку
самой лини

Число узловых точек равно числу точек самопересечения

Рис. 6.4

необходимая и достаточная
для однозначного построения проекции любой точки линии.
Построение

проекции любой точки линии позволяет решить вопрос о характере
линии (плоская или пространственная).

Способ хорд

Рис. 6.5

ТЕОРЕМА. Если точка принадлежит линии, то проекции точки принадлежат
одноименным проекциям линии: A l <=> A' l ' ᴧ A'' l ''

Принадлежность точки линии

пересекающая кривую линию в одной, двух и более точках,

называется секущей (AB).

Предельное положение секущей, которое занимает последняя при сближении точек А и В секущей АВ до слияния их в одну точку, называется полукасательной к кривой l в точке A.
Две полукасательные образуют касательную t к кривой в данной точке А.

Нормалью n к плоской кривой в точке А называется прямая, перпендикулярная к касательной t в этой точке (рис. 6.6).

Рис. 6.6

n ┴ t

одну нормаль.

Касательные и нормали плоской кривой всегда лежат в

плоскости этой кривой) ( рис. 6.7, 6.8)

Рис. 6.8

Рис. 6.7

6.9) считается предел, к которому стремится отношение угла между

касательными, проведенными в соседних точках A1 и A2 кривой, к дуге A1A2, если точка A2 стремится к точке A1.

Рис. 6.9

Кривизна плоской кривой

Круг кривизны (рис. 6.10) – окружность, проходящая через точку A и имеющая с данной кривой в этой точке общую касательную и одинаковое направление выпуклости.
Радиус круга кривизны – радиус кривизны (r) кривой в данной точке, а центр круга кривизны – центр кривизны кривой в данной точке.

Рис. 6.10

двух движений – вращательного вокруг некоторой оси и
поступательного

относительно этой же оси;
смещение при поступательном движении пропорционально углу поворота.

Шаг винтовой линии (P) – смещение точки вдоль оси за один оборот.

По направлению движения различают правую и левую винтовые линии.

Винтовая линия называется цилиндрической, если поступательное движение
осуществляется по образующей воображаемого цилиндра;
конической – при движении вдоль образующей воображаемого конуса.

Пространственные кривые. Винтовая линия