Презентация на тему Многогранники и их виды. Графические модели многогранников. (Лекция 5)

Многогранником называется пространственная фигура,
ограниченная замкнутой поверхностью, состоящей

из от-
секов плоскостей, имеющих форму многоугольников.
Стороны многоугольников образуют рёбра, а плоскости многоугольников - грани многогранника. Если вершины
и ребра многогранника находятся по одну сторону плос-
кости любой из его граней, то многогранник называют выпуклым, все его грани – выпуклые.
Из всего многообразия многогранников наибольший
практический интерес представляют призмы, пирами-
ды, правильные многогранники и их разновидности.
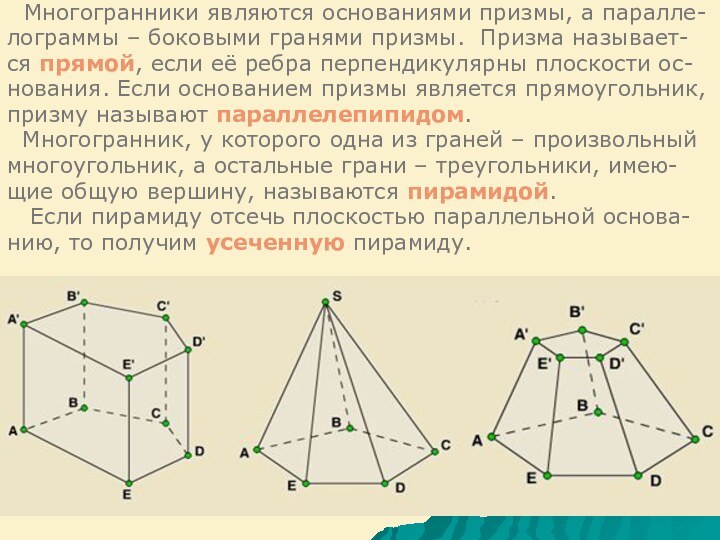
Многогранник, две грани которого n-угольники в
параллельных плоскостях, а остальные n-граней –
параллелограммы, называется n-угольной призмой.

Многогранники являются основаниями призмы, а

паралле-
лограммы – боковыми гранями призмы. Призма называет-
ся прямой, если её ребра перпендикулярны плоскости ос-
нования. Если основанием призмы является прямоугольник,
призму называют параллелепипидом.
Многогранник, у которого одна из граней – произвольный
многоугольник, а остальные грани – треугольники, имею-
щие общую вершину, называются пирамидой.
Если пирамиду отсечь плоскостью параллельной основа-
нию, то получим усеченную пирамиду.

грани являются правильными многоугольниками. К
ним относятся куб, тетраэдр,

октаэдр, икосаэдр, додекаэдр.
Такие выпуклые правильные многогранники называют тела
Платона.

В каждой вершине правильного многогранника сходится
одно и то же число рёбер. Все двугранные углы при рёбрах и все многогранные углы при вершинах  правильного мно- гоугольника равны.
Правильные многогранники - трехмерный аналог плоских
правильных многоугольников. 

многогранников существу-ют аналоги платоновых тел - четыре правильных невы-

пуклых однородных многогранника или тела Кеплера-
Пуансо.
Все грани таких многогранников - одинаковые правильные многоугольники, и все многогранные углы которых равны. Грани при этом могут быть как выпуклыми, так и невыпук-
лыми.

выпуклые многогранники, то есть выпуклые многогранники, все многогранные углы

которых равны, а грани - правильные многоугольники нескольких типов.

изображению ре-
бер – линий пересечения граней и вершины –

точек пересе-
чения ребер.

Наличие на чертеже только прямолинейных отрезков, ко- торые являются проекциями
ребер или граней, служит при- признаком, позволяющим уста- новить, что на чертеже изобра- жен многогранник.
Графически простую много- гранную поверхность удобно задавать проекциями ее сетки.
Многогранник АВСD задан проекциями его ребер и вер- шин (сетки).

проекции K1 точки K по заданной ее фронтальной проекции

K2 из условия принадлежности точки K грани BB'C'C. Горизонтальная проекция точки K построена с помощью вспомогательной прямой 23, проведенной через точку K в плоскости BB'C'C.
Чертеж многогранной поверхности АВСDА'В'С'D', когда можно построить проекцию любой точки, принадлежащей многогранной поверхности называется полным.

результате пересече-
ния многогранника плоскостью, называется сечением многогран-ника.
Сечение

представляет собой плоский многоугольник с внутрен-
ней областью. В частном случае эти многоугольники могут распа-
даться на несколько многогранников, вырождаться в прямые и точ-
ки.
Сечение многогранника плоскостью можно построить двумя способами:
1. По точкам пересечения с плоскостью ребер многогранника.
2. По линиям пересечения граней многогранника с плоскостью.
В первом случае задача сводится к определению точек пересече-
ния прямой с плоскостью.
Во втором случае - к определению линий пересечения плоскостей.
В ряде случаев целесообразно комбинированное применение обо-
их способов.