А С Ч Е Т А
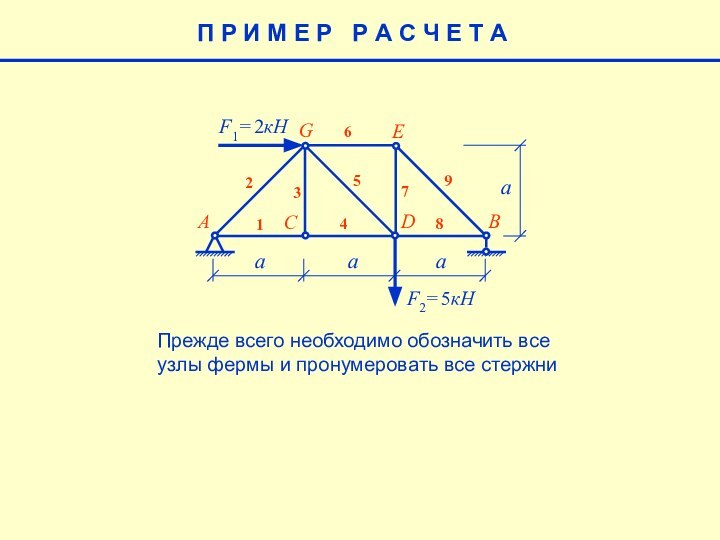
Прежде всего необходимо обозначить
всеузлы фермы и пронумеровать все стержни
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Определить усилия во всех стержнях фермы методом вырезания узлов
Содержание
- 2. ABCDEG123456789П Р И М Е Р
- 3. П Р И М Е Р
- 4. П Р И М Е Р
- 5. aF1= 2кНF2= 5кНABCDEG123456789XA+F1= 0XA = – F1
- 6. aF1= 2кНF2= 5кНABCDEG123456789(-2)(4)(1)П Р И М Е Р Р А С Ч Е Т А
- 7. Проверка: Для проверки правильности полученных
- 8. EaF1= 2кНF2= 5кНABCDG123456789(-2)(4)(1)XA∙a – YA ∙2a +
- 9. П Р И М Е Р Р А С Ч Е Т А
- 10. МЕТОД ВЫРЕЗАНИЯ УЗЛОВП Р
- 11. Поэтому равновесие узлов нужно рассматривать
- 12. Поэтому равновесие узлов нужно рассматривать
- 13. П Р И М Е Р
- 14. EaF1= 2кНF2= 5кНABCDG123456789(-2)(4)(1)Правило знаков:«+» – растягивающие усилия
- 15. EaF1= 2кНF2= 5кНABCDG123456789(-2)(4)(1)Узел В:yYB = 4x– S8
- 16. YB sin 450– S9 cos 450
- 17. √ 2 2EaF1= 2кНF2= 5кНABCDG123456789(-2)(4)(1)Узел В:YB =
- 18. Узел Е:EaF1= 2кНF2= 5кНABCDG123456789(-2)(4)(1)Узел В:y4 П Р
- 19. = – 4 (кН);Узел Е:4 x– S6
- 20. П Р И М Е Р
- 21. 4 – 44(4)Узел D :S7 = 4xS8
- 22. 4 – 44(4)√2 3П Р И М
- 23. 4 – 44(4)3Узел С : 30 30П
- 24. Узел А:4 – 44(4)3 30П Р И
- 25. 4 – 44(4)3 30Узел А:П Р И
- 26. 4 – 44(4)3 30Узел А:ПроверкаУзел А: XA
- 27. 4 – 443 30ПроверкаУзел А:П Р И
- 28. Скачать презентацию
- 29. Похожие презентации
ABCDEG123456789П Р И М Е Р Р А С Ч Е Т АПрежде всего необходимо обозначить всеузлы фермы и пронумеровать все стержни
Слайд 3 П Р И М Е Р Р
А С Ч Е Т А
Полный расчёт
фермы, при котором необходимо определить усилия во всех стержнях, имеет смысл начать с определения реакций опор. Для этого рассматривается равновесие всей фермы.Слайд 4 П Р И М Е Р Р
А С Ч Е Т А
Выбор формы
условий равновесия зависит от количества и расположения опор. Нужно составлять уравнения таким образом, чтобы из каждого уравнения определялась одна составляющая реакций опор.ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ОПОР ФЕРМЫ
Слайд 5
a
F1= 2кН
F2= 5кН
A
B
C
D
E
G
1
2
3
4
5
6
7
8
9
XA+F1= 0
XA = – F1 =
– 2 (кН)
(-2)
– 2
YA – F2 + YB= 0
–
F1∙a – F2 ∙2a + YB ∙3a = 0(4)
4
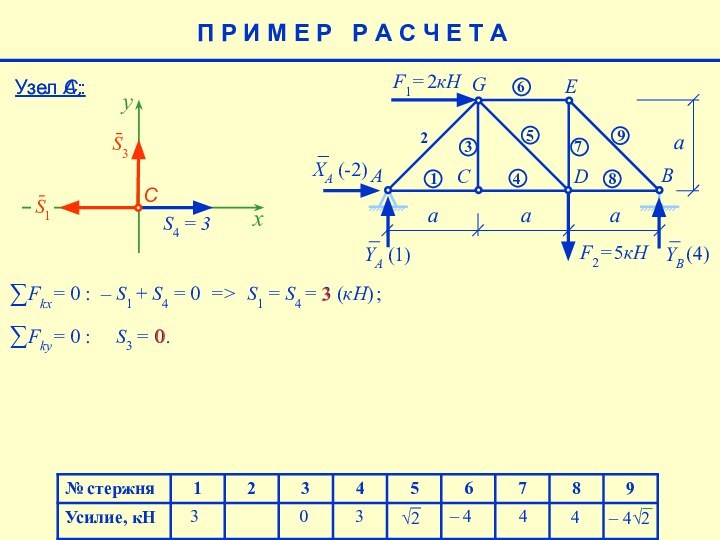
YA = F2 – YB = 5 – 4= 1(кН)
1
(1)
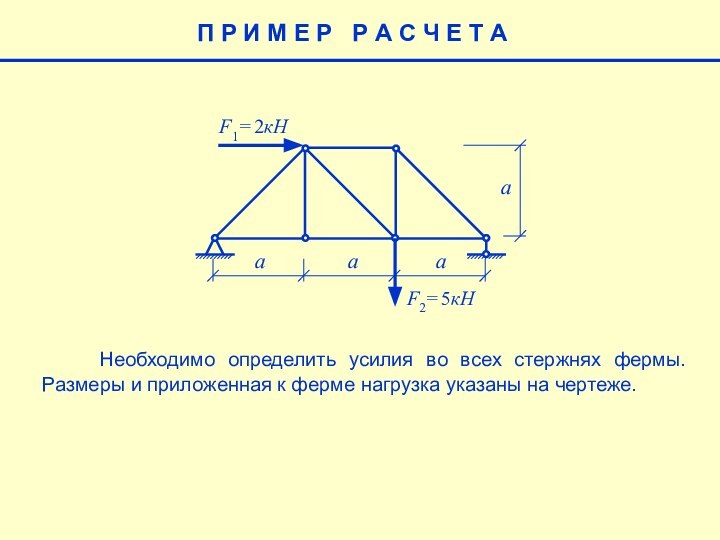
П Р И М Е Р Р А С Ч Е Т А
Слайд 7
Проверка:
Для проверки правильности полученных результатов
составим уравнение моментов относительно такой точки,
относительно которой все
вычисленные силы реакций создают ненулевые моменты.
a
F1= 2кН
F2= 5кН
A
B
C
D
E
G
1
2
3
4
5
6
7
8
9
(-2)
(4)
(1)
П Р И М Е Р Р А С Ч Е Т А
Слайд 8
E
a
F1= 2кН
F2= 5кН
A
B
C
D
G
1
2
3
4
5
6
7
8
9
(-2)
(4)
(1)
XA∙a – YA ∙2a + YB
∙a
= –2 ∙a – 1 ∙2a + 4 ∙a
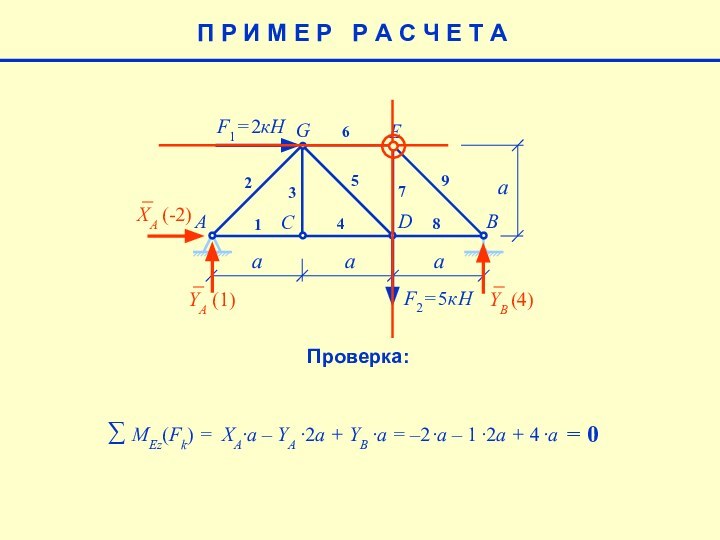
= 0
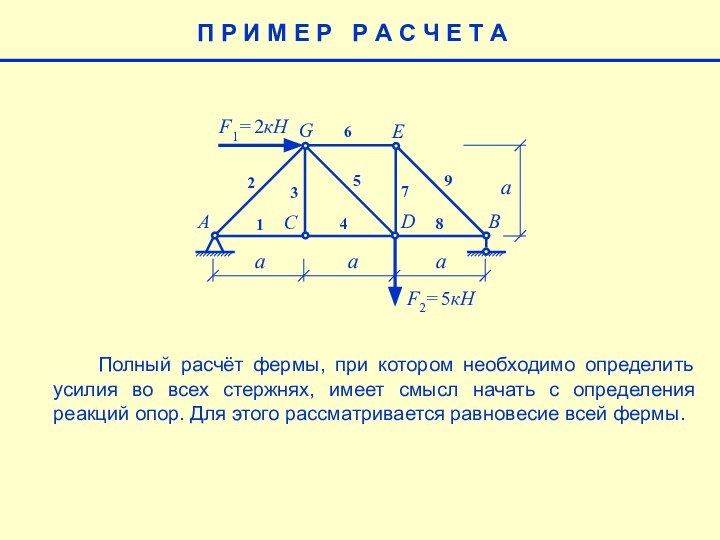
П Р И М Е Р Р А С Ч Е Т А
Проверка:
Слайд 10
МЕТОД ВЫРЕЗАНИЯ УЗЛОВ
П Р И
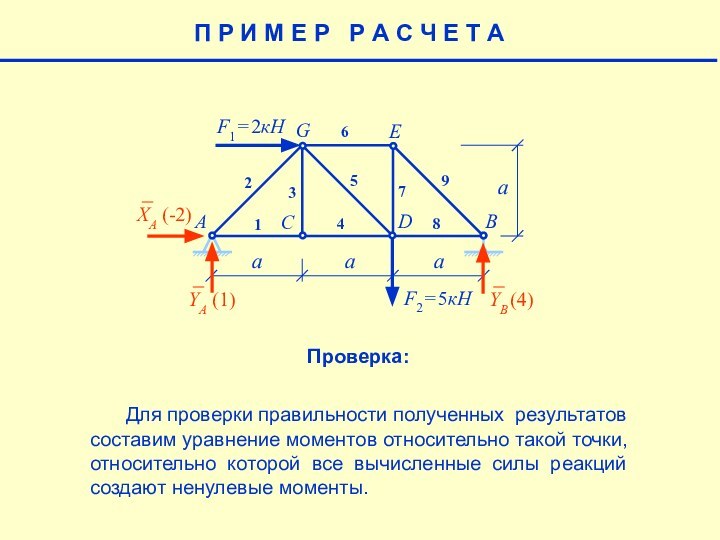
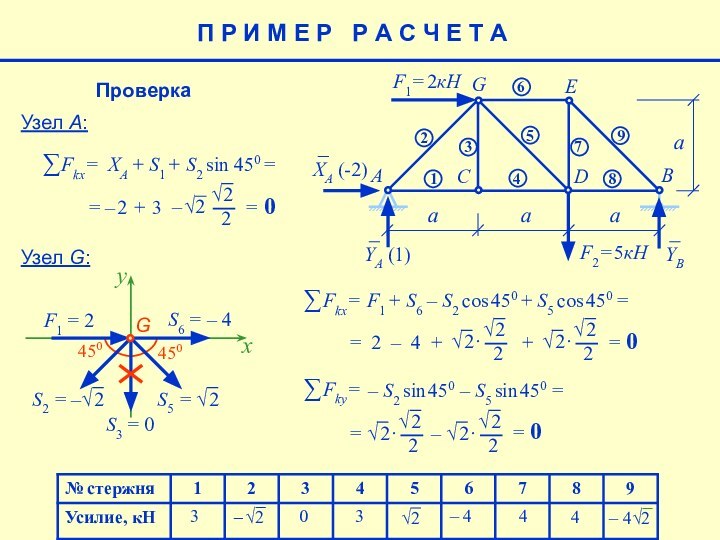
М Е Р Р А С Ч Е
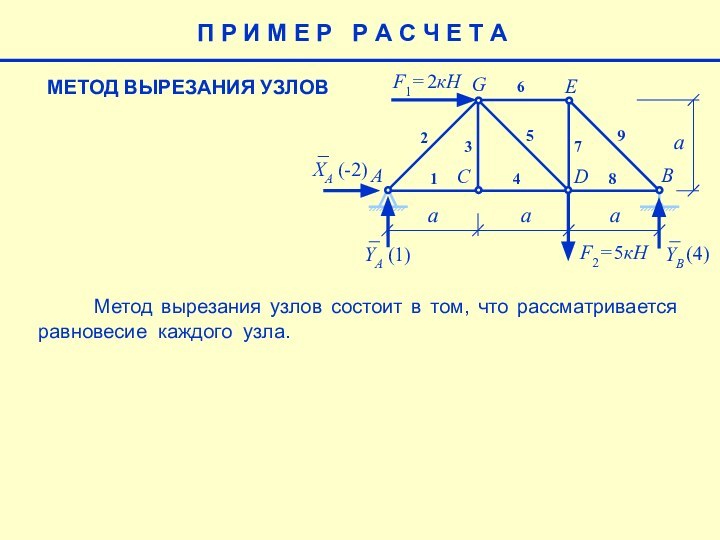
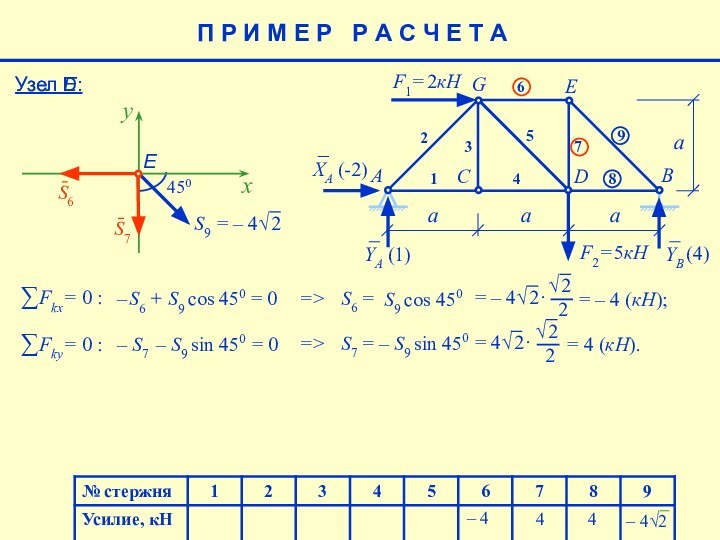
Т А Метод вырезания узлов состоит в том, что рассматривается равновесие каждого узла.
Слайд 11 Поэтому равновесие узлов нужно рассматривать в
определённой последовательности, позволяющей на каждом шаге решения задачи определять
две очередные неизвестные.E
a
F1= 2кН
F2= 5кН
A
B
C
D
G
1
2
3
4
5
6
7
8
9
(-2)
(4)
(1)
П Р И М Е Р Р А С Ч Е Т А
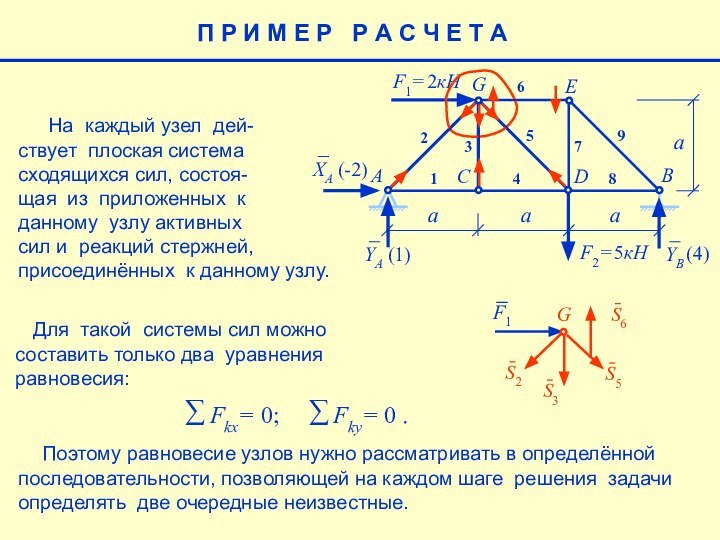
На каждый узел дей-
ствует плоская система
сходящихся сил, состоя-
щая из приложенных к
данному узлу активных
сил и реакций стержней,
присоединённых к данному узлу.
Для такой системы сил можно составить только два уравнения равновесия:
Слайд 12 Поэтому равновесие узлов нужно рассматривать в
определённой последовательности, позволяющей на каждом шаге решения задачи определять
две очередные неизвестные.П Р И М Е Р Р А С Ч Е Т А
На каждый узел дей-
ствует плоская система
сходящихся сил, состоя-
щая из приложенных к
данному узлу активных
сил и реакций стержней,
присоединённых к данному узлу.
Для такой системы сил можно составить только два уравнения равновесия:
E
a
F1= 2кН
F2= 5кН
A
B
C
D
G
1
2
3
4
5
6
7
8
9
(-2)
(4)
(1)
Слайд 13 П Р И М Е Р Р
А С Ч Е Т А
На
каждый узел дей-ствует плоская система
сходящихся сил, состоя-
щая из приложенных к
данному узлу активных
сил и реакций стержней,
присоединённых к данному узлу.
Для такой системы сил можно составить только два уравнения равновесия:
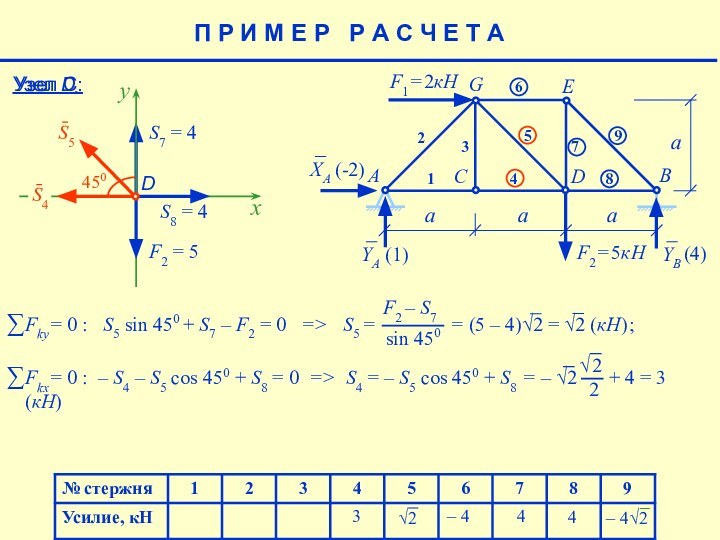
Поэтому равновесие узлов нужно рассматривать в определённой последовательности, позволяющей на каждом шаге решения задачи определять две очередные неизвестные.
E
a
F1= 2кН
F2= 5кН
A
B
C
D
G
1
2
3
4
5
6
7
8
9
(-2)
(4)
(1)
Слайд 14
E
a
F1= 2кН
F2= 5кН
A
B
C
D
G
1
2
3
4
5
6
7
8
9
(-2)
(4)
(1)
Правило знаков:
«+» – растягивающие усилия
(направлены
от узла);
«–» – сжимающие усилия.
П Р И М Е
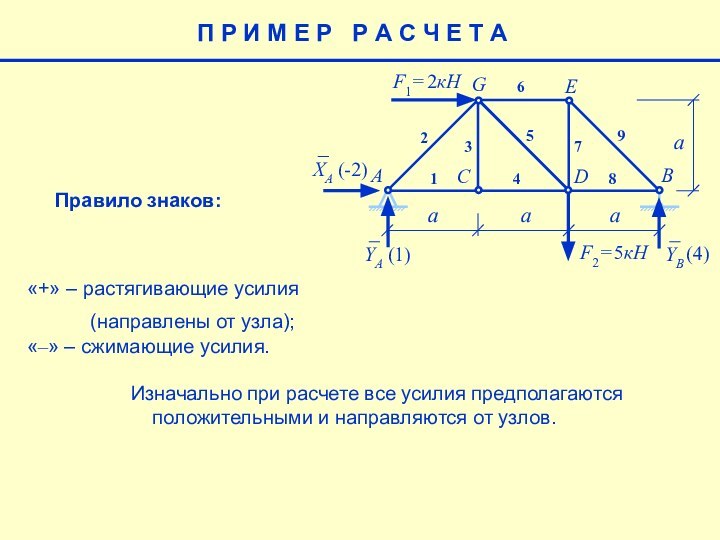
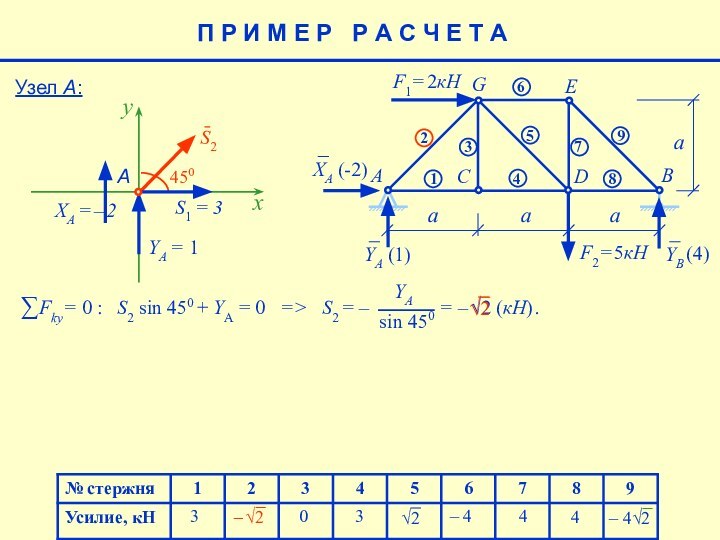
Р Р А С Ч Е Т А Изначально при расчете все усилия предполагаются положительными и направляются от узлов.
Слайд 15
E
a
F1= 2кН
F2= 5кН
A
B
C
D
G
1
2
3
4
5
6
7
8
9
(-2)
(4)
(1)
Узел В:
y
YB = 4
x
– S8
–
S9 cos 450
= 0 ;
YB
+ S9
sin 450 = 0 .
П Р И М Е Р Р А С Ч Е Т А
Слайд 16
YB
sin 450
– S9 cos 450
E
a
F1=
2кН
F2= 5кН
A
B
C
D
G
1
2
3
4
5
6
7
8
9
(-2)
(4)
(1)
Узел В:
YB = 4
x
y
– S8
– S9 cos
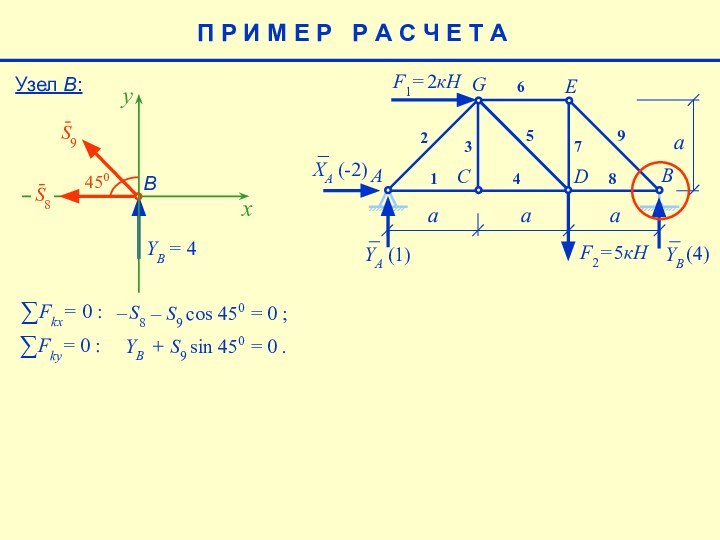
450 = 0 ;
YB
+ S9 sin 450
= 0 .
(2) => S9 =
=
4
(1) => S8 =
= 4 (кН).
П Р И М Е Р Р А С Ч Е Т А
Слайд 17
√ 2
2
E
a
F1= 2кН
F2= 5кН
A
B
C
D
G
1
2
3
4
5
6
7
8
9
(-2)
(4)
(1)
Узел В:
YB = 4
x
y
–
S8
– S9 cos 450
= 0 ;
YB
+ S9 sin 450
= 0 .
(2) => S9 =
YB
sin 450
=
4
(1) => S8 =
– S9 cos 450
= 4√ 2 ∙
= 4 (кН).
П Р И М Е Р Р А С Ч Е Т А
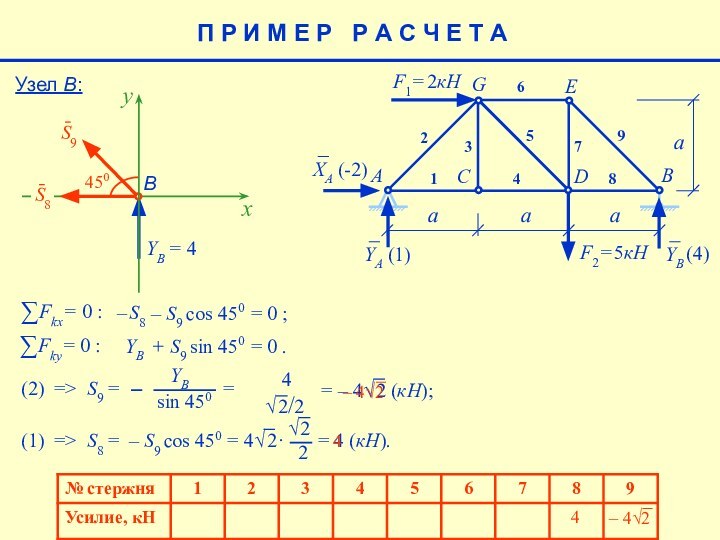
4
4
Слайд 19
= – 4 (кН);
Узел Е:
4
x
– S6
+
S9 cos 450
= 0
y
=> S6 =
S9
cos 450– S7
– S9 sin 450
= 0
=> S7 =
– S9 sin 450
= 4 (кН).
– 4
– 4
4
4
П Р И М Е Р Р А С Ч Е Т А
Слайд 26
4
– 4
4
(4)
3
3
0
Узел А:
Проверка
Узел А:
XA
+ S1
+ S2 sin 450 =
= – 2
+
3= 0
П Р И М Е Р Р А С Ч Е Т А
