- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Поверхности. Основные понятия и определения
Содержание
- 2. Свойства принадлежности точки и линии поверхности1.Точка принадлежит
- 3. Классификация поверхностей
- 4. Многогранные поверхности (пирамидальные,
- 5. Пирамидальные поверхностиОпределитель пирамидальной поверхности: Φ (m, S)
- 6. Чтобы задать поверхность на чертеже необходимо:1. Построить
- 7. 12Комплексный чертеж пирамидальной поверхности(m, S)l ∩ m, l ⊃ S
- 8. Призматические поверхности Определитель призматической поверхности:Δ (m, s)
- 9. Комплексный чертеж призматической поверхности12Δ (m, s) l ∩ m, l // s
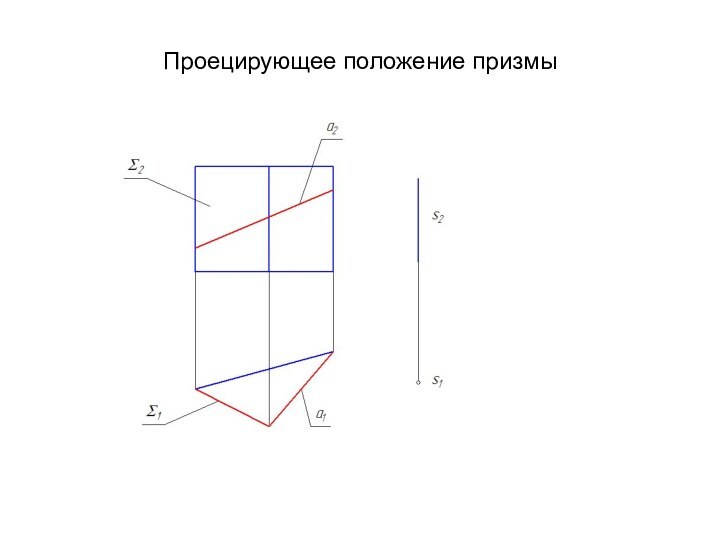
- 10. Проецирующее положение призмы
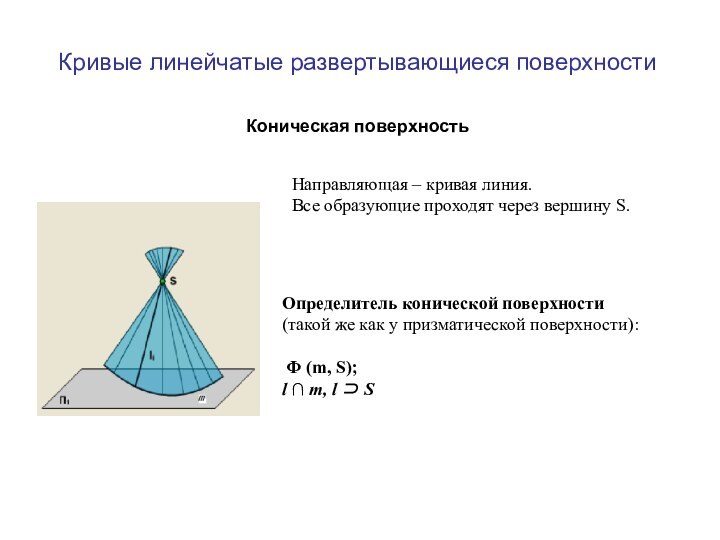
- 11. Кривые линейчатые развертывающиеся поверхности Коническая поверхностьОпределитель
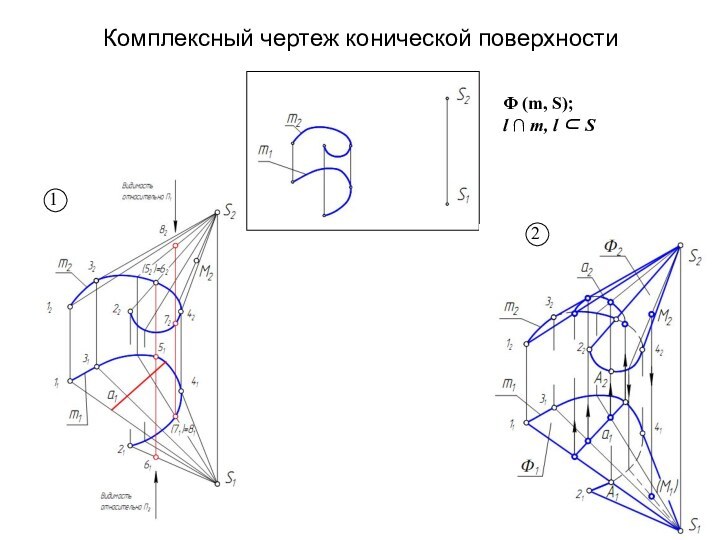
- 12. Комплексный чертеж конической поверхности21Φ (m, S);l ∩ m, l ⊂ S
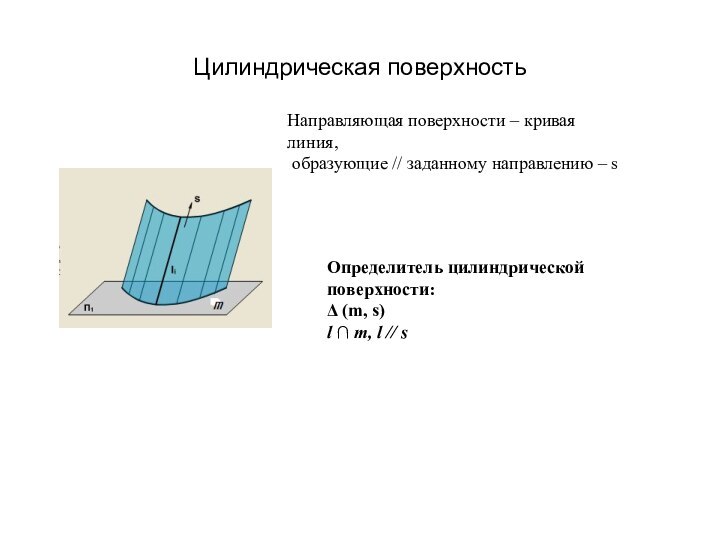
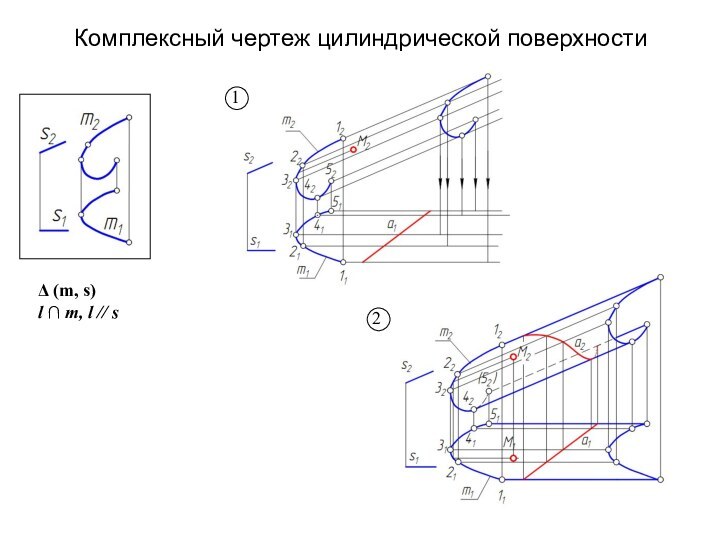
- 13. Цилиндрическая поверхностьОпределитель цилиндрической поверхности:Δ (m, s) l
- 14. Комплексный чертеж цилиндрической поверхности12Δ (m, s) l ∩ m, l // s
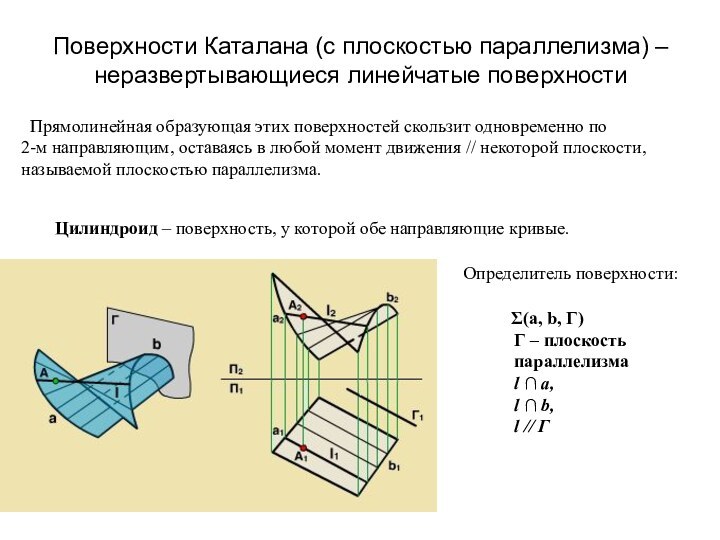
- 15. Поверхности Каталана (с плоскостью параллелизма) – неразвертывающиеся
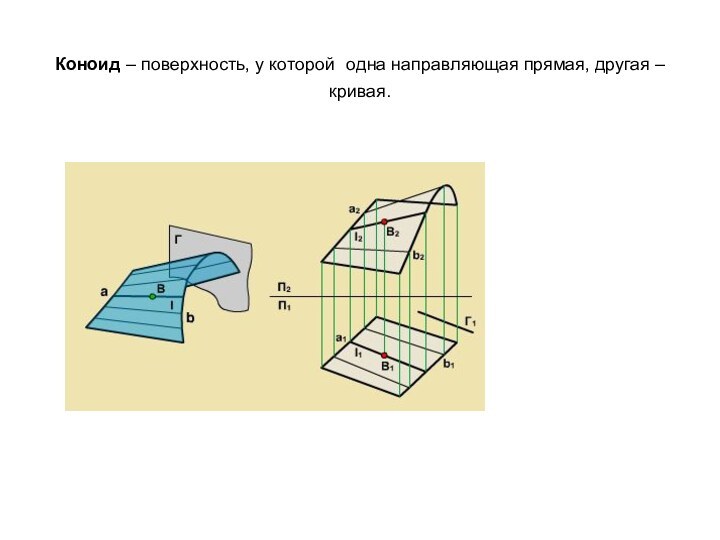
- 16. Коноид – поверхность, у которой одна направляющая прямая, другая – кривая.
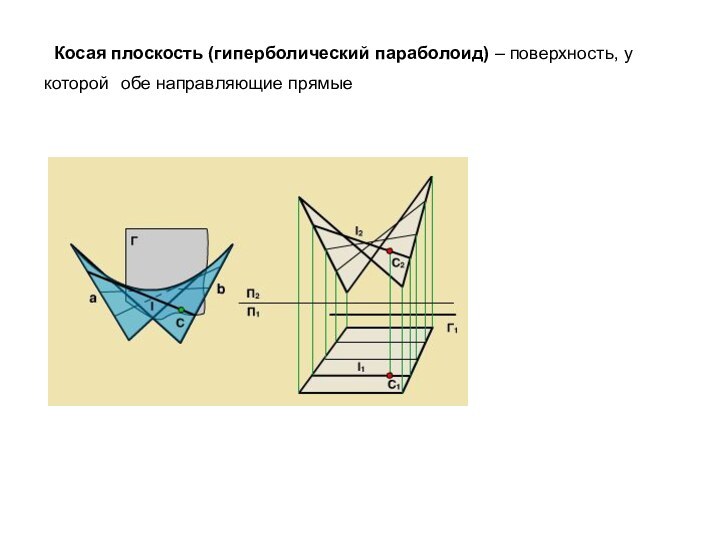
- 17. Косая плоскость (гиперболический параболоид) – поверхность, у которой обе направляющие прямые
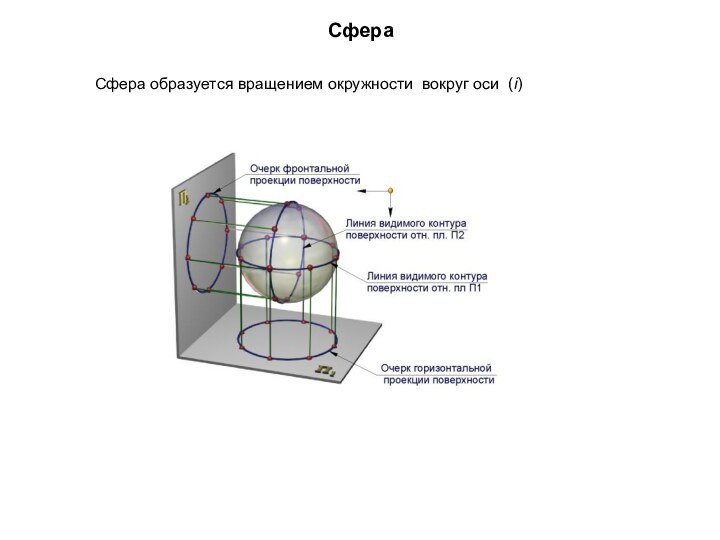
- 18. Поверхности вращения Эти поверхности описываются какой-либо
- 19. - определитель поверхности
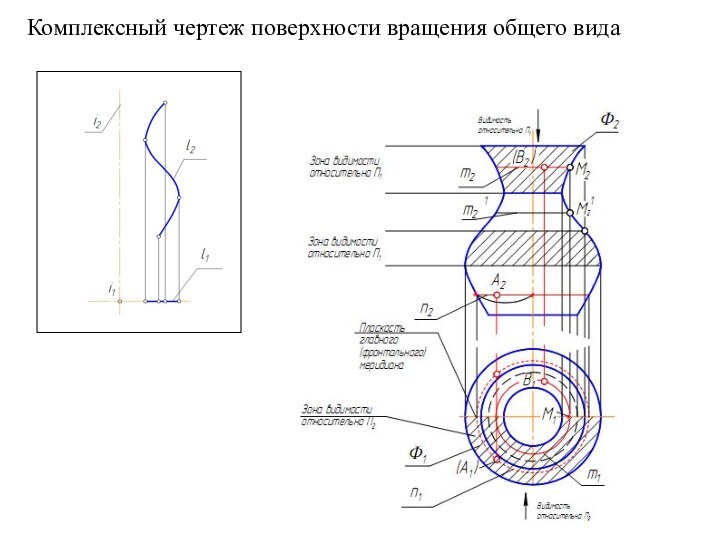
- 20. Комплексный чертеж поверхности вращения общего вида
- 21. Поверхности вращения 2-го порядка. Цилиндр вращения –проецирующая поверхность. Комплексный чертеж
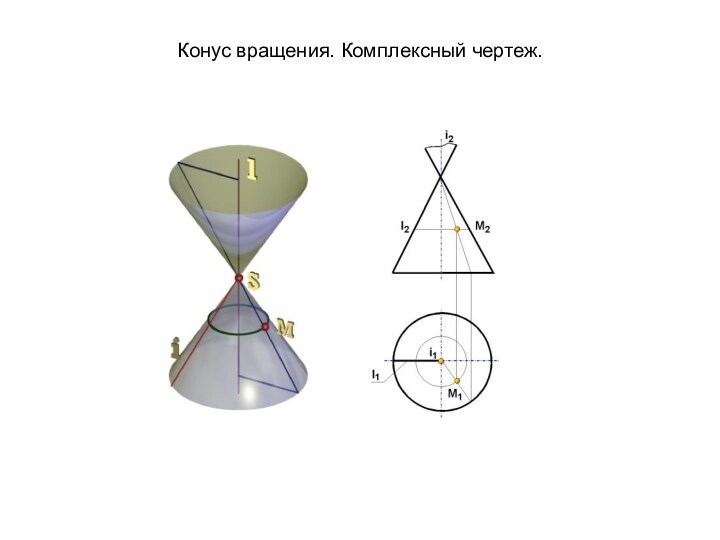
- 22. Конус вращения. Комплексный чертеж.
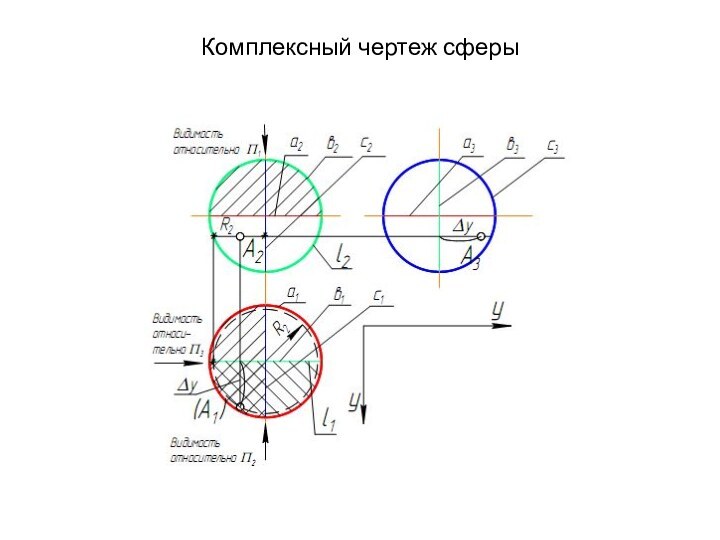
- 24. Комплексный чертеж сферы
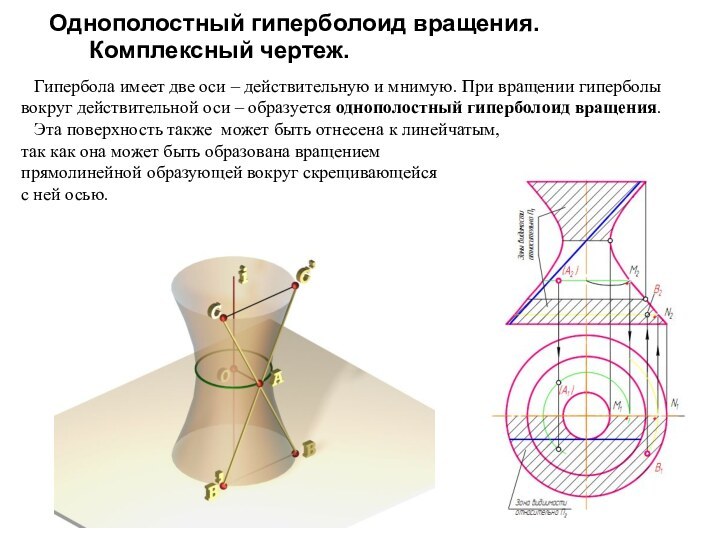
- 25. Однополостный гиперболоид вращения. Комплексный чертеж.
- 26. При вращении гиперболы вокруг мнимой оси – образуется две полости гиперболоида или двуполостный гиперболоид вращения.
- 27. Эллипсоид вращения При вращении
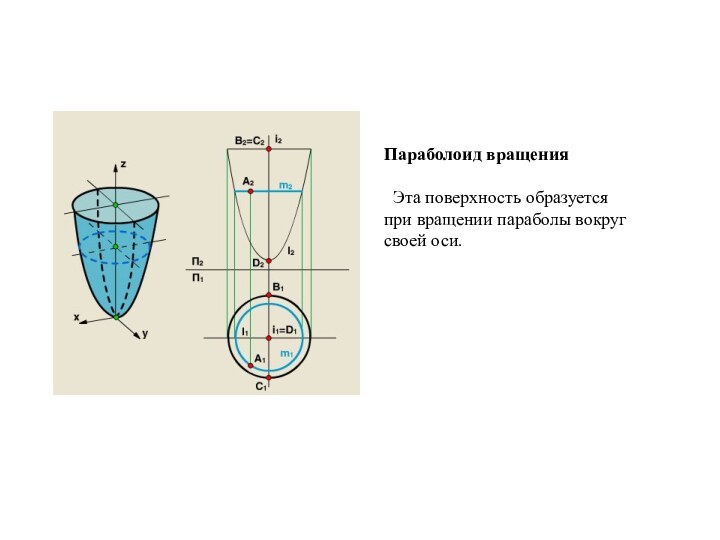
- 28. Параболоид вращения Эта поверхность образуется при вращении параболы вокруг своей оси.
- 29. Тор - поверхность вращения 4-го порядкаЕсли R
- 30. Если R > либо = r, то
- 31. При вращении дуги окружности, образуется поверхность тора, которая называется глобоид.
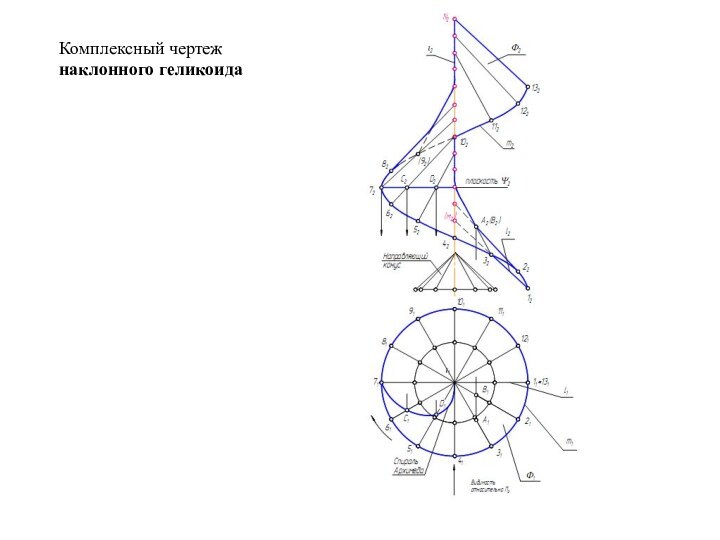
- 33. Комплексный чертежнаклонного геликоида
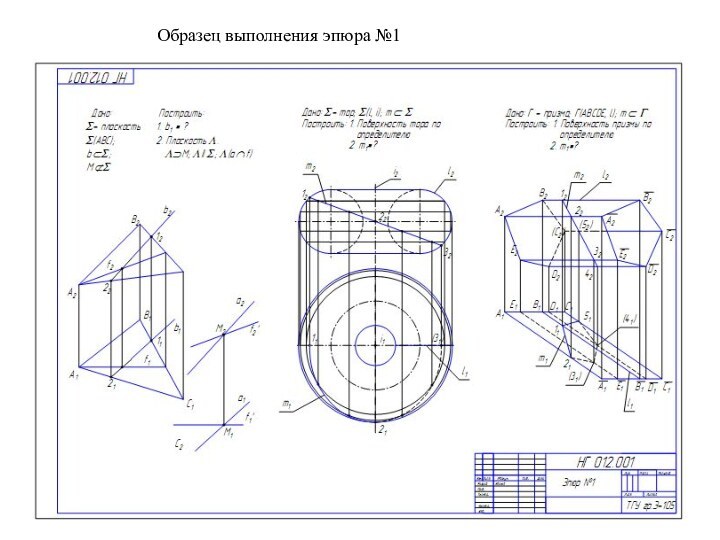
- 34. Образец выполнения эпюра №1
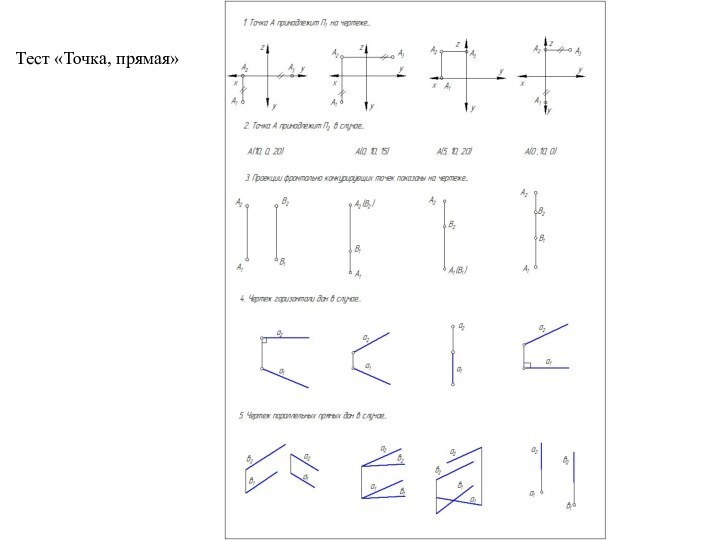
- 35. Тест «Точка, прямая»
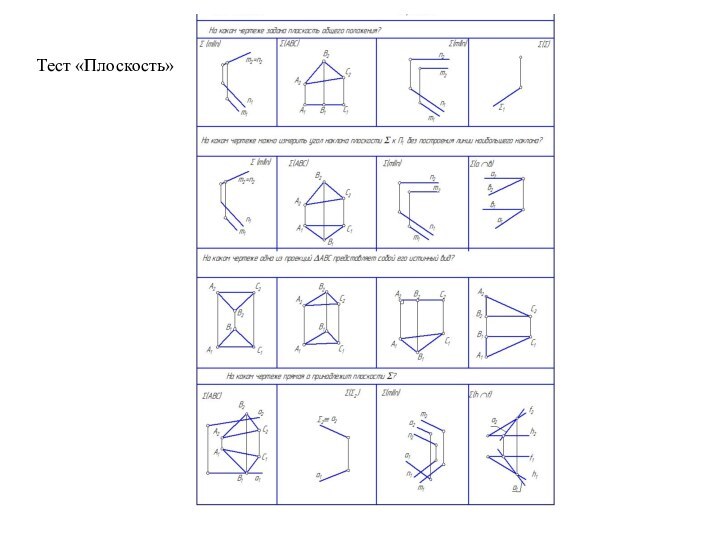
- 36. Тест «Плоскость»
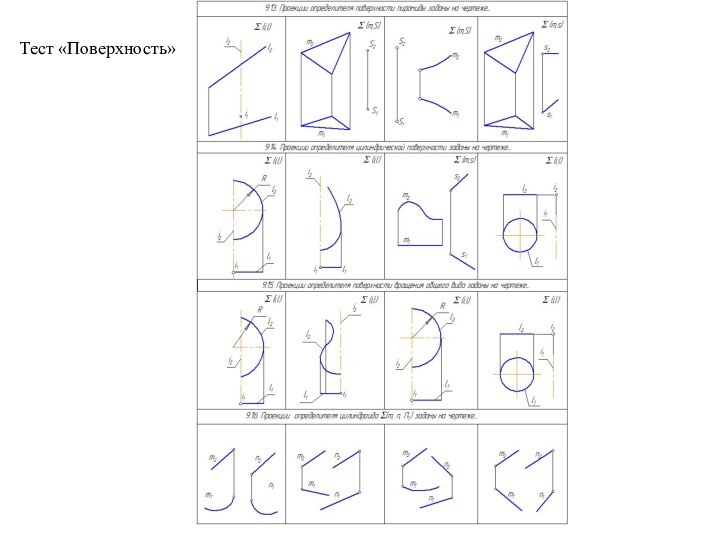
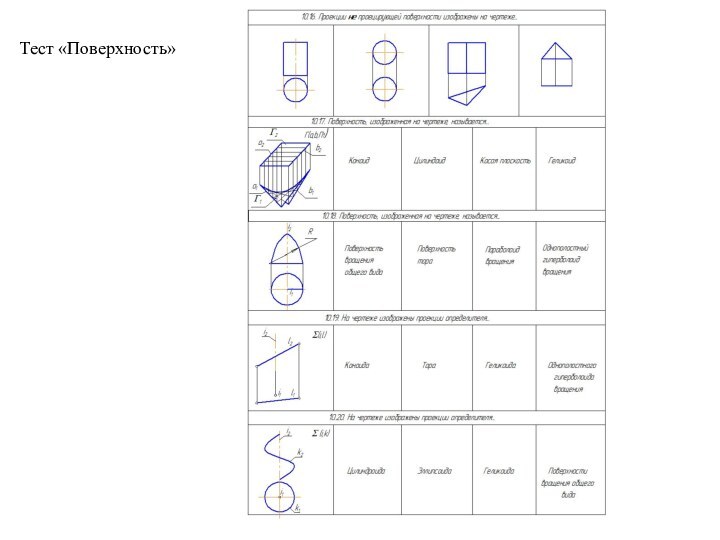
- 37. Тест «Поверхность»
- 38. Скачать презентацию
- 39. Похожие презентации
Свойства принадлежности точки и линии поверхности1.Точка принадлежит поверхности, если она принадлежит линии, лежащей на поверхности.2.Линия принадлежит поверхности, если все ее точки принадлежат поверхности.



Слайд 2
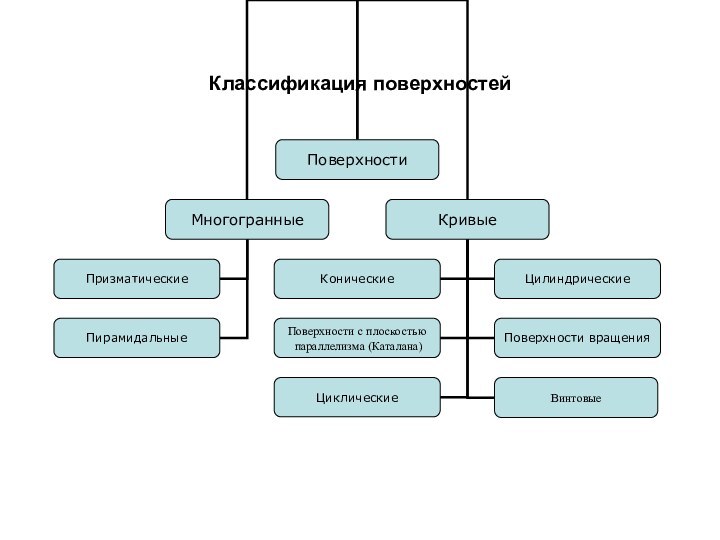
Свойства принадлежности точки и линии поверхности
1.Точка принадлежит поверхности,
если она принадлежит линии,
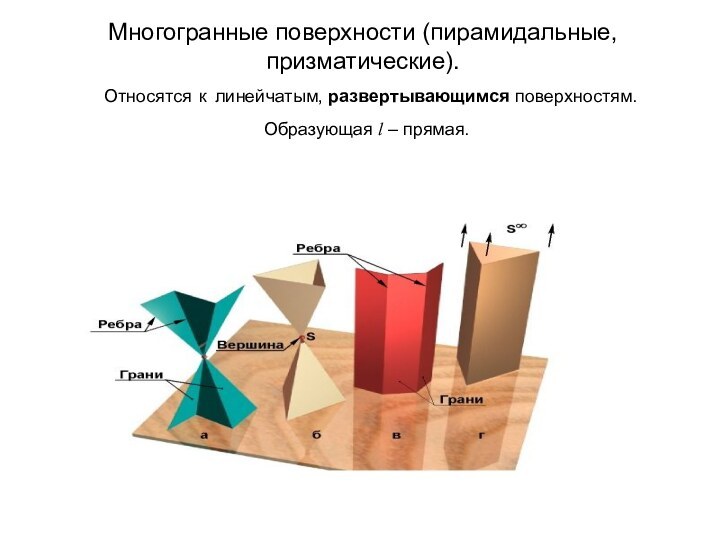
если все ее точки принадлежат поверхности.Слайд 4 Многогранные поверхности (пирамидальные, призматические). Относятся
к линейчатым, развертывающимся поверхностям.
Образующая l – прямая.
Слайд 5
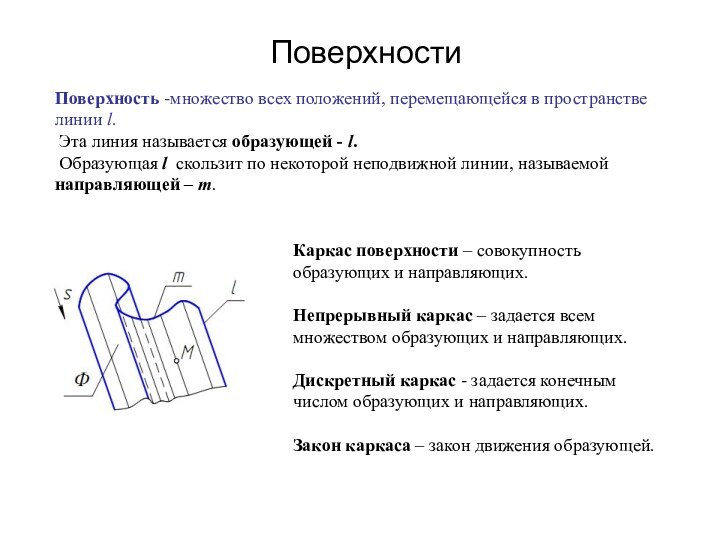
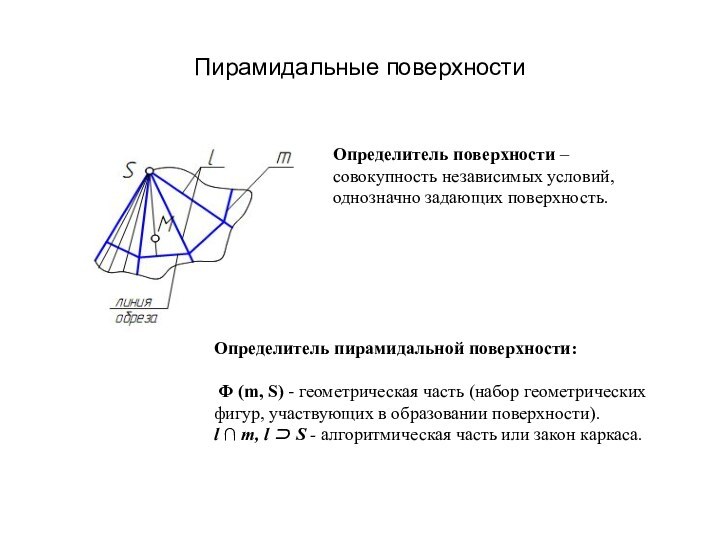
Пирамидальные поверхности
Определитель пирамидальной поверхности:
Φ (m, S) -
геометрическая часть (набор геометрических фигур, участвующих в образовании поверхности).
l
∩ m, l ⊃ S - алгоритмическая часть или закон каркаса.Определитель поверхности – совокупность независимых условий, однозначно задающих поверхность.
Слайд 6
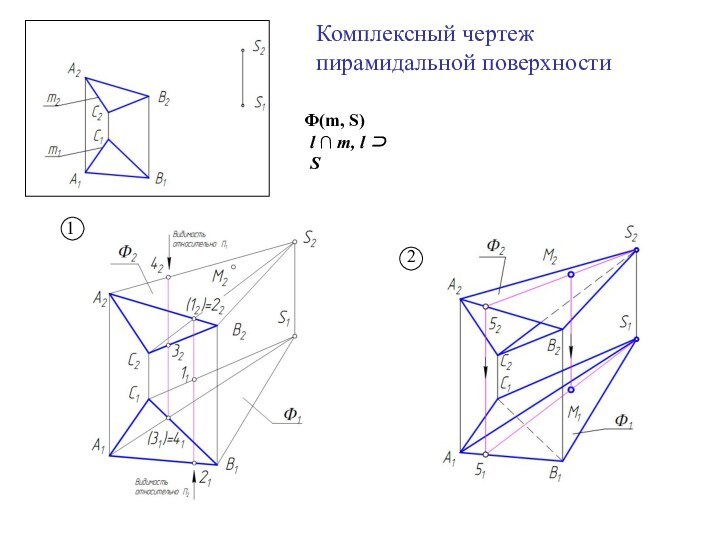
Чтобы задать поверхность на чертеже необходимо:
1. Построить проекции
определителя.
2. Построить проекции очерковых образующих поверхности и линии обреза.
3.
Определить видимость очерковых образующих.
Слайд 8
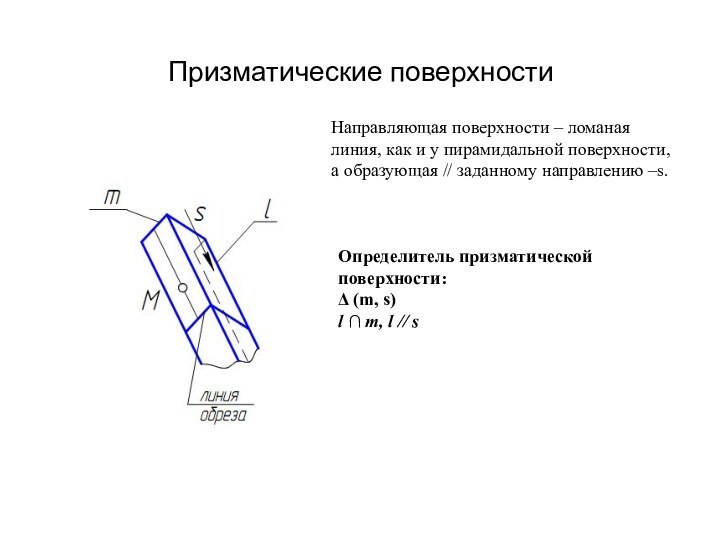
Призматические поверхности
Определитель призматической поверхности:
Δ (m, s)
l
∩ m, l // s
Направляющая поверхности – ломаная
линия, как
и у пирамидальной поверхности,а образующая // заданному направлению –s.
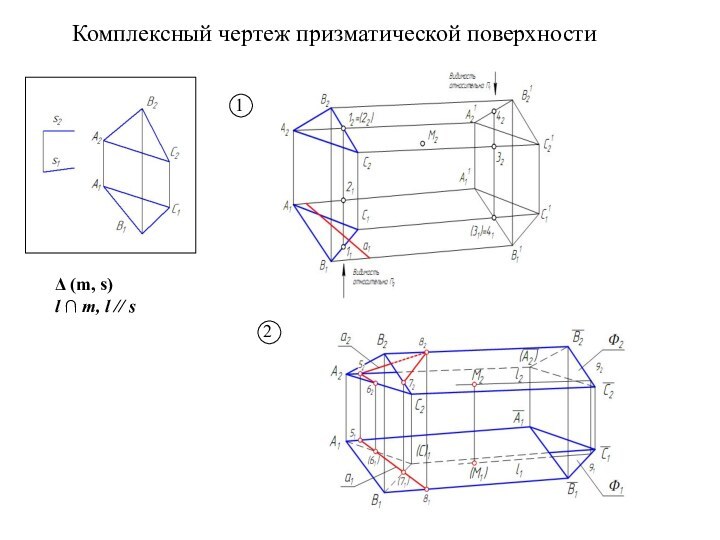
Слайд 11
Кривые линейчатые развертывающиеся поверхности
Коническая поверхность
Определитель конической поверхности
(такой же
как у призматической поверхности):
Φ (m, S);
l ∩ m,
l ⊃ S Направляющая – кривая линия.
Все образующие проходят через вершину S.
Слайд 13
Цилиндрическая поверхность
Определитель цилиндрической поверхности:
Δ (m, s)
l ∩
m, l // s
Направляющая поверхности – кривая
линия,
образующие //
заданному направлению – sСлайд 15 Поверхности Каталана (с плоскостью параллелизма) – неразвертывающиеся линейчатые
поверхности
Цилиндроид – поверхность, у которой обе направляющие кривые.
(а, b,
Г)Г – плоскость параллелизма
l ∩ a,
l ∩ b,
l // Г
Определитель поверхности:
Прямолинейная образующая этих поверхностей скользит одновременно по
2-м направляющим, оставаясь в любой момент движения // некоторой плоскости,
называемой плоскостью параллелизма.
Слайд 17 Косая плоскость (гиперболический параболоид) – поверхность, у
которой обе направляющие прямые
Слайд 18
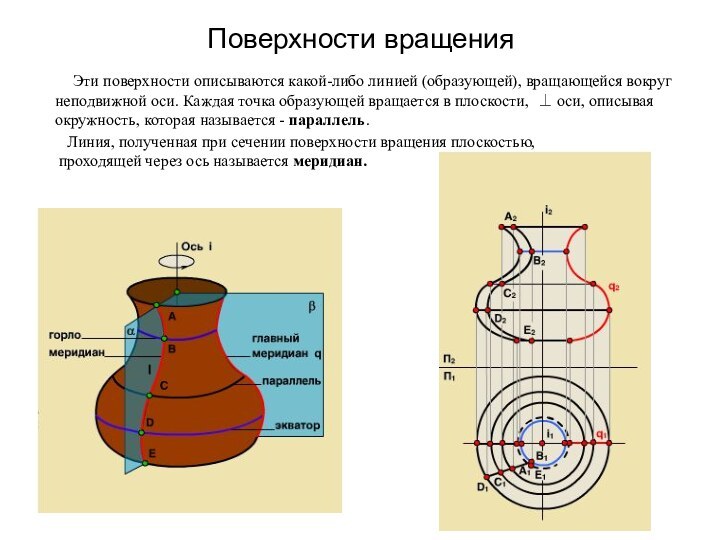
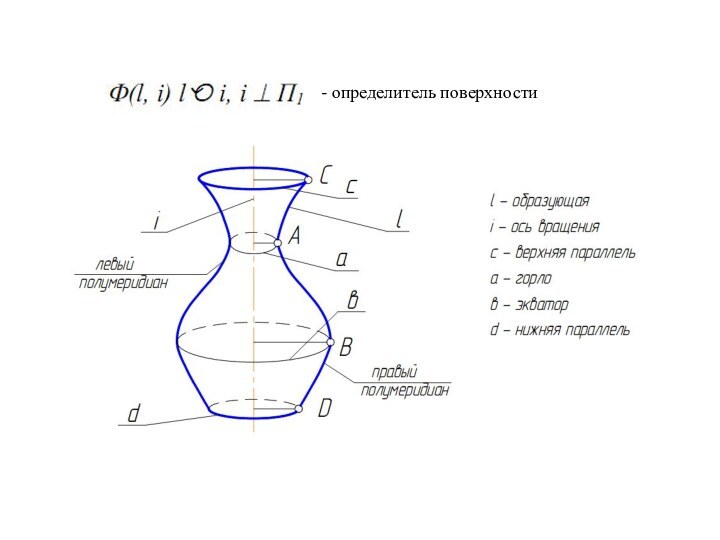
Поверхности вращения
Эти поверхности описываются какой-либо линией
(образующей), вращающейся вокруг неподвижной оси. Каждая точка образующей вращается
в плоскости, ⊥ оси, описывая окружность, которая называется - параллель. Линия, полученная при сечении поверхности вращения плоскостью,
проходящей через ось называется меридиан.
Слайд 21
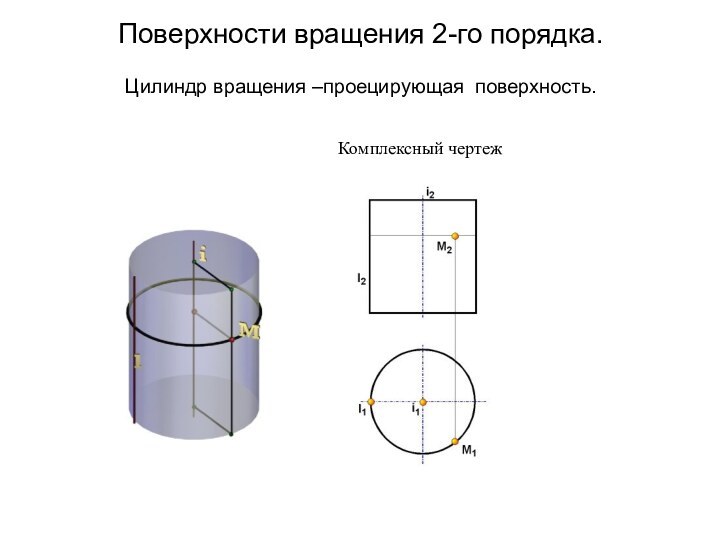
Поверхности вращения 2-го порядка.
Цилиндр вращения –проецирующая поверхность.
Комплексный
чертеж
Слайд 25
Однополостный гиперболоид вращения.
Комплексный чертеж.
Гипербола имеет две оси – действительную и мнимую. При
вращении гиперболы вокруг действительной оси – образуется однополостный гиперболоид вращения.Эта поверхность также может быть отнесена к линейчатым,
так как она может быть образована вращением
прямолинейной образующей вокруг скрещивающейся
с ней осью.
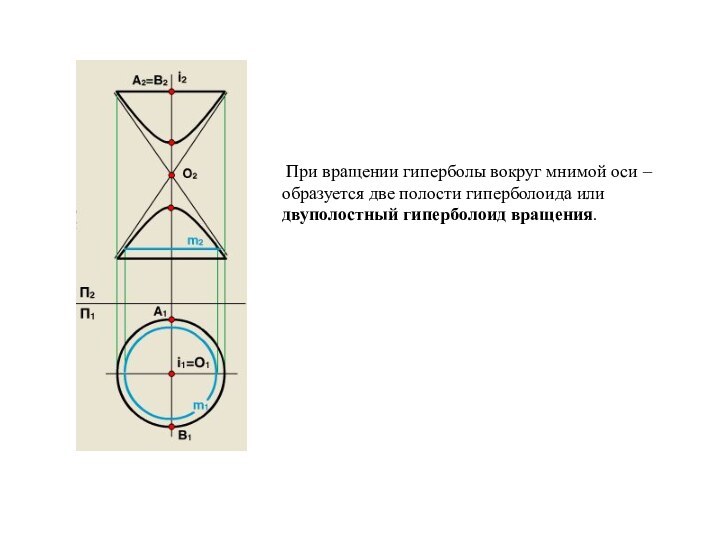
Слайд 26 При вращении гиперболы вокруг мнимой оси –
образуется две полости гиперболоида или двуполостный гиперболоид вращения.
Слайд 27
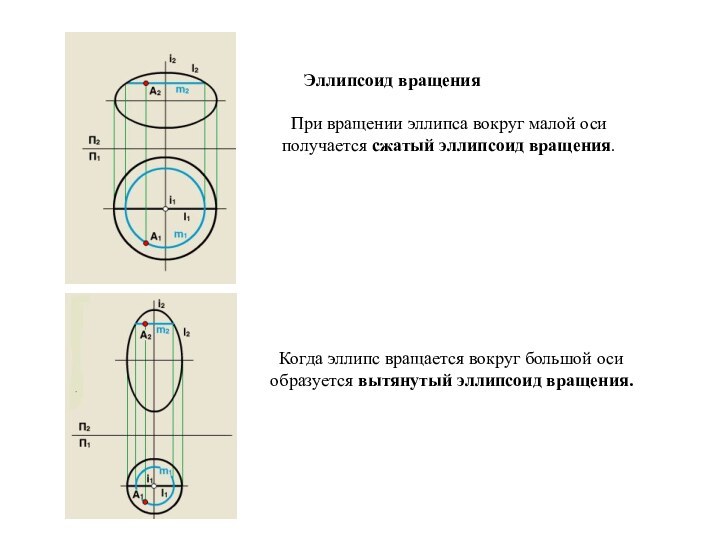
Эллипсоид вращения
При вращении эллипса
вокруг малой оси получается сжатый эллипсоид вращения.
Когда эллипс
вращается вокруг большой оси образуется вытянутый эллипсоид вращения.
Слайд 29
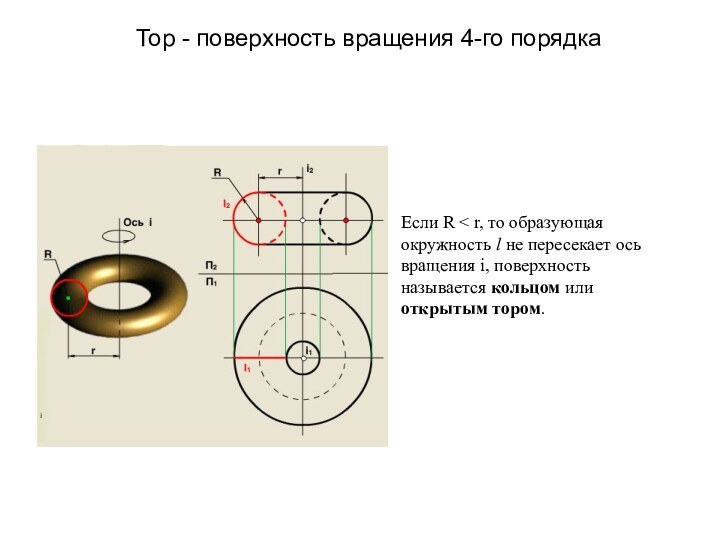
Тор - поверхность вращения 4-го порядка
Если R
r, то образующая окружность l не пересекает ось вращения
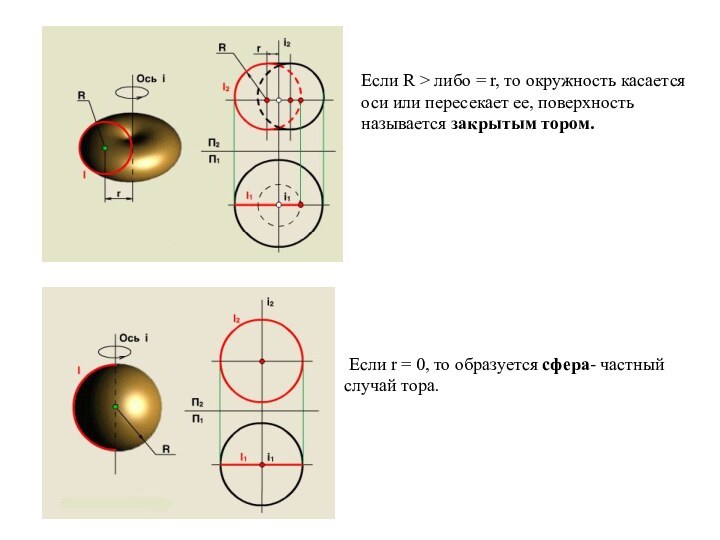
i, поверхность называется кольцом или открытым тором.Слайд 30 Если R > либо = r, то окружность
касается оси или пересекает ее, поверхность называется закрытым тором.
Если r = 0, то образуется сфера- частныйслучай тора.