- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Способы преобразования проекций (Лекция 3)
Содержание
- 2. Способы преобразования проекций
- 3. Способы преобразования проекций применяют для получения нового
- 5. Дополнительное прямоугольное проецирование – перемена плоскостей проекций
- 6. Подбираемая дополнительная плоскость проекций должна быть только
- 7. В ортогональной системе двух плоскостей проекций П1/П2 взята произво-льная точка А и построены ее проекции.
- 8. Введена дополнительная горизонтально-проецирующая плоскость проекций П4. Например,.
- 9. Точка А ортогонально проецируется на плоскость П4Так
- 10. Принцип построения эпюра при использовании способа перемены
- 11. Вращение
- 12. Каждая точка объекта вращается вокруг выбранной оси,
- 13. Ось вращения – прямая уровня
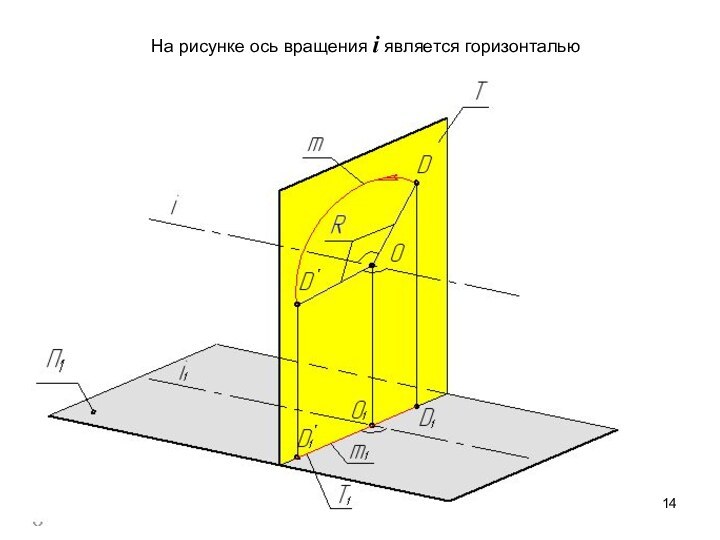
- 14. На рисунке ось вращения i является горизонталью
- 16. Базовые преобразования проекций
- 17. Рассматриваются два варианта преобразования.Вариант 1.
- 18. Базовое преобразование № 1.Преобразование прямой общего положения
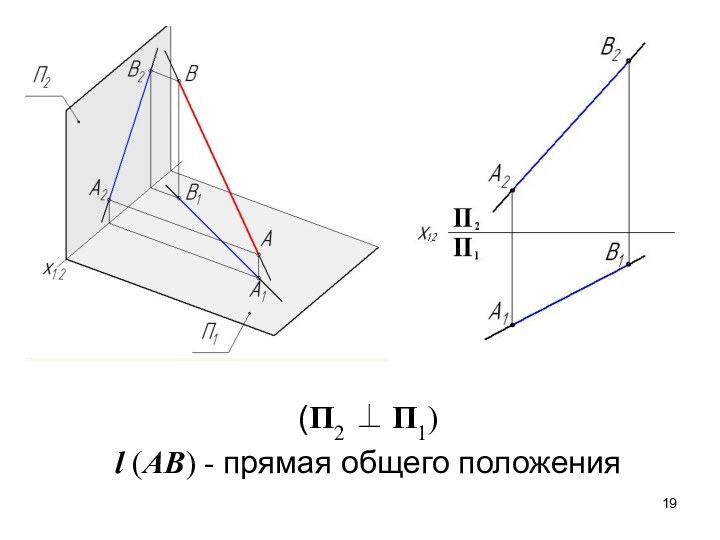
- 19. (П2 ⊥ П1) l (AB) - прямая общего положения
- 20. Подбирается дополнительная плоскость проекций П4( П4 ||
- 21. Строится дополнительная проекция l (AB) на поле
- 22. Базовое преобразование №2.Преобразование прямой общего положения в проецирующую прямую(построение дополнительной проекции прямой линии в виде точки)
- 23. При прямоугольном проецировании
- 24. 1-й этап Прямая преобразуется в прямую уровня
- 25. 2-й этап Из прямой уровня прямая
- 26. Для прямой уровня данное преобразование выполняется за
- 27. Базовое преобразование № 3. Преобразование плоскости (торсовой
- 28. Плоскость является проецирующей, если она перпендикулярна плоскости
- 29. (П4 ⊥ П1) ∨ (П4 ⊥ П2)Если
- 30. В качестве примера П4 ⊥ П1
- 32. Базовое преобразование № 4. Построение проекции плоской фигуры на параллельной ей плоскости проекций
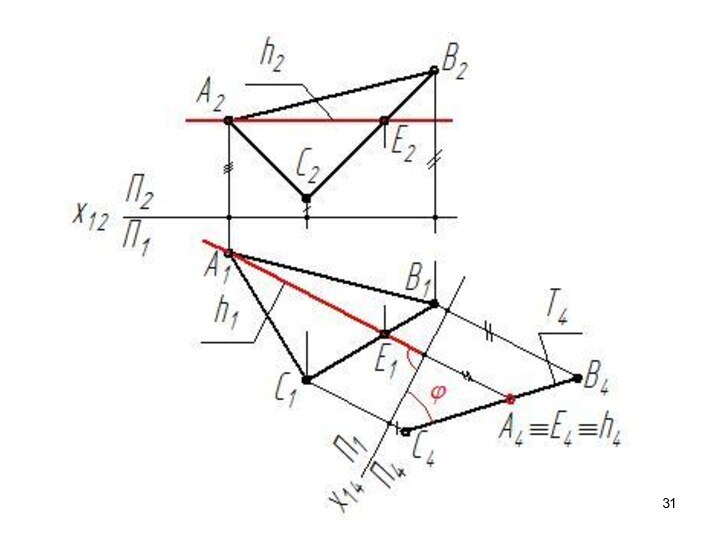
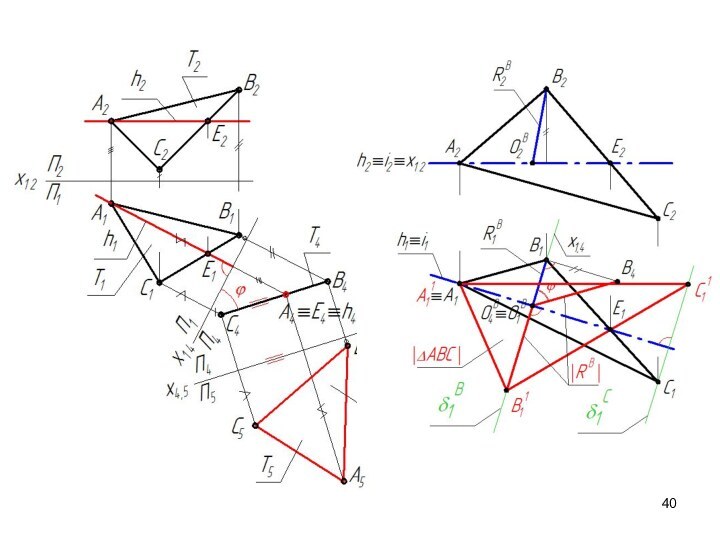
- 33. Решение задачи способом замены плоскостей проекций
- 34. П′ II ТТак как плоскость Т –
- 35. 1). П4 ⊥ Т(ΔАВС), П4 ⊥ П1
- 36. 1) П4 ⊥ Т(ΔАВС), П4 ⊥
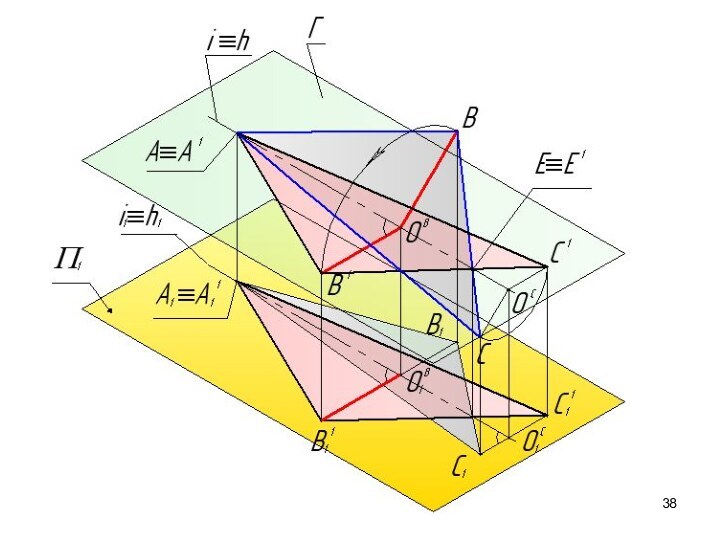
- 37. Решение задачи способом вращения вокруг прямой уровня
- 41. МЕТРИЧЕСКИЕ И КОНСТРУКТИВНЫЕ ЗАДАЧИ
- 42. Метрическими называются задачи, в ходе решения которых
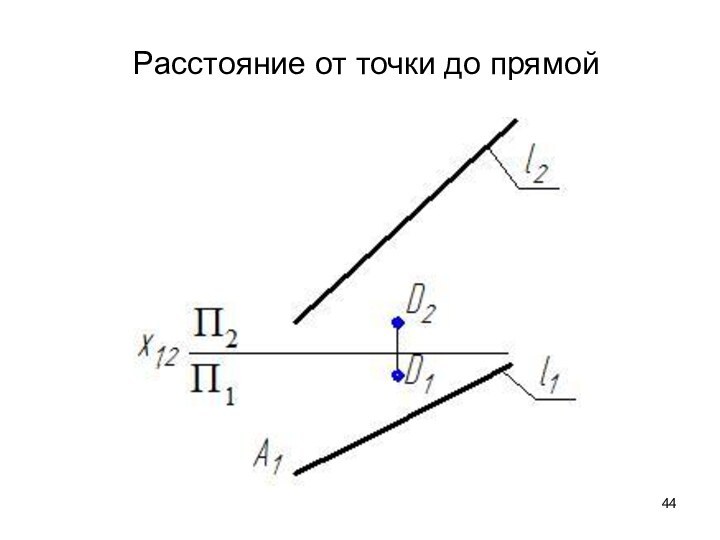
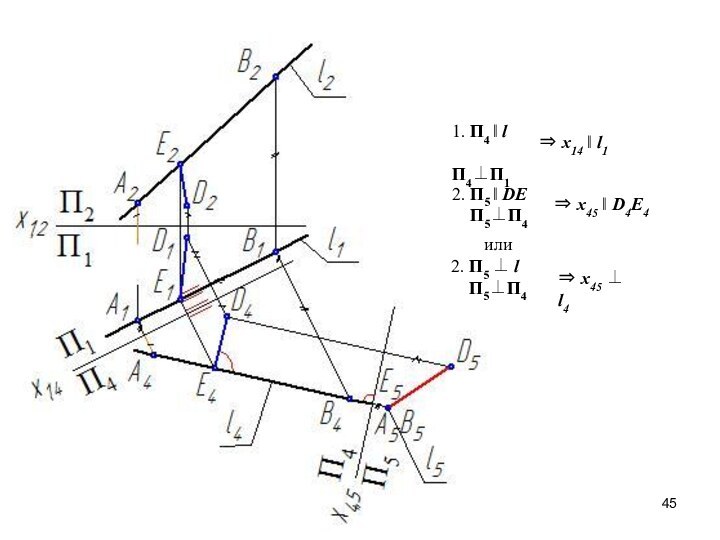
- 44. Расстояние от точки до прямой
- 45. 1. П4 ‖ l П4⊥П1⇒ х14
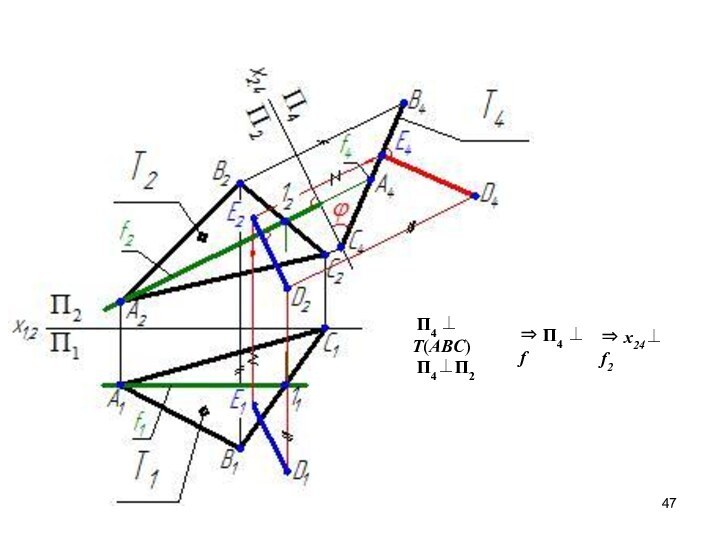
- 46. Расстояние от точки до плоскости
- 47. П4 ⊥ T(ABC) П4⊥П2⇒ П4 ⊥ f⇒ х24⊥ f2
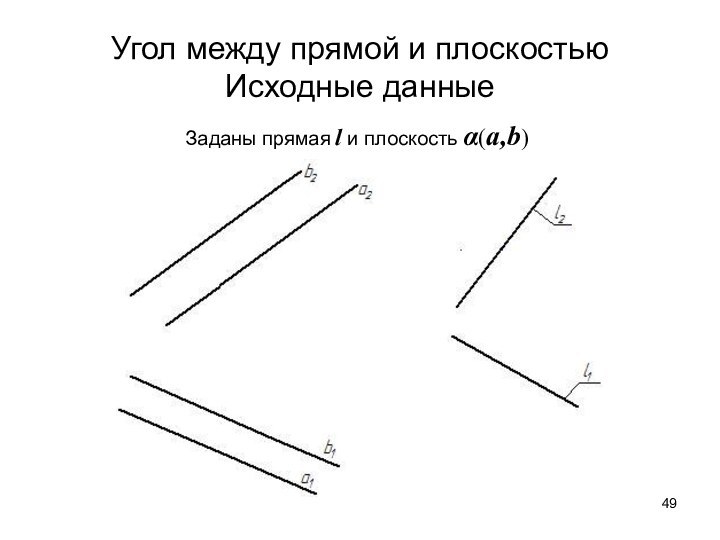
- 48. Угол между прямой и плоскостью∠ φ =
- 49. Угол между прямой и плоскостью Исходные данныеЗаданы прямая l и плоскость α(a,b)
- 50. 1. На прямой l выбирается произвольная точка
- 51. 3. В плоскости, образованной прямыми m и
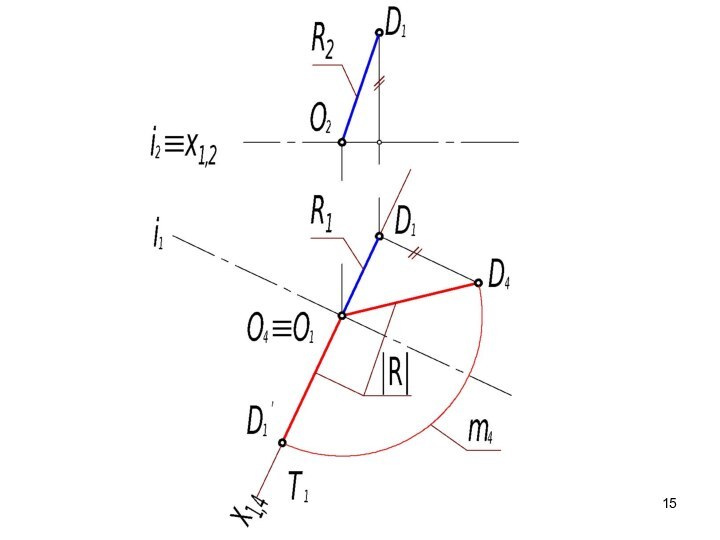
- 52. 6. Способом замены плоскостей проекций определяют истинную величину радиуса вращения точки D.
- 53. 7. Выполняют поворот точки D до совмещения
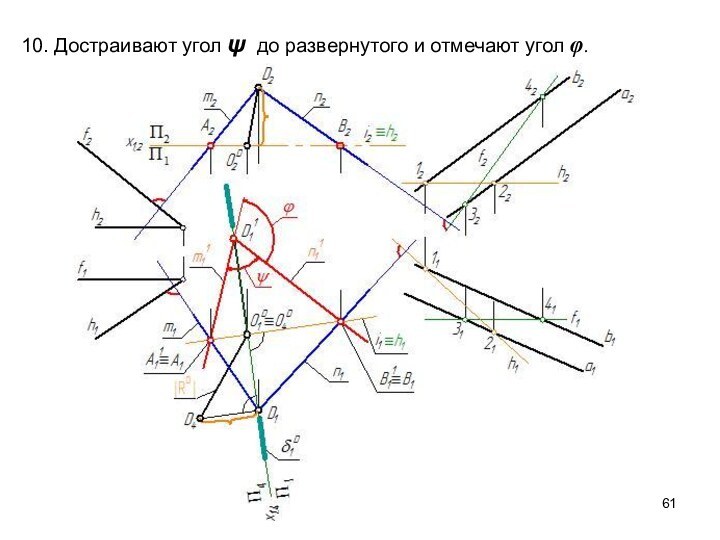
- 54. 10. Достраивают угол ψ до прямого и отмечают угол φ.
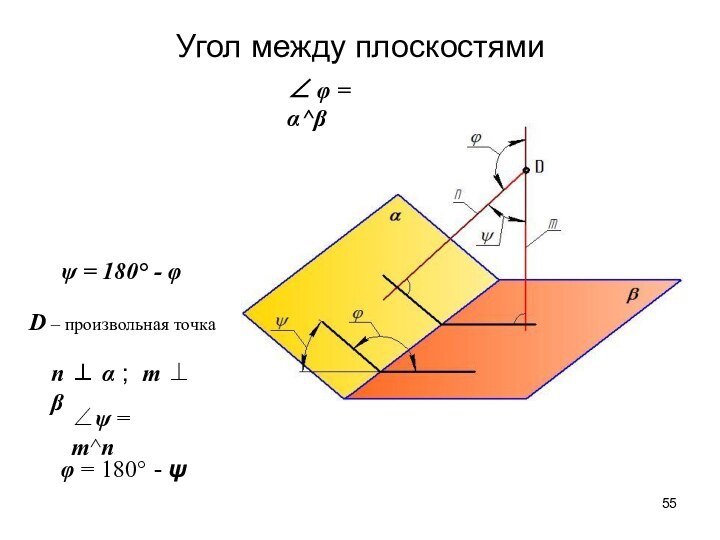
- 55. Угол между плоскостями∠ φ = α^βψ =
- 56. Угол между плоскостями Исходные данныеЗаданы плоскости α(h,f) и β(a,b)
- 57. 1. Вводится произвольная точка D.2. Через точку
- 58. 3. В плоскости, образованной прямыми m и
- 59. 6. Способом замены плоскостей проекций определяют истинную величину радиуса вращения точки D.
- 60. 7. Выполняют поворот точки D до совмещения
- 61. Скачать презентацию
- 62. Похожие презентации
Способы преобразования проекций























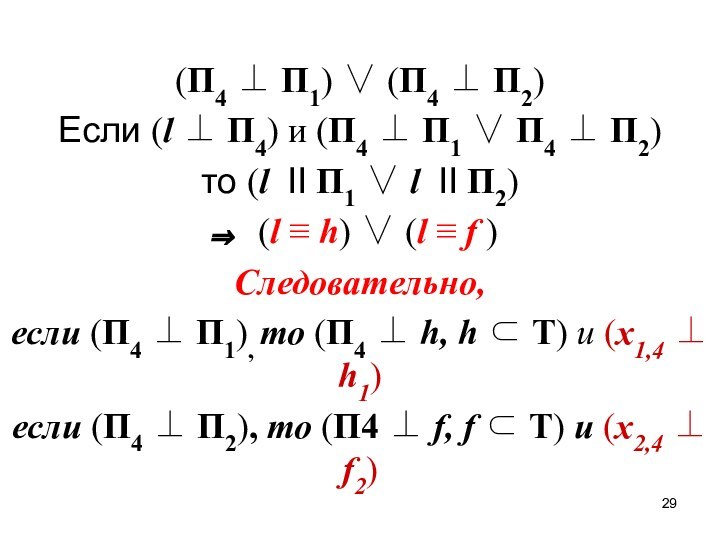























Слайд 6 Подбираемая дополнительная плоскость проекций должна быть только проецирующей.
Тем самым создаётся новая прямоугольная система плоскостей проекций.
Подбираемые дополнительные
плоскости проекций обозначаются П4, П5, П6 и т.д.Слайд 7 В ортогональной системе двух плоскостей проекций П1/П2 взята
произво-льная точка А и построены ее проекции.
Слайд 8 Введена дополнительная горизонтально-проецирующая плоскость проекций П4. Например,. Таким
образом создана новая система ортогональных плоскостей проекций П1/П4 с
осью х1,4 П4⊥ П1
П1∩ П4= х1,4
Х1,2 П1/П2
Х1,4 П1/П4
П1 - const
Слайд 9
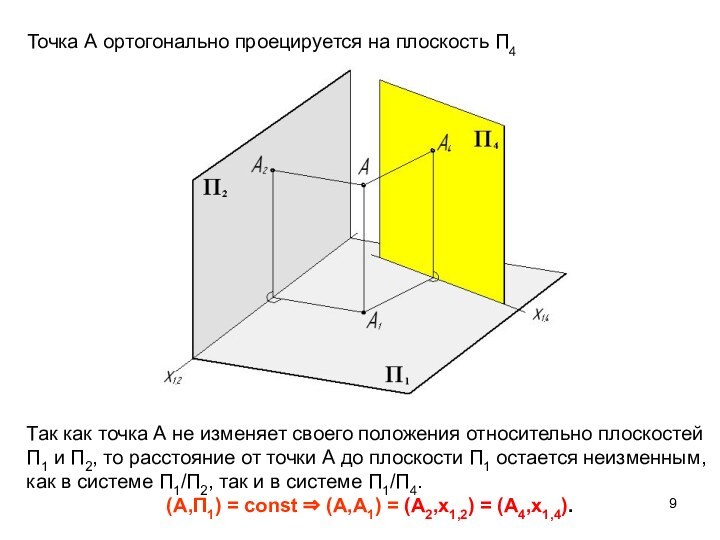
Точка А ортогонально проецируется на плоскость П4
Так как
точка А не изменяет своего положения относительно плоскостей
П1 и
П2, то расстояние от точки А до плоскости П1 остается неизменным, как в системе П1/П2, так и в системе П1/П4.
(А,П1) = const ⇒ (А,А1) = (А2,х1,2) = (А4,х1,4).
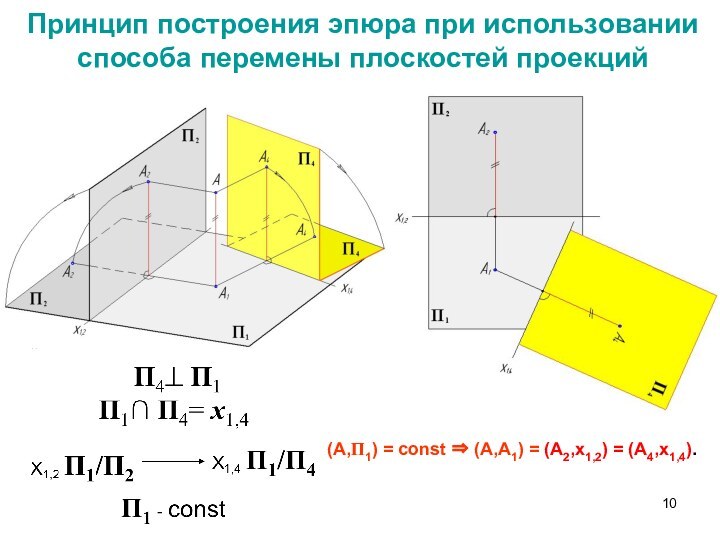
Слайд 10 Принцип построения эпюра при использовании способа перемены плоскостей
проекций
(А,П1) = const ⇒ (А,А1) = (А2,х1,2) = (А4,х1,4).
Слайд 12 Каждая точка объекта вращается вокруг выбранной оси, перемещаясь
по окружности, лежащей в плоскости перпендикулярной оси вращения.
Осью
вращения может быть только прямая частного положения – прямой уровня или проецирующей прямой.
Слайд 13
Ось вращения –
прямая уровня
Плоскость вращения
точки - проецирующую плоскость.
На плоскости проекций, параллельно
которой расположена ось вращения, траектория перемещения точки имеет форму прямой, а на другой – форму эллипса, что не дает возможности ее использования. Все построения выполняются только на одной проекции.
Вся задача сводится к определению истинной величины радиуса вращения точки.
Данный способ вращения имеет следующие ограничения:
- применим практически только к плоским фигурам;
- ось вращения должна лежать в плоскости поворачивае-
мой фигуры.
Слайд 17
Рассматриваются два варианта преобразования.
Вариант 1. Переход
от заданного положения объекта (прямой линии или плоской фигуры)
в параллельное положение по отношению к выбранной плоскости проекций.Вариант 2. Переход от заданного положения объекта (прямой линии или торсовой поверхности) в проецирующее положение по отношению к выбранной плоскости проекций.
Слайд 18
Базовое преобразование № 1.
Преобразование прямой общего положения в
прямую уровня
(построение дополнительной проекции прямой линии на параллельной
ей плоскости проекций)
Слайд 20
Подбирается дополнительная плоскость проекций П4
( П4 || l
) ∧ (( П4 ⊥ П1) ∨ (П4 ⊥
П2))На эпюре х14 || l 1 ∨ х24 || l 2
В качестве примера взята П4 ⊥ П1 , следовательно, х14 || l 1
Слайд 21 Строится дополнительная проекция l (AB) на поле плоскости
П4.
А1А4 ⊥ х1,4 и В1В4 ⊥ х1,4 ,
(А2х1,2)
= (А4х1,4) и (В2х1,2) = (В4х1,4)
Слайд 22
Базовое преобразование №2.
Преобразование прямой общего положения в проецирующую
прямую
(построение дополнительной проекции прямой линии в виде точки)
Слайд 23 При прямоугольном проецировании прямая
является проецирующей, если она перпендикулярна плоскости проекций. Следовательно, дополнительная
плоскость проекций должна быть перпендикулярна заданной прямойП′ ⊥ l ,
Но, так как l – прямая общего положения,
то П′ – также является плоскостью общего положения и П′ ⊥ П1 и П′ ⊥ П2 ,
Следовательно, чтобы получить проекцию прямой линии общего положения в виде точки способом перемены плоскостей проекций, нельзя сразу подобрать необходимую плоскость проекций.
Данное преобразование выполняется в два этапа.
Слайд 24 1-й этап Прямая преобразуется в прямую уровня ( П4
II l ) ∧ ( П4⊥ П1 ∨ П4⊥
П2 )Это рассмотренная ранее базовая задача №1 на построение проекции прямой общего положения на плоскости проекций ей параллельной.
Слайд 25 2-й этап Из прямой уровня прямая преобразуется в
проецирующую прямую ( П5 ⊥ l ) ∧ ( П5⊥
П4 )x4,5 ⊥ A4B4
(A1B1 , x1,4) = (A5B5 , x4,5)
Слайд 26 Для прямой уровня данное преобразование выполняется за один
этап
Прямая уровня (h или f) параллельна плоскости проекций.
Следовательно,
если П′ ⊥ (h или f), то П′ ⊥ (П1 или П2), что удовлетворяет требования способа перемены плоскостей проекций.
Слайд 27
Базовое преобразование № 3.
Преобразование плоскости (торсовой поверхности)
общего положения в проецирующую поверхность
(построение проекции плоскости в виде
прямой линии)
Слайд 28
Плоскость является проецирующей, если она перпендикулярна плоскости проекций.
Следовательно,
подбираемая новая плос-кость проекций П4 должна быть перпенди-кулярна заданной
плоскости, например Т.(П4 ⊥ Т)
Если плоскости взаимно перпендикулярны, то каждая из них должна содержать хотя бы одну прямую, перпендикулярную другой плоскости.
(П4 ⊥ Т) ⇒ (П4 ⊥ l ∧ l ⊂ Т)
Слайд 29
(П4 ⊥ П1) ∨ (П4 ⊥ П2)
Если (l
⊥ П4) и (П4 ⊥ П1 ∨ П4 ⊥
П2)то (l II П1 ∨ l II П2)
(l ≡ h) ∨ (l ≡ f )
Следовательно,
если (П4 ⊥ П1), то (П4 ⊥ h, h ⊂ Т) и (x1,4 ⊥ h1)
если (П4 ⊥ П2), то (П4 ⊥ f, f ⊂ Т) и (x2,4 ⊥ f2)
Слайд 32
Базовое преобразование № 4.
Построение проекции плоской фигуры
на параллельной ей плоскости проекций
Слайд 34
П′ II Т
Так как плоскость Т – плоскость
общего положения, то и любая плоскость ей параллельная, в
том числе и проекций П′, также будет плоскостью общего положения, т.е. П′ ⊥ П1 и П′ ⊥ П2, что противоречит способу замены плоскостей проекций. Следовательно, задача должна решаться в два этапа.1-й этап. П4 ⊥ Т (базовая задача №3).
2-й этап. П5 II Т.
Слайд 42 Метрическими называются задачи, в ходе решения которых определяется
значение измеряемой величины – расстояния между двумя точками (длина
отрезка), величины линейного угла или истинной формы и размеров плоской фигуры.Конструктивными называются задачи, в ходе решения которых создается геометрический объект по наперед заданным параметрам. В определенном смысле конструктивную задачу можно рассматривать как обратную метрической задаче.
Слайд 48
Угол между прямой и плоскостью
∠ φ = l^α
D
– произвольная точка
D ∈
l m ⊥ α
φ = 90° - ψ
∠ ψ = m^l
Слайд 50
1. На прямой l выбирается произвольная точка D.
2.
Через точку D проводят перпендикуляр к заданной плоскости. m⊥α
( m1⊥h1 m2⊥f2 )
Слайд 51 3. В плоскости, образованной прямыми m и l,
проводят горизонталь
(фронталь), которая является осью вращения
(h≡i).4. Задают плоскость вращения δ точки D вокруг оси i. δ 1 ⊥ i1
5. Отмечают центр вращения точки D – точку О.
Слайд 52
6. Способом замены плоскостей проекций определяют истинную
величину радиуса вращения точки D.
Слайд 53 7. Выполняют поворот точки D до совмещения с
плоскостью уровня,
в которой расположена ось вращения.
8.
Проводят новые проекции m1 и l1 прямых m и l.9. Отмечают угол ψ, образованный прямыми m1 и l1.
Слайд 55
Угол между плоскостями
∠ φ = α^β
ψ = 180°
- φ
D – произвольная точка
n ⊥ α ; m
⊥ β∠ψ = m^n
φ = 180° - ψ
Слайд 57
1. Вводится произвольная точка D.
2. Через точку D
проводят перпендикуляры к каждой из заданных
плоскостей.
m⊥α n⊥β( l1⊥h1 l2⊥f2 )
Слайд 58 3. В плоскости, образованной прямыми m и n,
проводят горизонталь
(фронталь), которая является осью вращения
(h≡i).4. Задают плоскость вращения δ точки D вокруг оси i. δ 1 ⊥ i1
5. Отмечают центр вращения точки D – точку О.
Слайд 59
6. Способом замены плоскостей проекций определяют истинную
величину радиуса вращения точки D.
Слайд 60 7. Выполняют поворот точки D до совмещения с
плоскостью уровня,
в которой расположена ось вращения.
8.
Проводят новые проекции m1 и n1 прямых m и n.9. Отмечают угол ψ, образованный прямыми m1 и n1.