Слайд 2
В ходе исследования предстоит решить проблему: как влияет
использование логических игр на развитие математических способностей старших дошкольников?
Цель – развитие математических способностей старших дошкольников путем использования логико-математических игр.
Объект исследования – элементарные математические представления у старших дошкольников; предмет исследования – логические игры при формировании элементарных математических представлений у дошкольников.
Гипотеза исследования: использование логических игр в процессе обучения способствуют повышению уровня сформированности элементарных математических представлений у старших дошкольников.
Слайд 3
Задачи исследования:
1. Проанализировать психолого-педагогическую литературу по данной проблеме.
2.
Дать общую характеристику содержания понятия «формирование элементарных математических представлений
3.
Разработать систему занятий по формированию элементарных математических представлений с использованием логических игр.
4. Исследовать эффективность использования логических игр в процессе формирования элементарных математических представлений у старших дошкольников
Слайд 4
Математическое развитие состоит из взаимосвязанных и взаимообусловленных представлений

о пространстве, форме, величине, количестве, их свойствах и отношениях,
которые необходимы для формирования у ребенка «житейских» и «научных» понятий. (Носова Е.А.)
Под математическим развитием дошкольников, следует понимать «сдвиги и изменения познавательной деятельности личности, которые происходят в результате формирования математических представлений и связанных с ними логических операций» (А.А. Столяра, Р.Л. Непомнящей, Е.И. Щербаковой )
А.В. Белошистая под математическим развитием ребенка предлагает понимать «целенаправленное и методически организованное формирование и развитие совокупности взаимосвязанных основных свойств и качеств математического мышления ребенка и его способностей к математическому познанию действительности»
В настоящее время встречается понятие «логико-математическое развитие», которое является идентичным понятию «математическое развитие» (З.А.Михайлова, А.М. Вербенец и др.).
В 60-70 годах 20 века начался активный поиск новых подходов к содержанию математического развития дошкольников, а также средств, форм и способов его реализации. Достоянием этого периода следует признать разработку и популяризацию развивающих игр Б. П. Никитиным и обучающих логико-математических игр А. А. Столяром, Р. Ф. Соболевским, Н. К. Рузиным,
Е.А. Носовой, З.А. Михайловой.
Слайд 5
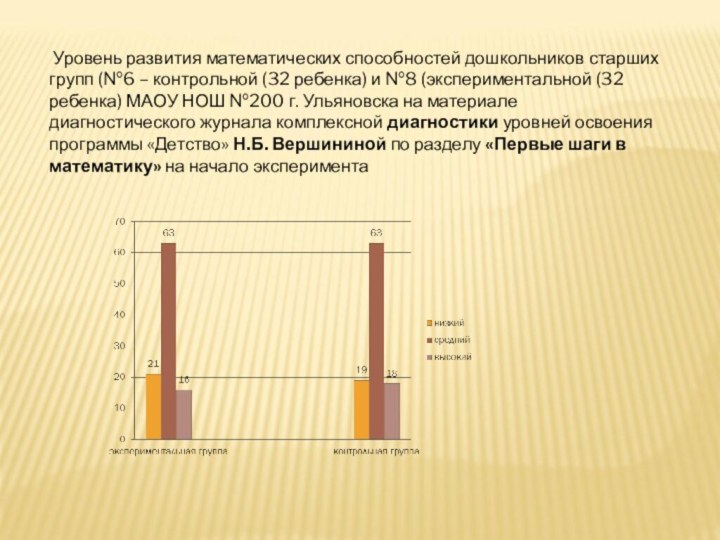
Уровень развития математических способностей дошкольников старших групп
(№6 – контрольной (32 ребенка) и №8 (экспериментальной (32
ребенка) МАОУ НОШ №200 г. Ульяновска на материале диагностического журнала комплексной диагностики уровней освоения программы «Детство» Н.Б. Вершининой по разделу «Первые шаги в математику» на начало эксперимента
Слайд 6
Так как важным средством формирования мыслительной деятельности ребёнка,
его интеллекта является игра, то в дошкольной педагогике существует
множество разнообразных методических материалов: методик, технологий, которые обеспечивают интеллектуальное развитие детей это: логические блоки Дьенеша, палочки Кюизенера, кубики Никитина и игры-головоломки.
Слайд 7
Логические блоки Дьенеша представляют собой игры, составленные на
основе комплекта, который состоит из 48 геометрических фигур четырех
форм (круги, треугольники, квадраты, прямоугольники); трех цветов (красные, синие и желтые); двух размеров (большие, маленькие); двух объемов (толстые, тонкие). Каждая геометрическая фигура характеризуется четырьмя признаками: формой, цветом, размером, толщиной. Вторая составляющая игры – карточки, на которых закодирована информация о геометрической фигуре и ее признаках. Одни кодовые карточки разделены на две части: первая указывает на то, какую геометрическую фигуру (логический блок) мы ищем; вторая содержит информацию о том, какого цвета эта фигура. На следующих карточках к указанной информации добавляются такие понятия, как величина геометрической фигуры и ее толщина.
Слайд 8
Танграм - старинная восточная головоломка из фигур, получившихся
при разрезании квадрата на 7 частей особым образом В
результате складывания этих частей друг с другом получаются плоские фигуры, контуры которых напоминают всевозможные предметы. Такого рода головоломки часто называют "геометрическими конструкторами“.
Слайд 9
В играх удается соединить один из основных принципов
обучения – от простого к сложному – с очень
важным принципом творческой деятельности самостоятельно по способностям, когда ребенок может подняться до «потолка» своих возможностей.
Решение задачи предстает перед ребенком не в абстрактной форме ответа логической задачи, а в виде рисунка, узора или сооружения из кубиков, деталей конструктора, т. е. в виде видимых и осязаемых вещей. Это позволяет сопоставлять наглядно «задание» с «решением» и самому проверить точность выполнения задания.
Слайд 10
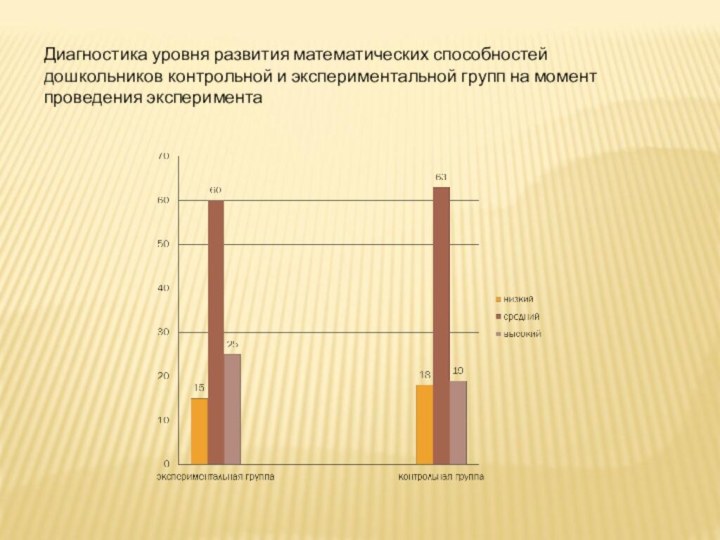
Диагностика уровня развития математических способностей дошкольников контрольной и
экспериментальной групп на момент проведения эксперимента