Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Эконометрика

Содержание

2. Коэффициент эластичностиДля сопоставления факторов по степени влияния
3. Технология построения модели множественной линейной регрессии в
4. Пример: Пусть по данным бюджетного обследования случайно
5. 2) Сервис – Анализ данных –
6. 4) Оцениваем значимость каждого из полученных
7. Если P-значение коэффициента bi > 5%,
8. 5) Если после того, как отобраны только
9. Пример: Приведены результаты исследования, посвященное изучению того,
10. Нелинейная регрессия.
11. Во многих случаях даже графическое представление
12. Типы нелинейных моделей:Модели нелинейные по переменным, но
13. 1 тип:1.1
14. 2 тип:2.1
15. Для того, чтобы оценить неизвестные параметры a,
16. Способы линеаризации1.1 Пусть имеем выборку { yi
17. 1.2 Исходная выборка { yi , xi
18. Скачать презентацию
19. Похожие презентации

Коэффициент эластичностиДля сопоставления факторов по степени влияния на зависимую переменную используются частные коэффициенты эластичности Эi:Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная y при изменении фактора i на 1%.

Технология построения модели множественной линейной регрессии в Excel1) Строим матрицу парных корреляций,

Пример: Пусть по данным бюджетного обследования случайно выбранных семей изучалась зависимость накопления

2) Сервис – Анализ данных – Регрессия. В качестве Входного

4) Оцениваем значимость каждого из полученных коэффициентов a, b1, b2, …

Если P-значение коэффициента bi > 5%, то с надежностью 95% принимаем

5) Если после того, как отобраны только значимые факторы, показатели R2 ,

Пример: Приведены результаты исследования, посвященное изучению того, какие факторы существенно влияют на цену

Во многих случаях даже графическое представление данных показывает, что интересующая нас

Типы нелинейных моделей:Модели нелинейные по переменным, но линейные по параметрам.Модели нелинейные как

Для того, чтобы оценить неизвестные параметры a, b, c необходимо привести модель

Способы линеаризации1.1 Пусть имеем выборку { yi , xi } , i

1.2 Исходная выборка { yi , xi } , i = 1

1.3 Исходная выборка { yi , xi } , i = 1

Слайды презентации

Слайд 2 Коэффициент эластичности
Для сопоставления факторов по степени влияния на

Коэффициент эластичностиДля сопоставления факторов по степени влияния на зависимую переменную используются

зависимую переменную используются частные коэффициенты эластичности Эi:

Коэффициент эластичности показывает,

на сколько процентов изменяется зависимая переменная y при изменении фактора i на 1%.

Слайд 3 Технология построения модели множественной линейной регрессии в Excel
1)

Технология построения модели множественной линейной регрессии в Excel1) Строим матрицу парных

Строим матрицу парных корреляций, чтобы определить силу влияния каждого

фактора на y и тесноту межфакторных связей:
Excel 2003: Сервис – Анализ данных – Корреляция
Excel 2007: Данные – Анализ данных – Корреляция

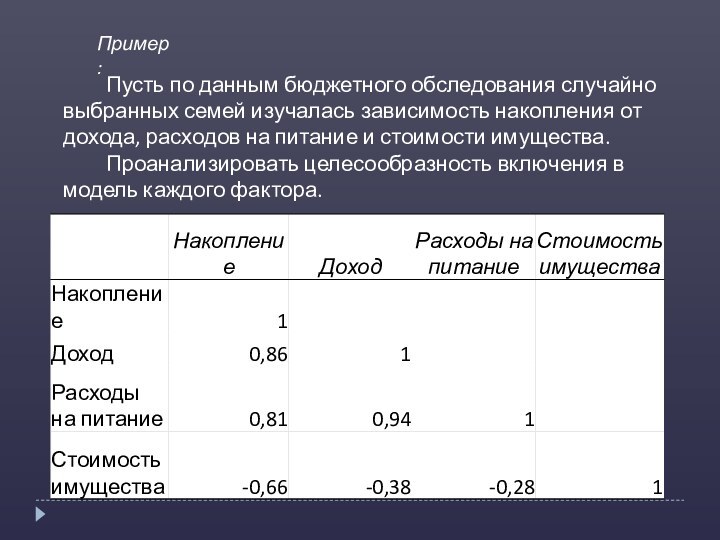
Слайд 4 Пример:
Пусть по данным бюджетного обследования случайно выбранных

Пример: Пусть по данным бюджетного обследования случайно выбранных семей изучалась зависимость

семей изучалась зависимость накопления от дохода, расходов на питание

и стоимости имущества.
Проанализировать целесообразность включения в модель каждого фактора.

Слайд 5 2) Сервис – Анализ данных – Регрессия.

2) Сервис – Анализ данных – Регрессия. В качестве Входного интервала

В качестве Входного интервала X выделить все столбцы xi

одновременно.
3) Оцениваем тесноту связи между результатом и факторами по ρ, качество уравнения регрессии по R2, статистическую значимость коэффициента детерминации R2 по F-значению. Схема проверки, как и в модели парной линейной регрессии.

Слайд 6 4) Оцениваем значимость каждого из полученных коэффициентов

a, b1, b2, … bn по их P-значениям:
Если

коэффициент bi имеет P-значение < 5%, то этот коэффициент статистически значим и включается в модель.

Слайд 7 Если P-значение коэффициента bi > 5%, то

Если P-значение коэффициента bi > 5%, то с надежностью 95%

с надежностью 95% принимаем нуль-гипотезу о статистической незначимости bi

( bi = 0 для всей генеральной совокупности), делаем вывод что фактор xi не влияет на изменение y, и перестраиваем модель, исключив из исходного набора данных фактор xi.
Если таких факторов оказалось несколько, то следует удалять их из модели по одному, каждый раз перестраивая модель МЛР. Первым следует удалить тот фактор, у которого P-значение максимально.

Слайд 8 5) Если после того, как отобраны только значимые

факторы, показатели R2 , ρ, значимость F неудовлетворительны, следует

попробовать:
удалить статистические выбросы;
перейти к нелинейной модели;
добавить наблюдения в выборку.
6) Сравнить полученную модель с матрицей парных корреляций. Совпадают ли выводы о влиянии факторов на y и друг на друга по матрице и построенной модели.

Слайд 9 Пример:
Приведены результаты исследования, посвященное изучению того, какие

Пример: Приведены результаты исследования, посвященное изучению того, какие факторы существенно влияют

факторы существенно влияют на цену журнала.
Пусть y - цена одного

экземпляра журнала (руб.)

Слайд 10 Нелинейная регрессия.

Слайд 11 Во многих случаях даже графическое представление данных

Во многих случаях даже графическое представление данных показывает, что интересующая

показывает, что интересующая нас зависимость не может быть описана

прямой линией.
В этом случае для исследования зависимости между x и y применяются нелинейные функции.

Слайд 12 Типы нелинейных моделей:
Модели нелинейные по переменным, но линейные

Типы нелинейных моделей:Модели нелинейные по переменным, но линейные по параметрам.Модели нелинейные

по параметрам.
Модели нелинейные как переменным, так и по параметрам.

Слайд 13 1 тип:
1.1

- гиперболическая
1.2 - логарифмическая
1.3 - параболическая ( если степень >2, то полиномиальная)

Слайд 14 2 тип:
2.1

степенная
2.2 экспоненциальная
2.3 обратная

Слайд 15 Для того, чтобы оценить неизвестные параметры a, b,

Для того, чтобы оценить неизвестные параметры a, b, c необходимо привести

c необходимо привести модель к линейному виду, иначе говоря

линеаризовать.
Линеаризация- преобразование нелинейной модели к линейной, путем замены переменной.
После такого преобразования можно применить метод наименьших квадратови найти коэффициенты регрессии.

Слайд 16 Способы линеаризации
1.1 Пусть имеем выборку { yi ,

Способы линеаризации1.1 Пусть имеем выборку { yi , xi } ,

xi } , i = 1 … n.
Необходимо построить

модель

Делаем замену переменных
Новая выборка { yi , vi } . По ней строим модель y = a + b · v. Находим a и b по МНК и подставляем найденные коэффициенты в исходную модель