Слайд 2
Методы теории игр для анализа поведения олигополии
Теория игр
- наука, которая исследует математическими методами поведение участников в
вероятностных ситуациях связанных с принятием решений.
Простейшим изображения игры является матрица результатов. Матрица результатов - двухсторонняя таблица, образованная множеством квадратов, каждый из которых представляет результат стратегического взаимодействия обоих участников.
Слайд 3
Классификация игр по свойствам платежных функций
Игры с нулевой
суммой (антагонистические) - ситуация, когда выигрыш одного из игроков
равен проигрышу другого. Противоположностью играм с нулевой суммой являются игры с постоянной разностью, в которых игроки выигрывают и проигрывают одновременно, так что им выгодно действовать сообща. Игры с ненулевой суммой представляют собой промежуточный случай, где имеются конфликты и согласованные действия игроков.
Слайд 4
Классификация игр по характеру предварительной договоренности
кооперативные (когда
существует сговор);
некооперативные (когда каждый за себя).
Например, уже известная нам
модель Курно представляет собой некооперативную игру с ненулевой суммой.
Слайд 5
Матрица результатов ценовой конкуренции
Слайд 6
Варианты решений
Если фирмы будут конкурировать, то положение равновесия
будет достигнуто в квадрате D, где прибыль каждого будет
равна нулю. Такое решение получило название равновесия Нэша.
Равновесием Нэша называется такое решение игры, от которого нет оснований отказываться ни одному из игроков в одиночку.
В случае конкуренции рассмотренный случай соответствует уже известной нам модели Бертрана.
Если продавцы договариваются между собой, т.е. образуют картель, то этот сговор приносит им максимальную прибыль, которая представлена в квадрате А.
Слайд 7
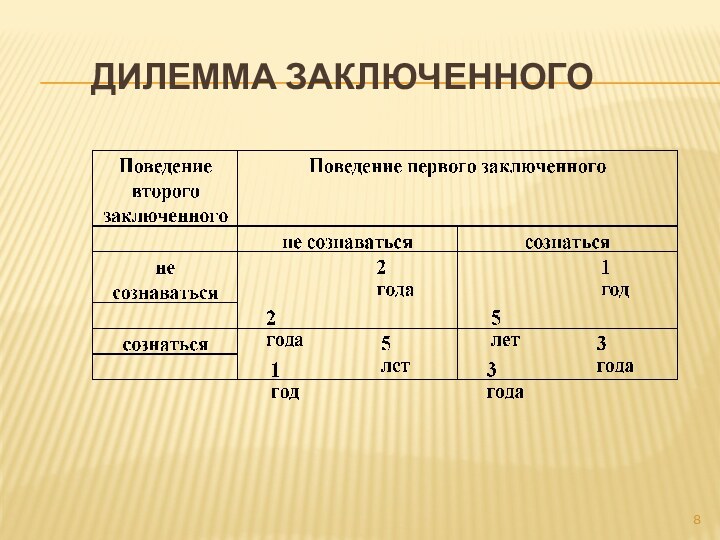
Дилемма заключенного
Дилемма заключенного является одним из вариантов матрицы
результатов и заключается в следующем:
два заключенных поставлены перед
дилеммой, либо они не сознаются в преступлении и тогда получают по два года заключения каждый, либо сознается кто-то один, который за признание отправляется в тюрьму на один год, но другой получает 5 лет. Если они сознаются оба, то получают оба по 3 года.
Вся проблема заключается в том, что каждый поставлен перед своей дилеммой отдельно.
Слайд 9
Дилемма заключенного
Наиболее вероятное решение в этом случае может
быть достигнуто в квадрате D, когда каждый получит по
3 года. Но этот результат вероятен, если они не могут между собой договориться. Если сговор возможен, то они получают по 2 года.
По аналогии с продавцами, ситуация демонстрирует желание продавцов вступать в сговор на рынке для достижения наиболее благоприятного для каждого из них результата, вместо того чтобы конкурировать и снижать свои прибыли до минимума (квадрат D).
Слайд 10
Исходные данные примера более сложной модели
Предположим, что есть
два игрока А и В. Каждый игрок осуществляет выбор
в зависимости от стратегии другого игрока.
Предполагается, что игра является антагонистической с нулевой суммой.
Игроку А доступны стратегии a1, a2, a3; игроку B – стратегии b1, b2.
Матрицы выигрышей игроков А и В представлены в таблицах (выигрыш игрока А равен проигрышу игрока В).
Слайд 13
Поиск стратегий
Обозначив A(bi) - выбор игрока A в
зависимости от выбора стратегии игрока В, а B(aj) –
выбор игрока В в зависимости от стратегии игрока А, можно заключить следующее.
Слайд 14
Возможные стратегии
Игроку А доступны следующие решения в зависимости
от стратегии В:
А игроку В следующие:
Таким образом здесь
нет равновесия Нэша.
Слайд 15
Матрица выигрышей игрока А – измененные исходные данные
Слайд 16
Возможные стратегии
Игроку А доступны следующие решения в зависимости
от стратегии В:
А игроку В следующие:
Таким образом равновесие Нэша
будет наблюдаться тогда, когда Игроки А и В выберут стратегии a3 и b2 соответственно.