Слайд 2
План лекции
1. Характеристики.
2. Модели ценообразования
21. Ломаная кривая
спроса
2.2. Модели количественные
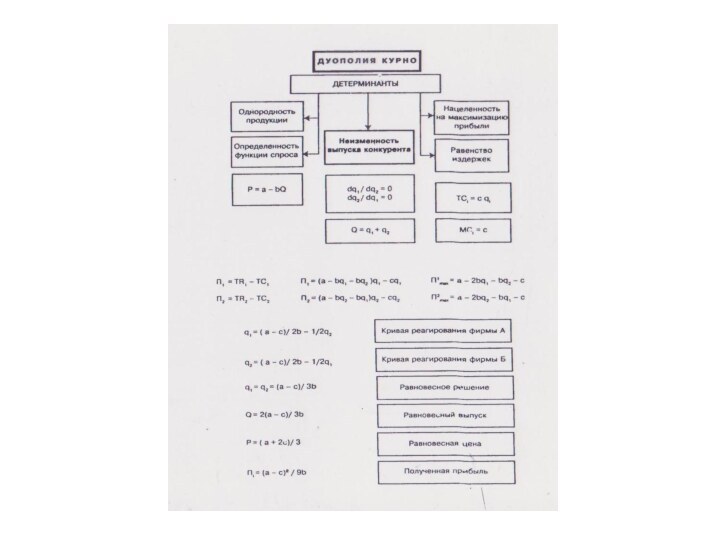
2.2.1 Модель Курно
2.2.2. Модель Чемберлина
2.2.3. Модель Штакильберга
2.3.
Ценовые модели
2.3.1. Модель Бертрана
2.3.2. Модель Эджуорта
2.з.3. Лидерство в ценах Модель Форхаймера
2.4 Картель
Слайд 3
Характеристики
Количество фирм – несколько
Тип товара –однородный и дифференцированный
Влияние
на цену – сильное, но стратегическое, взаимозависимое
Существуют значительные барьеры
входа-выхода в отрасль (юридические, экономические, географические)
Слайд 7
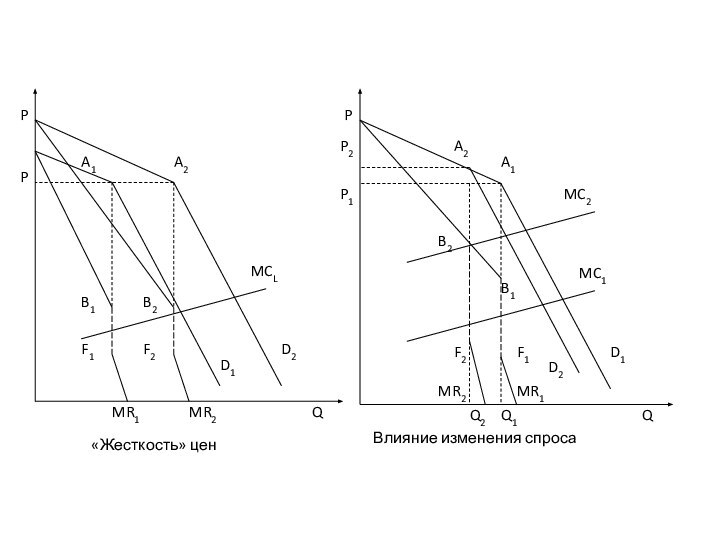
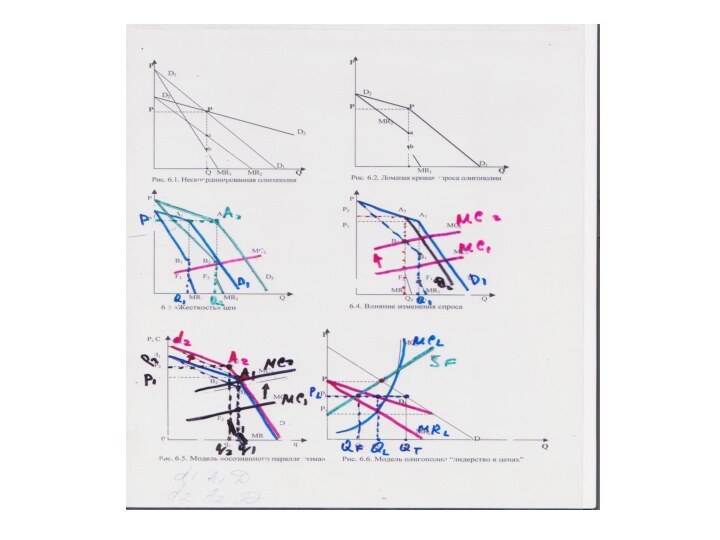
Ломаная кривая спроса олигополии
Нескоординированная олигополия
Слайд 16
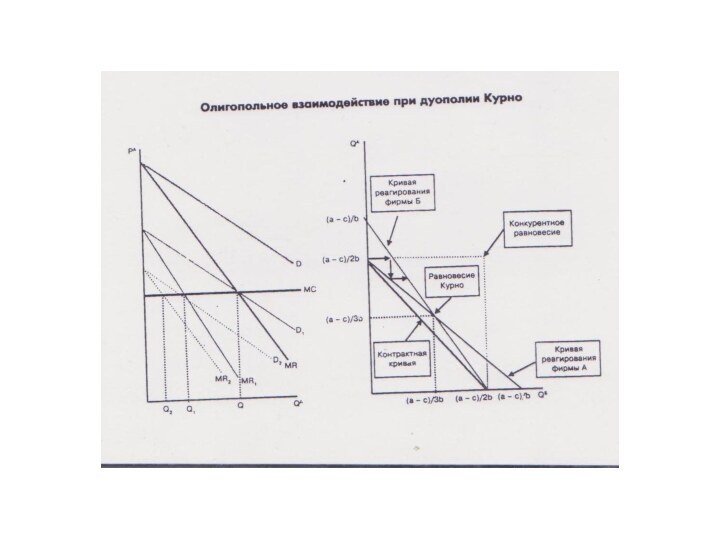
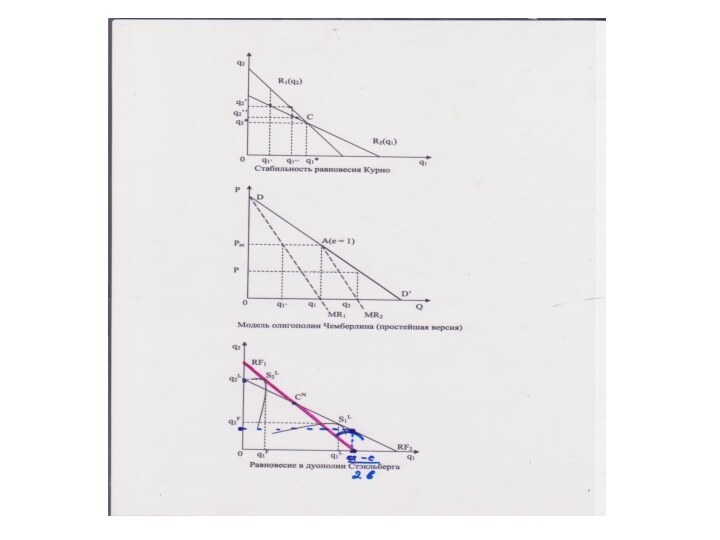
Устойчивость равновесия в дуополии Курно
Слайд 18
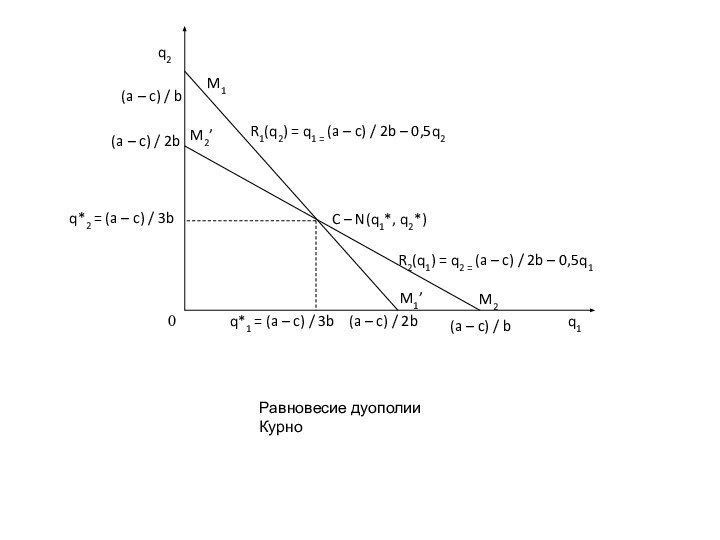
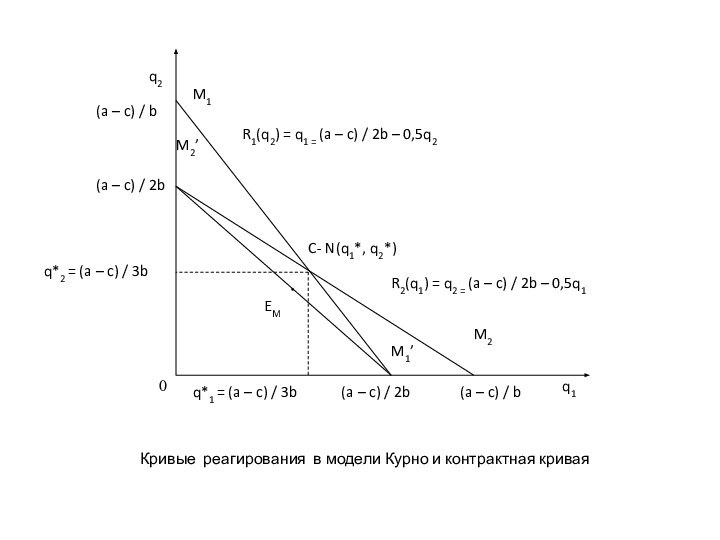
Кривые реагирования в модели Курно и контрактная кривая
Слайд 19
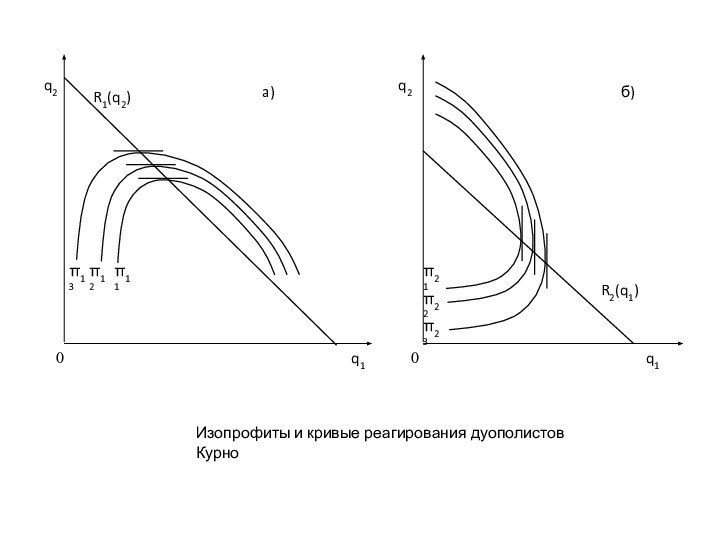
Изопрофиты и контрактная кривая
Слайд 20
Модель Чемберлина
В Модели Чемберлина (1956г.) в отличие от
модели Курно дуополист предполагает, что уровень выпуска конкурента изменяется
в ответ на его решения. В итоге дуополисты, не вступая в тайный сговор, выберут для себя наиболее выгодные для себя решения (рис.6.16 ). Примем, что МС1=МС2=0
Слайд 21
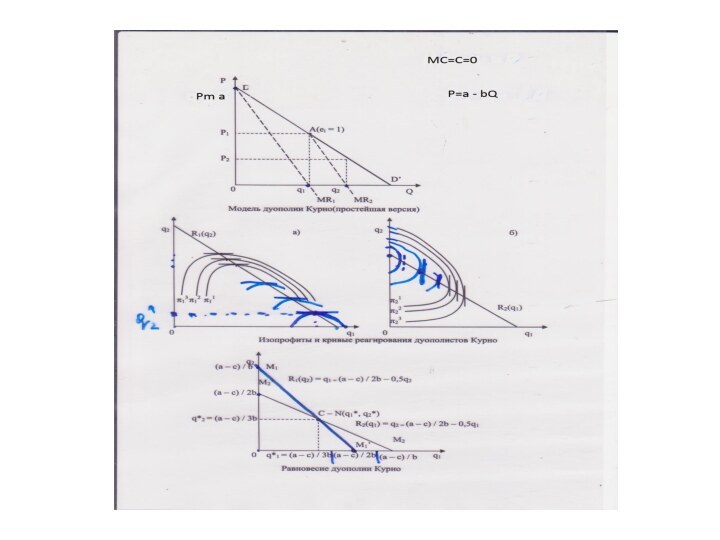
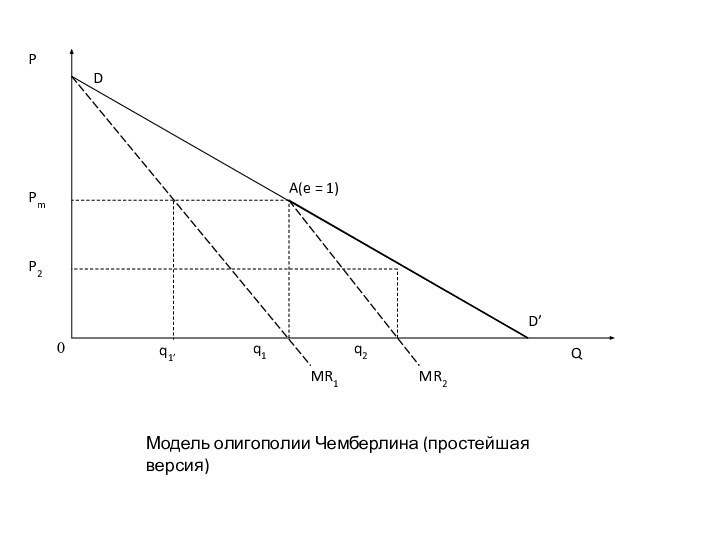
Модель олигополии Чемберлина (простейшая версия)
Слайд 22
Модель Чемберлина
Первый шаг. Пусть первая фирма ведет себя
как монополист. Максимизируя прибыль она выберет объем производства и
цену:
q1=Qm=(а-с)/2b
Рm==(а+с)/2 При этом прибыль составит:
П1= (а – с)2/4 bq
Слайд 23
Модель Чемберлина
Второй шаг. Вторая фирма, принимая решение, исходит
уже из остаточной функции спроса АD’, считая что выпуск
первой фирмы не изменится. Вторая фирма на остаточном спросе также принимает решение как монополист. Остаточную функцию спроса можно рассмотреть как функцию рыночного спроса, но только в новой системе координат, смещенной по отношению к первоначальной на q1. Уравнение остаточной функции спроса:
Р’=(а+с)/2-bq2
Максимизируя прибыль вторая фирма будет производить ровно половину от монопольного выпуска первой фирмы:
q2=(а-с)/4b
В итоге при снижении цены до:
Р=(а+3с)/4
отраслевой объем выпуска составит:
Q=3(а-с)/4b
Поскольку уже в результате второго шага рыночная цена снизилась, прибыль первой фирмы составит всего лишь половину от первоначальной монопольной прибыли:
П1= (а – с)2/8 b,
а у второй фирмы – еще меньше:
П2= (а – с)2/16 b.
Слайд 24
Модель Чемберлина
Поскольку мы предположили существование линейной функции спроса
р=а-2bQ и однородность выпускаемой продукции (поэтому q1=q2=q), то функция
спроса примет вид:
р=а-2
А поскольку мы считали, что издержки равны, то функция прибыли:
П= а q– 2bq2 -сq,
Необходимое условие максимизации прибыли:
dП/dq= а – 4bq - с=0
Достаточное условие максимизации прибыли
d2П/d2q= – 4b<0 Вывод: если выполняются предпосылки о равных издержках и однородности продукции, то фирмы в модели Чемберлина не вступая в тайный сговор, установят на рынке монопольную цену.
Слайд 26
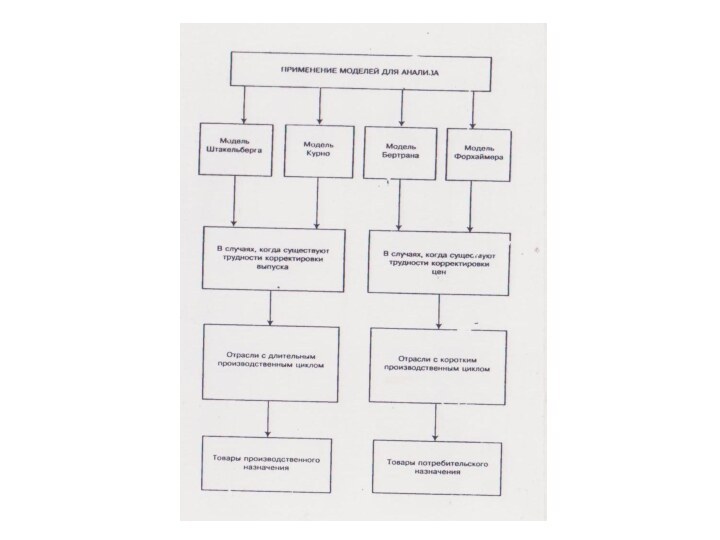
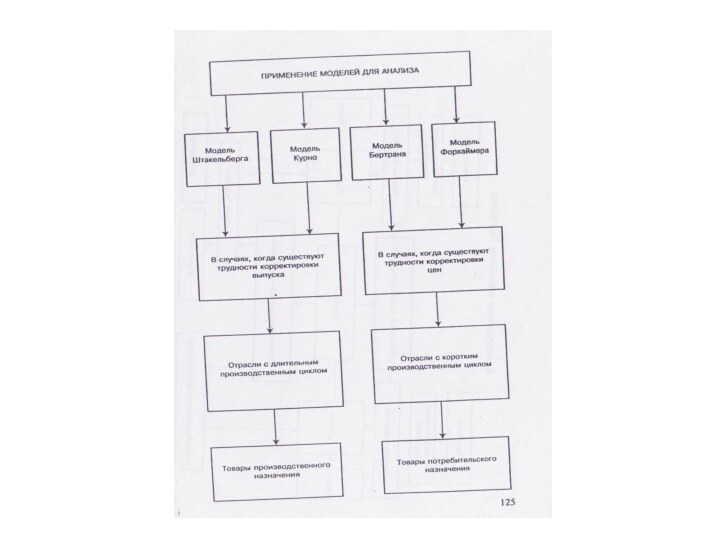
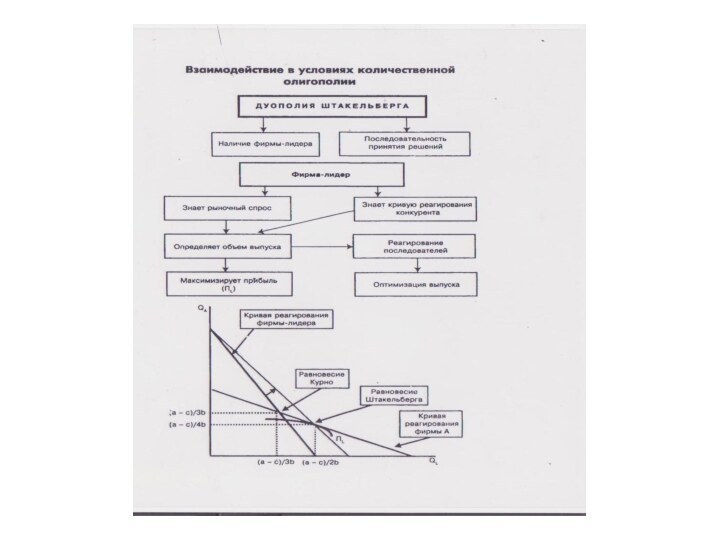
Модель олигополии Стэкльберга
Модель немецкого экономиста Генриха фон Стэкльберга
(1934 г) называют моделью лидерства по объему выпуска, или
моделью асимметричной дуополии. Модель Стэкльберга позволяет проанализировать взаимодействие фирм как лидеров и последователей.
Фирма считает себя лидером по объему выпуска, если ей удается первой принять решение об уровне выпуска. Лидер в модели Стэкльберга знает, что его соперник ведет себя по Курно, знает его функцию реакции и учитывает ее в собственной функции прибыли, которую он при этом максимизирует как монополист.
Последователь в модели Стэкльберга понимает, что конкурент является лидером, поэтому ведет себя так же, как и в модели Курно: максимизирует свою прибыль, считая выпуск соперника заданным ( рассматривает выпуск фирмы –лидера в качестве экзогенного параметра, т.е. принимает решение при нулевой предполагаемой вариации λ= ∂q1 / ∂q2=0).
Слайд 27
Модель Штакильберга
П1 = (a - bq1 -
bq2) q1– c q1, вместо q2 функцию реакции фирмы
2 (последователя) (6.23): q2 = -(1/2)q1+(а-с)/2b
тогда прибыль лидера :
П1L = [a – bqi – b((-1/2q1+(а-с)/2b] q1 – с q1 = aq1 – bqi 2 + b q12 /2- (а-с)/2b – с q1,
откуда П1L = ((а-с)/2) q1- bq12 / 2.
Условие первого порядка для максимизации прибыли фирмы 1-лидера :
∂ П1 / ∂q1 = ((a – c) / 2)- bq1 = 0
Отсюда находим:
q1L*= (a – c) / 2b.
Слайд 28
Модель Штакильберга
Равновесный выпуск фирмы - последователя 2 найдем,
подставив полученное значение выпуска лидера в уравнение функции реакции
фирмы 2 :
q2F* = - (a – c) / 4b + (a – c) / 2b = (a – c) / 4b
Равновесный отраслевой выпуск в дуополии Стэкльберга получим, просуммировав выпуск фирмы-лидера 1 и фирмы- последователя 2 :
Q*= q1 + q2 = 3(a – c) / 4b.
Равновесную цену получим, подставив значение отраслевого выпуска (6.52) в функцию рыночного спроса:
P* = a - b'3(a – c) / 4b = (a + 3c) / 4
Прибыль лидера составит:
П1= (а –с)2/8b
Прибыль последователя: П1= (а –с)2/16b
Вывод: преимущество первого хода позволяет фирме-лидеру получать прибыль в два раза большую, чем получит последователь. Поэтому последователь также хочет быть лидером
Слайд 29
Модель Штакильберга
2. Ситуация отраслевого равновесия по Стэкльбергу, если
фирма 2 будет выступать в роли лидера, а фирма
1 в роли последователя представлена точкой S2L . Поскольку мы исходили из симметричных функций спроса и издержек, то результаты для ситуации, когда фирма 2 станет лидером, а фирма 1 последователем , будут такими же, что и в случае лидерства фирмы 1 и последователя фирмы 2 с той только разницей, что индексы в формулах будут изменены с q1 на q2.
3) В ситуации, когда обе фирмы претендуют на роль лидера, отраслевое равновесие в модели Стэкльберга не достигается. Тогда во избежании "ценовой войны" дуополисты должны будут договориться: либо о том, что кто из них все же станет лидером, либо создадут картель, который позволит максимизировать прибыль отрасли.
Слайд 30
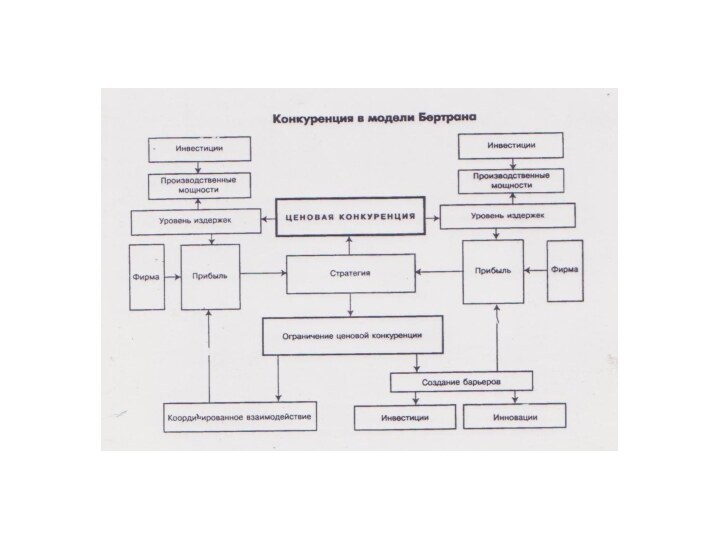
Модель олигополии Бертрана
Французский математик Жозеф Бертран ( 1883
г. ) в качестве альтернативы дуополии Курно предложил свою
модель дуополии.
Он исходил из тех же предпосылок, которые сделал Курно (отсутствие сговора, однократность взаимодействия, однородность продукта, наличие неизменных и равных предельных издержек у фирм, закрытый вход).
Но в качестве стратегической переменной выступает цена, а не объем выпуска. Причем цену определяет каждый из дуополистов Бертрана, считая выбор соперника неизменным.
Пусть в отрасли действуют всего 2 фирмы, производится однородный продукт с одинаковыми и неизменными предельными издержками.
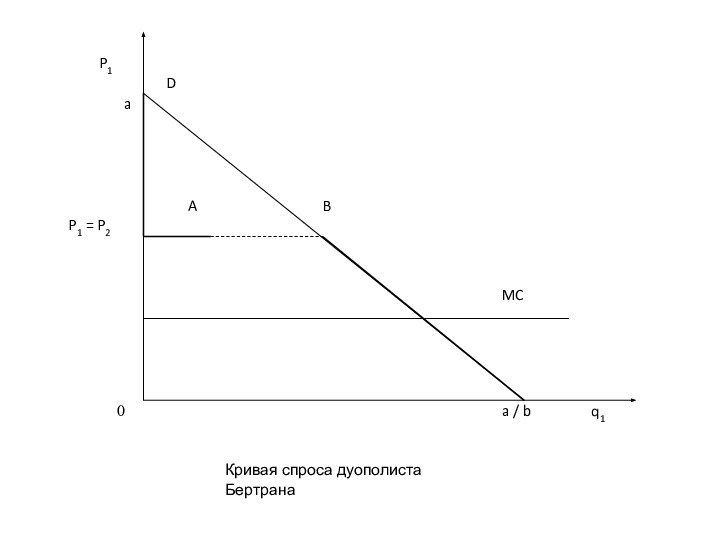
Предположим для простоты, что функция спроса - линейна:
Q = q1 + q2 = a / b – 1 / bP)
Кривая спроса дуополиста Бертрана
P1 = P2
В этом случае спрос на продукцию каждой из фирм зависит от цен на товар. Если цена, назначенная фирмой 1, превысит цену, назначенную фирмой 2, то никто не захочет покупать продукцию у фирмы 1.
Слайд 33
Кривая спроса дуополиста Бертрана
Слайд 34
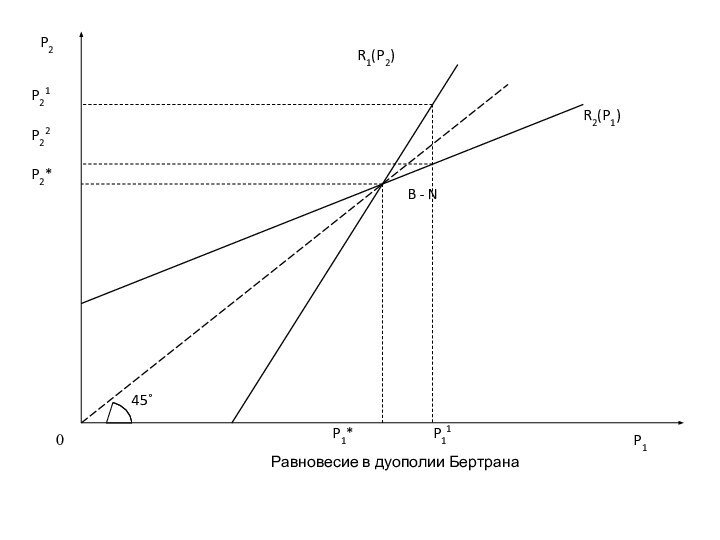
Модель Бертрана
Таким образом, кривая спроса на продукцию фирмы
1 состоит из трех отрезков):
d1(Р1, Р2) = 0, если
Р1 > Р2 (отрезок аР2 )
d1(Р1, Р2) = D(p1)/2, если Р1 = Р2 (т. А )
d1(Р1, Р2) = D(p1), если Р1 < Р2 (отрезок Bb ).
Также будет выглядеть и функция спроса для фирмы 2.
Каждой фирме выгодно назначить цену чуть-чуть ниже конкурента. Тогда фирма, снизившая цену первой, сможет захватить весь рынок, поскольку продукция однородная, а потребители ведут себя рационально и выбирают при прочих равных тот товар, который дешевле. Предполагая (в соответствии с допущениями модели), что объявленные соперником цены неизменны, эта фирма фактически становится монополистом, захватывает весь рынок
Слайд 36
Модель Бертрана
модель Бертрана является моделью "ценовой войны"

в дуополии. Равновесие будет достигнуто лишь при снижении рыночной
цены до уровня предельных издержек. Поскольку МС=соnst, то МС=АС (предельные издержки равны средним).
Результатом ценовой войны (при соблюдении всех вышеназванных предпосылок) становится объем производства, который производился бы и в условиях рынка совершенной конкуренции.
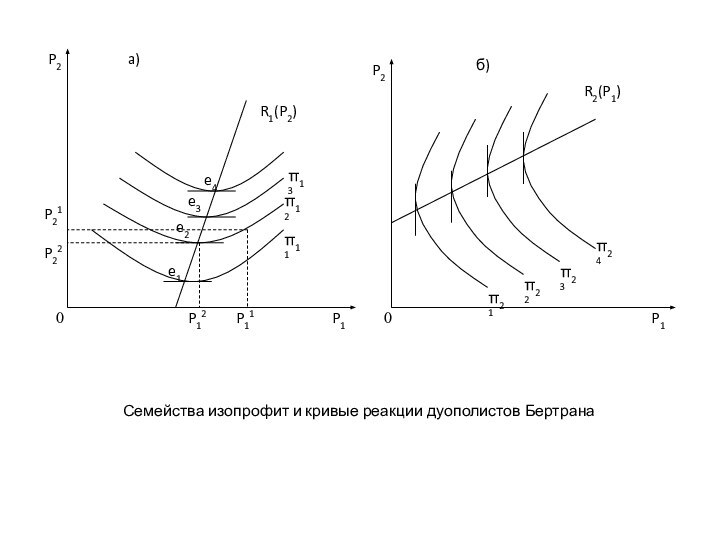
Изопрофиты у дуополистов Бертрана строятся в осях назначаемых фирмами цен (P1, P2) и являются не вогнутыми (как в дуополии Курно), а выпуклыми к соответствующим осям. Такая форма изопрофит объясняет необходимость снижения цены каждым из дуополистов в ответ на снижение цены соперника, для сохранения уровень прибыли неизменным.
Если фирма 2 снизит цену с P2 1 до с P2 2,то фирма 1 должна снизить цену с P1 1 до P12, для сохранения на неизменном уровне прибыли П12.
Если конкурент и дальше будет уменьшать цену, фирма 1 получит меньшую прибыль П11, представленную более низкой изопрофитой (.
При такой форме изопрофит существует единственная цена для фирмы 1, которая, при существующей цене фирмы 2, дает максимум прибыли для фирмы 1 (
Кривые реакции фирм строятся путем соединения самых низких точек изопрофит . Кривые реакции представляют собой геометрическое место точек, соединяющих максимумы прибыли, которую получает каждая из фирм при назначении оптимальной цены (которая дает максимум прибыли) при заданном уровне цены конкурента.
Слайд 37
Модель Бертрана
Пусть функция спроса на продукцию дуополиста Бертрана
имеет вид:
d(Pi, Pj)=ai-bi Pi+ кPj, где i,j =
1, 2, i ≠ j и аi, bi, к > 0.
Предельные издержки составляют сi, причем (с1 = с2).
Для того, чтобы вывести функцию реакции для дуополиста Бертрана, запишем его функцию прибыли:
Пi = (Pi - Ci)( ai - bi Pi + кPj) = Pi ai - Ci ai - bi Pi2 + Ci bi Pi + кPj Pi - Ci кPj)
Необходимое условие максимизации прибыли:
∂ Пi / ∂Pi = ai – 2biPi + Ci bi + кPj= 0,
отсюда функция реакции дуополиста Бертрана RFi.:
Pi = (ai + Ci bi ) / 2 bi + (к / 2 bi) P2 = Ai +BiPj где
Ai = (ai + Ci bi ) / 2 bi , . Bi=(к / 2 bi)
Функции реакции дуополистов Бертрана – линейны (т.к.. ∂ Pi / ∂Pj = 0 ), имеют положительный наклон и пересекаются в точке равновесия Бертрана –Нэша, точке B-N с координатами ( РВ1, РВ2 ),
при РВ1 = (Ai + Aj Bi) / (1 - Bi Bj).
Слайд 40
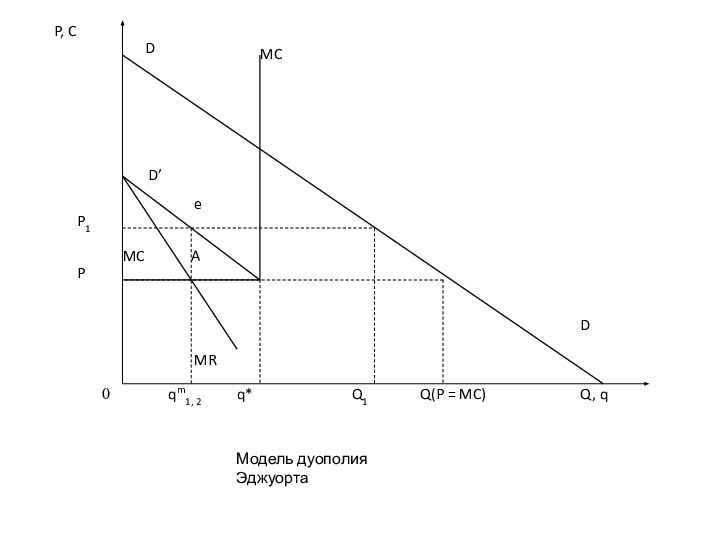
Модель Эджуорта
Пусть возможности производства на каждом предприятии ограничены

половиной рыночного спроса при цене, равной предельным затратам,
qm1,2
= Q(P = МС)/2.
Если каждая фирма установит начальную цену на уровне P1=Р2=МС, то их совместный выпуск окажется как раз таким, что будет в состоянии обеспечить совокупный рыночный спрос, Q(P = МС).
Если фирма-дуополист 1 хотя бы чуть-чуть повысит свою цену, а дуополист 2 оставит цену неизменной на уровне предельных издержек, Р2 = МС, то все покупатели перейдут к нему из-за более низкой цены.
Но тут фирма-дуополист 2 сталкнется с ограничением по размеру производственной мощности. Они у него таковы, что он не может удовлетворить больше половины рыночного спроса, поскольку именно такова его производственная мощность. В итоге не всем покупателям достанется продукция по пониженной цене, и им придется покупать продукцию у фирмы-дуополиста 1.
Получив для себя остаточный спрос в размере (Q(P = МС) - q*), фирма-дуополист 1 сможет максимизировать свою прибыль, действуя как монополист в отношении этого остаточного спроса. В точке А предельные издержки равны предельной выручке, поэтому с целью максимизации прибыли дуополист 1 установит цену Р1, при которой объем производства составит:
ql = Q(P = MC)/4.
Слайд 42
Модель Эджуорта
В ответ на это дуополист 2 повысит
свою цену до уровня несколько меньшего, чем цена Р1,
для того, чтобы переманить к себе его покупателей. Но в связи с ограниченностью своих производственных мощностей дуополист 2 сможет насытить спрос лишь в объеме:
Q1- ql = 2/3 Ql =Q1(P = МС)/2
Реализуя вдвое больше продукции по цене, по немногим меньшей, чем у фирмы-дуополиста 1, фирма-дуополист 2 будет иметь и вдвое большую прибыль.
Поэтому фирма-дуополист 1 в свою очередь снизит цену до уровня чуть ниже, чем цена дуополиста 2.
Так они будут стремиться опередить друг друга в снижении цен. Желание получить большую прибыль от снижения цены будут продолжаться, пока цена не достигнет уровня:
Р=МС+(Р1-МС)q1/q2
Слайд 43
Модель Эджуорта
если фирма 1 снизит свою цену до
Р, т.е. сделает ее немногим меньше цены конкурента, она
сможет реализовать максимально возможный нее объем выпуска q*.
Если фирма 1 увеличит свою цену до Р1, она сможет продать лишь q1 единиц продукции. Поэтому фирма 1, чтобы получить прибыль, такую же, как и при цене Р1 назначит цену
Р=МС+(Р1-МС)q1/q2.
Но как только цена станет равной Р, выгодным для любой фирмы-дуополиста снова станет повышение цены до Р1, и весь ценовой цикл повторится.
Итак, модель Эджуорта не позволяет достигнуть статичного равновесия. Это своего рода «ценовая ловушка», оказавшись в которой дуополисты втягиваются в нескончаемую ценовую войну, в которой снижение цен сменяется их повышением.
Слайд 44
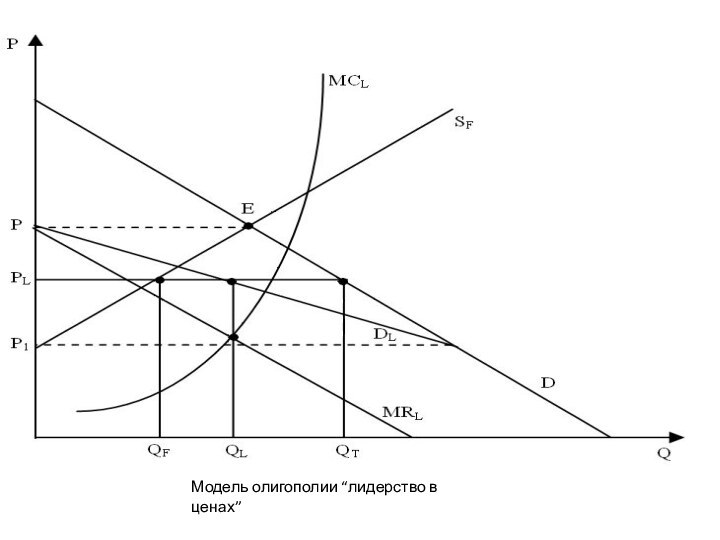
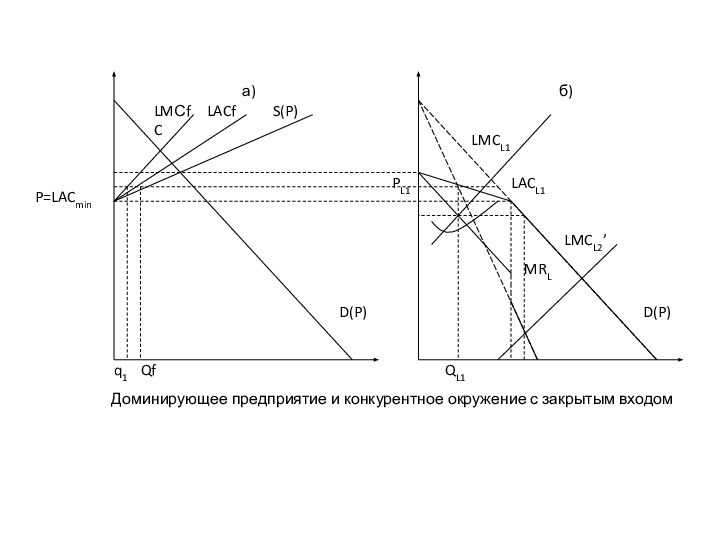
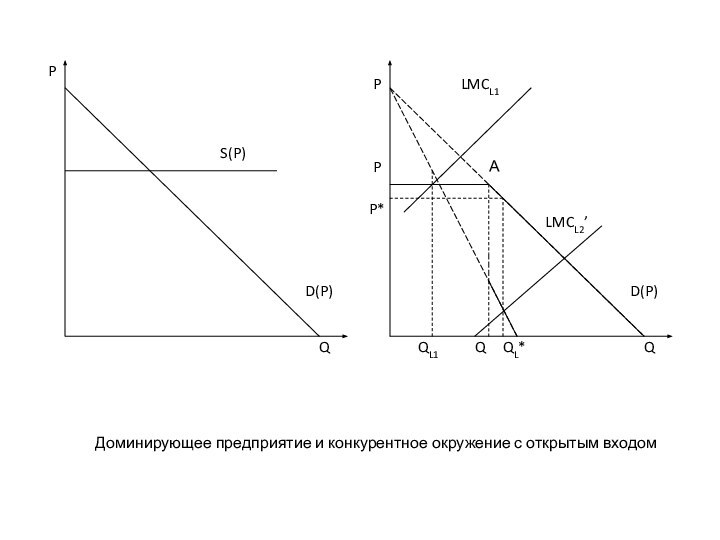
“Лидер” и конкурентное окружение
Слайд 45
Модель олигополии “лидерство в ценах”
Слайд 49
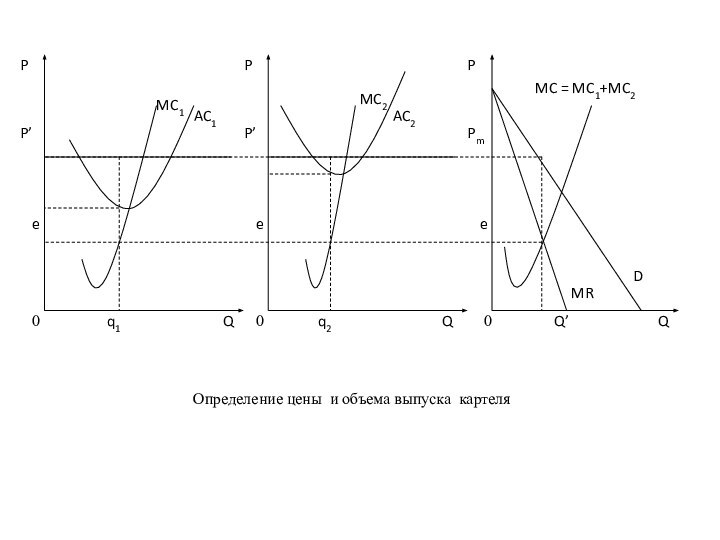
Картель
Картель максимизирует свою прибыль
: П Мах =
П1 + П2
при Рm =f(Q) = f(q1 +
q2) ,
: ТС1 = f 1(q1 ),ТС2 = f 2(q2 ), то поскольку прибыль 1 фирмы П1 = TR1 - ТС1
и прибыль второй фирмы П2 = TR2 - ТС2,,
то совокупная прибыль П= TR1+ TR2 – TС1 - TС2 = TR- TС1 - TС2.
Поскольку каждая добавочная единица выпуска должна приносить одинаковый доход, независимо от того, какая из фирм-членов картеля ее произвела, то предельная выручка отрасли равна:
∂TR /∂Q=∂TR / ∂q1 = ∂TR /∂ q2
(Условия максимизации прибыли первого и второго порядка находятся как и в случае монополиста с несколькими заводами .
Слайд 50
Стратегияи курка, .
Допущения:
Фирмы-участники сговора ежедневно устанавливают цену
РС до тех пор, пока никто не подрывает соглашения.
В случае обмана наказание будет состоять в том, что участники соглашения (включая обманщика) устанавливают цену на уровне предельных издержек.
Если обе фирмы честно устанавливают РС, то они делят между собой рыночные продажи в объеме D(РC) поровну, и дневная прибыль каждой из фирм составляет : ПС = 0,5 (PC - c)• D(PC) = ПМ / 2.
Какую прибыль получит обманщик (пусть им будет фирма 1) до момента разоблачения? Из анализа дуополии Бертрана известно, что если фирма 2 (фирма, выполняющая соглашение) установит Р2 = PC, то фирме 1 достаточно будет лишь назначить свою цену лишь немногим меньше этой цены, чтобы
захватить весь рынок, получив при этом:
ПС = D(PC — ε) • (РС — ε — с) = 2ПС = ПМ,
где ε — бесконечно малая величина.
Слайд 51
Стратегияи курка (наказания)
Обман позволяет фирме 1 увеличить получаемую

прибыль в два раза. ПН при данной стратегии равна
нулю.
Поскольку одна из фирм ежедневно устанавливает цену на уровне предельных издержек, то в интересах другой фирмы поступать таким же образом;.
Подсчитаем теперь выгоды и потери от обмана при дневной ставке процента i, в зависимости от того, сколько дней уйдет на отслеживание обмана.
Пусть на это уйдет всего 1 день. При Т = 1 выгоды от обмана составят
П0 - ПC = 2 ПC - ПC = ПC = ПМ / 2
Потери от обмана равны текущей стоимости, которая теряется из-за того, что обман раскрыт и последовало наказание.
Прибыль, которую потеряет нарушитель составит: ПМ / 2., поскольку он мог получить за день ПC = ПМ / 2, а получит только П = 0. А так как нулевую прибыль он будет получать с момента обнаружения обмана бесконечно долго, то согласно формуле дисконтирования для бесконечного потока доходов, цена наказания, выраженная в потерянной прибыли будет равна:
ПC / (1 + i) + ПC / (1 + i)2 + … = ПC / I (6.69)
Слайд 52
Стратегия наказания
При нулевом лаге отслеживания, при Т =

1 устойчивость соглашения высока. Чтобы была заинтересованность в нарушении
соглашения должно выполняться неравенство: ПC > ПC / I, но это предполагает значение i = 100%. Значит, если дневная норма процента i будет меньше 100%, нарушение соглашения не произойдет.
Поддержание соглашения, прежде всего, зависит от временного лага раскрытия обмана.
Пусть на установление факта нарушения соглашения затрачено два дня, т.е. Т = 2.
Поскольку безнаказанный обман длится 2 дня текущая стоимость выгод от обмана составит:
ПC + ПC / (1 + i) = ПC(2 + i) / (1 + i)
a текущая стоимость потерь от обмана составит:
ПC / (1 + i)2 + ПC / (1 + i)3 + … ПC / (1 + i)n = ПC / i(1 + i)
с увеличением возможности скрыть обман, издержки обмана уменьшаются, а выгоды от него возрастают.
Неравенство ПC(2 + i) / (1 + i) > ПC / i(1 + i) обращается в равенство при i ≈ 0,41, и, стало быть, соблюдается при значениях нормы процента ниже 41%. Это — все еще достаточно высокие значения нормы процента, но уже гораздо более реальные, чем 100%. Таким образом, при 2-дневном лаге отслеживания обмана фирма-участник сговора пойдет на обман, если дневная норма процента будет ниже 41%.