- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Операции наращения и дисконтирования
Содержание
- 2. Темп прироста
- 3. Темп снижения
- 4. Взаимосвязь показателей
- 5. Формула наращения или
- 6. Формула дисконтирования
- 7. Понятие простого и сложного процента.
- 8. Схема простых процентов (simple interest):Сумма, получаемая к возврату через n периодов
- 9. Схема сложных процентов (compound interest):размер инвестрованного капитала будет равен:к концу первого года
- 10. к концу второго года:
- 11. к концу n-го года: или
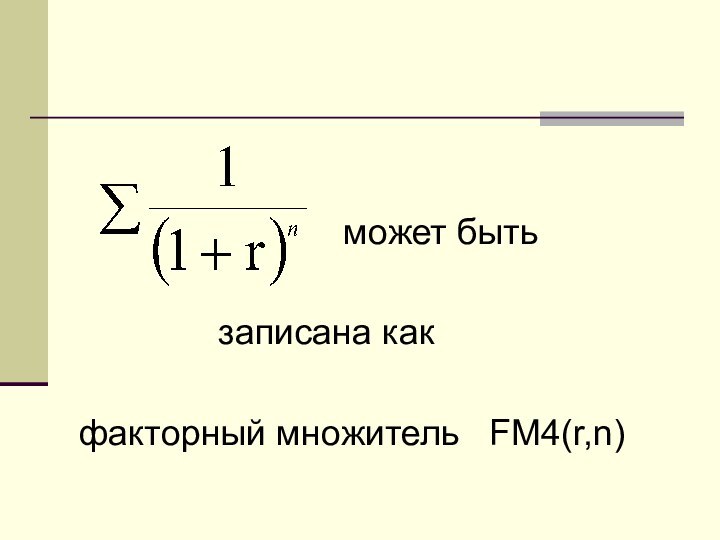
- 12. факторный множитель
- 13. Внутригодовые процентные начисления.
- 14. Вложено в банк 5млн у.е. под 10% на два года, с полугодовым начислением
- 15. Если пользоваться формулой, то m = 2, n = 2
- 16. Эффективная годовая процентная ставка.В рамках одного года
- 17. Из определения эффективной годовой процентной ставки следует, что
- 18. Отсюда
- 19. Пример:Предприниматель может получить ссуду а) на условиях
- 20. а)б)
- 21. Оценка приведенной стоимости.Базовая расчетная формула
- 22. Оценка денежных потоков.может осуществляться в рамках решения
- 23. Прямая задача предполагает суммарную оценку наращенного денежного потока, т.е. в его основе лежит будущая стоимость.
- 24. Обратная задача предполагает суммарную оценку дисконтированного (приведенного) денежного потока.
- 25. Денежный поток с неравными поступлениями.с позиции будущего (прямая задача)или
- 26. C позиции текущего момента (обратная задача)
- 27. дисконтирующий множитель тогда
- 28. Пример:
- 29. Срочный аннуитет.Срочным аннуитетом называется денежный поток с равными поступлениями в течение ограниченного промежутка времени.
- 30. Схема постнумерандо (ordinary annuity)Означает, что начисление
- 31. Прямая задача (постнумерандо)
- 32. Тогда формула приобретает следующий вид.
- 33. Прямая задача пренумерандо
- 34. Обратная задача оценки срочного аннуитета
- 36. Тогда формула приобретает следующий вид
- 37. Бессрочный аннуитет.денежные поступления продолжаются достаточно длительное время
- 38. Бессрочный аннуитет обратная задача
- 39. Методы оценки эффективности инвестиционных проектовМетоды, основанные на учетных оценкахМетоды, основанные на дисконтированных оценках
- 40. Методы, основанные на учетных оценкахРасчет срока окупаемости инвестицииРасчет коэффициента эффективности инвестиции
- 41. Метод определения срока окупаемости инвестицийPay back
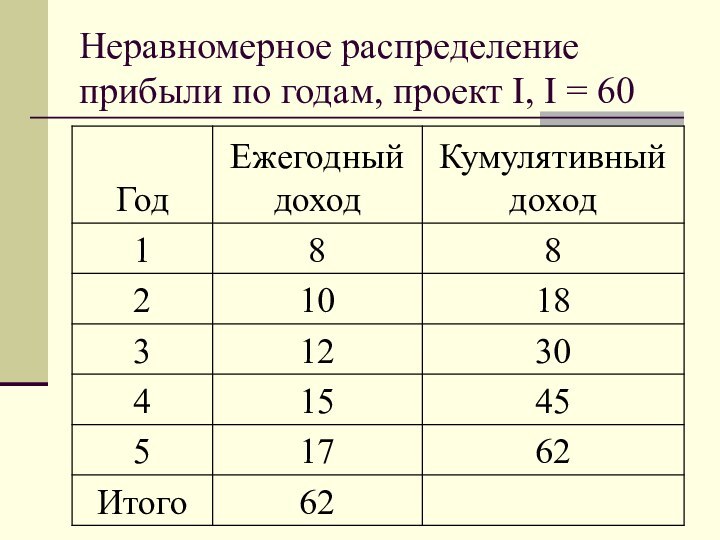
- 42. Неравномерное распределение прибыли по годам, проект I, I = 60
- 43. Неравномерное распределение прибыли по годам, проект II, I = 60
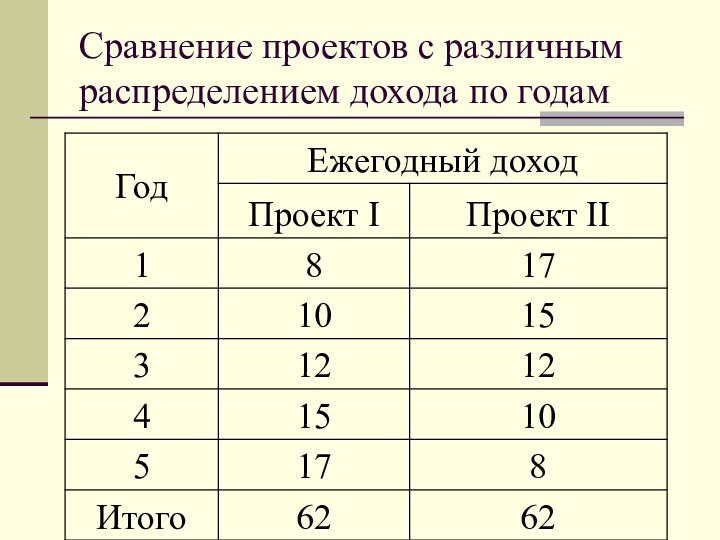
- 44. Сравнение проектов с различным распределением дохода по годам
- 45. Коэффициент эффективности инвестиций Benefit-cost ratio
- 46. Методы, основанные на дисконтированных оценкахРасчет чистого приведенного эффектаРасчет индекса рентабельности инвестицииРасчет внутренней нормы рентабельности инвестиции
- 47. Чистый приведенный эффект Net present value
- 48. Индекс рентабельности инвестиций Present value index
- 49. Скачать презентацию
- 50. Похожие презентации
Темп прироста



















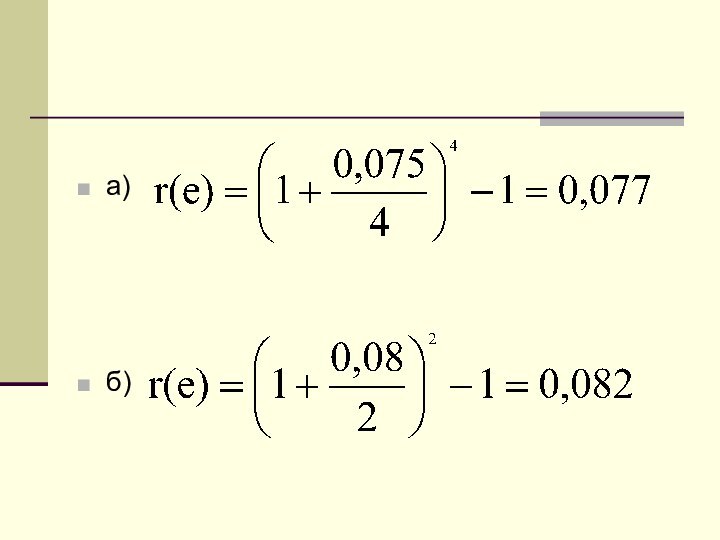

























Слайд 9
Схема сложных процентов (compound interest):
размер инвестрованного капитала будет
равен:
к концу первого года
Слайд 19
Пример:
Предприниматель может получить ссуду
а) на условиях ежеквартального
начисления процентов из расчета 7,5% годовых;
б) или на
условиях полугодового начисления процентов из расчета 8% годовых. Какой вариант предпочтительней?
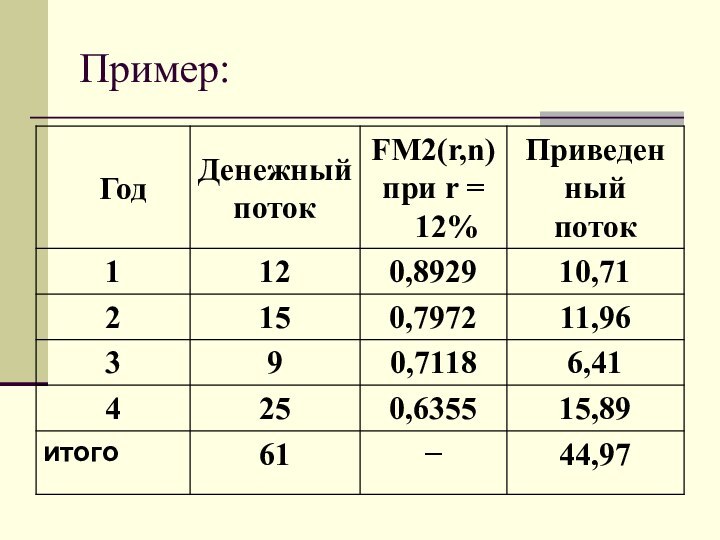
Слайд 22
Оценка денежных потоков.
может осуществляться в рамках решения двух
задач:
прямой, т.е. проводится оценка с позиции будущего (реализуется схема
наращения);обратной, т.е. проводится оценка с позиции настоящего (реализуется схема дисконтирования).