- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Принятие решений как особый вид человеческой деятельности
Содержание
- 2. Введениепринятие решений как особый вид человеческой деятельностиальтернативыкритерииоценка важности критериев
- 3. Принятие решений как особый вид человеческой
- 4. АльтернативыАльтернатива – это один из возможных способов
- 5. Классификация альтернатив
- 6. КритерииВарианты решений (альтернативы) характеризуются различными показателями их
- 7. Полнота и действенность критериевПолнота набора означает, что
- 8. Разложимость, неизбыточность, минимальность критериевРазложимость. При использовании n
- 9. Оценка важности критериевМетоды определения оценки значимости критерия
- 10. Тема 1. Анализ задач и методов
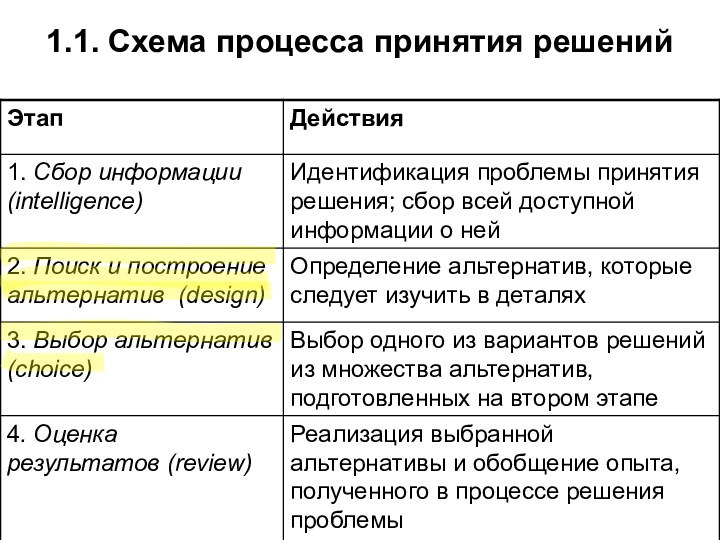
- 11. 1.1. Схема процесса принятия решений
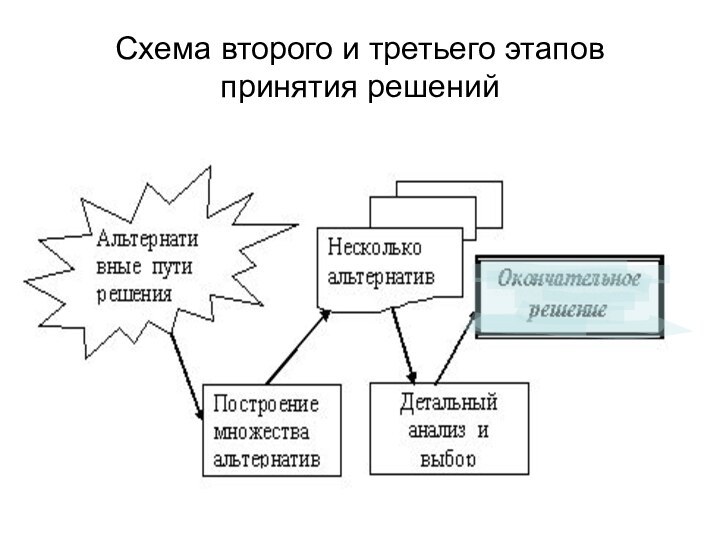
- 12. Схема второго и третьего этапов принятия решений
- 13. 1.2. Классификация задач принятия решенийЗадачу
- 14. Традиционные классификации задач принятия решений1. По виду
- 15. Задачи принятия решений в условиях определённостиК этому
- 16. Основные условия применимости методов
- 17. Задачи принятия решений в условиях рискаВ тех
- 18. Задачи принятия решений в условиях неопределённостиЭти задачи
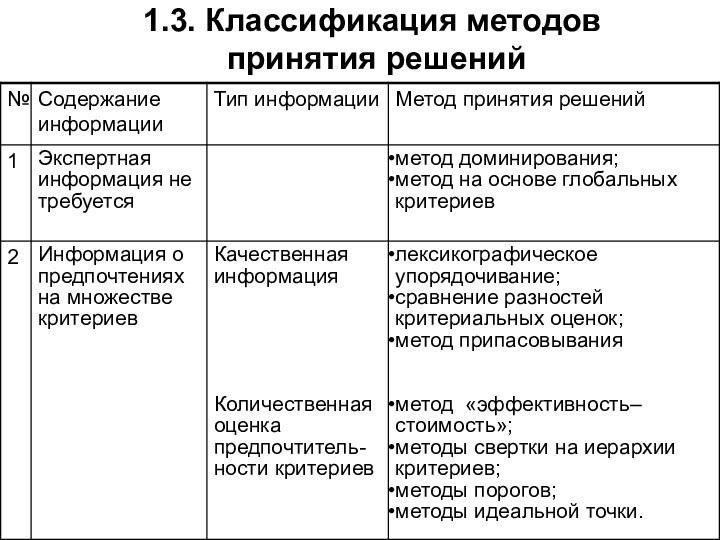
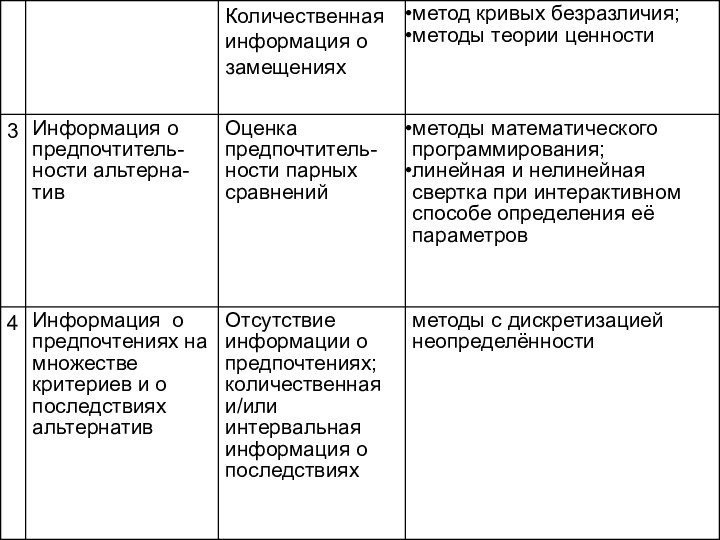
- 19. 1.3. Классификация методов принятия решений
- 22. 1.4. Системы поддержки принятия решений Термин «система
- 23. Процедура принятия решений с помощью систем поддержкиВсе
- 24. Скачать презентацию
- 25. Похожие презентации
Введениепринятие решений как особый вид человеческой деятельностиальтернативыкритерииоценка важности критериев




















Слайд 2
Введение
принятие решений как особый вид
человеческой деятельности
альтернативы
критерии
оценка важности
критериев
Слайд 3
Принятие решений как особый вид
человеческой деятельности
Принятие решения
в большинстве случаев возможных альтернатив решений, их оценке и
выборе лучшей.Что же такое «наилучшее» решение? В исследованиях операций «наилучшим» считается решение доставляющее оптимум функции, выражающей цель системы. Более общее определение «правильного» или «наилучшего» решения в смысле принятия считают выбор такой альтернативы из числа возможных, в которой с учетом всех разнообразных факторов и противоречивых требований будет оптимизирована общая ценность, то есть она будет в максимальной степени соответствовать достижению поставленной цели. Отметим, что в отличии от исследования операций, в теории принятия решений не существует абсолютно лучшего решения. Решения является лучшим лишь для конкретного лица принимающего решение, в отношении поставленных им целей, при заданных условиях. Эта субъективная оценка оказывается в настоящее время единственно возможной основой объединения разнородных физических параметров решаемой проблемы в единую модель, позволяющую оценивать варианты решений. судить исходя только из своих субъективных предпочтений.
Слайд 4
Альтернативы
Альтернатива – это один из возможных способов достижения
цели или один из конечных вариантов решений.
Альтернативы отличаются
друг от друга последовательностью и приемами использования активных
ресурсов. Для любой задачи принятия решений должна
существовать тройка: цель, критерии, альтернативы.
Если отсутствует один из компонентов, то проблема не
поставлена. При наличии менее двух альтернатив,
отсутствует выбор.
Задача формирования исходного множества альтернатив –
составная часть процесса принятия решений. Даже если
выбор ограничен плохими, очень плохими и абсолютно
неудовлетворительными альтернативами, - всегда
существует наиболее благоприятное решение.
Слайд 6
Критерии
Варианты решений (альтернативы) характеризуются
различными показателями их привлекательности
для ЛПР.
Эти показатели называют критериями.
В профессиональной деятельности выбор
критериев часто определяется многолетней практикой, опытом. В
подавляющем большинстве задач выбора имеется
достаточно много критериев оценок вариантов решений.
Существует ряд свойств или требований, которым должен (по
возможности) удовлетворять набор критериев. Набор
критериев должен быть:
полным,
действенным,
разложимым,
неизбыточным,
минимальным.
Слайд 7
Полнота и действенность критериев
Полнота набора означает, что он
должен охватывать все важные аспекты проблемы. Набор критериев является
полным, если с его помощью можно показать степень достижения общей цели, то есть набор из критериев полон, если зная значения n-мерного критерия, связанного с общей целью, ЛПР имеет полное представление о степени достижения общей цели.Действенность критериев. ЛПР должен понимать смысл критериев и влияние их действий на обсуждаемую проблему. Критерии должны быть такими, чтобы их можно было объяснять другим, особенно в тех случаях, когда важнейшей целью работы является выработка и защита определенной позиции. Поскольку смысл анализа решений помочь ЛПР выбрать лучший курс действий, то и критерии должны служить этой цели.
Слайд 8
Разложимость, неизбыточность, минимальность критериев
Разложимость. При использовании n критериев
необходимо построить n-мерную функцию предпочтений. Для задач с большим
числом критериев полезно произвести декомпозицию задачи и разложить ее на подзадачи, каждая из которых содержит меньшее число критериев. То есть желательно, чтобы набор критериев был разложим.Неизбыточность. Критерии должны быть определены так, чтобы не дублировался учёт одних и тех же аспектов решаемой проблемы.
Минимальная размерность. Желательно, чтобы набор критериев оставался настолько малым, насколько это возможно. Увеличение числа критериев приводит, с одной стороны, к анализу решаемой задачи в более широком плане, с другой стороны, может сильно усложнить и запутать анализ, что приведет к ошибочности результатов.
Слайд 9
Оценка важности критериев
Методы определения оценки значимости критерия («весов»
приоритетов) подразделяют на 3 категории.
Используются опыт и знания
ЛПР. Составляется список критериев, и ЛПР вычеркивает из списка критерии которые с
его точки зрения не имеют большого значения. При
отсутствии в списке необходимых критериев, ЛПР может его
дополнить. Определение «веса» каждого критерия не
формализуется.
Значимость критериев определяется на основе оценок
текущего и желательного состояния объекта по каждому
критерию, опыта и знаний.
Значимость критериев определяется на основе оценок
текущего и желательного состояние объекта по каждому
критерию, динамики объекта при нулевых управляющих
воздействиях по каждому критерию, опыта и знаний.
Слайд 10 Тема 1. Анализ задач и методов оптимальных решений
схема процесса принятия решений
классификация задач принятия решений
классификация методов принятия
решенийсистемы поддержки принятия решений
Слайд 13
1.2. Классификация задач
принятия решений
Задачу принятия решений
можно представить
следующим набором информации:
(T, A, K, X,
F, G, D), T – постановка задачи (например, выбрать лучшую
альтернативу или упорядочить весь набор);
A – множество допустимых альтернативных вариантов;
K – множество критериев выбора;
Х – множество методов измерения предпочтений (например,
использование различных шкал);
F – отображение множества допустимых альтернатив в
множество критериальных оценок (исходы);
G – система предпочтений эксперта;
D – решающее правило, отражающее систему предпочтений.
Любой из элементов этого набора может служить
классификационным признаком принятия решения.
Слайд 14
Традиционные классификации задач принятия решений
1. По виду отображения
F.
Отображение множества А и К может иметь
детерминированный характер,
вероятностный или неопределённый вид, в соответствии с которым задачи
принятия решений можно разделить на задачи в условиях
риска и задачи в условиях неопределённости.
2. По мощности множества К.
Множество критериев выбора может содержать один элемент
или несколько. В соответствии с этим задачи принятия
решений можно разделить на задачи со скалярным критерием
и задачи с векторным критерием (многокритериальное
принятие решений).
3. По типу системы G.
Предпочтения могут формироваться одним лицом или
коллективом, поэтому задачи принятия решений можно
классифицировать на задачи индивидуального принятия
решений и задачи коллективного принятия решений.
Слайд 15
Задачи принятия решений в условиях определённости
К этому классу
относятся задачи, для решения
которых имеется достаточная и достоверная
количественная
информация. В этом случае применяются методы
математического программирования, суть которых
состоит в нахождении оптимальных решений на базе
математической модели реального объекта.
Слайд 16 Основные условия применимости методов математического
программирования
Задача должна быть хорошо формализована, т. е.
имеется адекватная
математическая модель реального объекта.
2. Существует некоторая целевая функция (критерий
оптимизации), позволяющая судить о качестве
рассматриваемых альтернативных вариантов.
3. Имеется возможность количественной оценки
значений целевой функции.
4. Задача имеет определенные степени свободы
(ресурсы оптимизации), т. е. некоторые параметры
Функционирования системы, которые можно изменять в
некоторых пределах в целях улучшения значений
целевой функции.
Слайд 17
Задачи принятия решений в условиях риска
В тех случаях,
когда возможные исходы можно описать с
помощью некоторого вероятностного
распределения, имеют место задачи принятия решений в условиях риска.
Для построения распределения вероятностей необходимо
либо иметь в распоряжении статистические данные, либо
привлекать знания экспертов. Обычно для решения задач
этого типа применяются методы теории одномерной или
многомерной полезности. Эти задачи занимают место на
границе между задачами принятия решений в условиях
определенности и неопределенности.
Для решения этих задач привлекается вся доступная
информация (количественная и качественная).
Слайд 18
Задачи принятия решений в условиях неопределённости
Эти задачи имеют
место тогда, когда информация,
необходимая для принятия решений, является
неточной, неполной, неколичественной, а формальные модели
исследуемой системы либо слишком сложны, либо
отсутствуют. В таких случаях для решения задачи обычно
привлекаются знания экспертов.
Слайд 22
1.4. Системы поддержки принятия решений
Термин «система поддержки
принятия решений» появился в
начале 70-х годов, и за это
время было дано большое число определений этого понятия:
1. Системы поддержки принятия решений являются человеко-машинными объектами, которые позволяют лицам, принимающим решения, использовать данные, знания, объективные и субъективные модели для анализа и решения слабоструктурированных и неструктурированных проблем.
2. Система поддержки принятия решений – это компьютерная система, позволяющая ЛПР сочетать собственные субъективные предпочтения с компьютерным анализом ситуации при выборе рекомендаций в процессе принятия решения.
3. Система поддержки принятия решений – компьютерная информационная система, используемая для различных видов деятельности при принятии решений в ситуациях, где невозможно или нежелательно иметь автоматическую систему, полностью выполняющую весь процесс.
Слайд 23
Процедура принятия решений с помощью
систем поддержки
Все три определения
не противоречат, а дополняют друг
друга и достаточно полно
характеризуют систему поддержки принятия решений.
Человеко-машинная процедура принятия решений с помощью
систем поддержки представляет собой циклический процесс
взаимодействия человека и компьютера.
Цикл состоит из
фазы анализа и постановки задачи для компьютера,
выполняемой ЛПР, и
фазы оптимизации (поиска решения), реализуемой
компьютером.





























