- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Вероятностные модели управления запасами
Содержание
- 2. Введем следующие обозначения. ▪
- 3. На рис. 1 показана зависимость между размером
- 4. Вероятностное условие, которое определяет размер резервного запаса
- 5. Величина спроса на протяжении срока выполнения заказа
- 6. В новой модели допускается неудовлетворенный спрос (рис.
- 7. В рассматриваемой модели приняты три допущения.
- 8. Основываясь на этих определениях, вычислим компоненты функции
- 9. 3. Ожидаемые потери, связанные с неудовлетворенным спросом.
- 10. Оптимальные значения у* и R* определяются из
- 11. При R = 0 последние два уравнения
- 12. 2. Одноэтапные модели Одноэтапные модели управления
- 13. 2.1. Модель при отсутствии затрат на оформление
- 14. Ожидаемые затраты М{С(у)} на период выражаются следующей
- 15. Ранее предполагалось, что спрос D является непрерывной
- 16. 2.2. Модель при наличии затрат на оформление
- 17. Так как К является константой, минимум величины
- 18. Задача формулируется следующим образом. Какое количество продукции
- 19. Случай 2 (s≤x≤S). Из рис. 5 видно,
- 20. 3. Многоэтапные модели Рассматривается многоэтапная модель
- 21. Используя обозначения из раздела 2 и предполагая,
- 22. Задачу можно решить рекуррентно методами динамического программирования.
- 23. Величина определяется следующим образом. Если на
- 24. 4. Заключение В моделях управления запасами спрос
- 25. Основные соотношения СМО В теории МО обычно рассматривается
- 26. Рассмотрим
- 27. Модель Эрланга Допущения:
- 28. Перенесем Pn(t) в левую часть
- 29. Приравняв к нулю производные в (3), получим:
- 30. Математическое ожидание (L) числа требований, находящихся в
- 31. Формула Поллачека-Хинчина
- 32. Скачать презентацию
- 33. Похожие презентации
Введем следующие обозначения. ▪ L — срок выполнения заказа, т.е. время от момента размещения заказа до его поставки; ▪ X1— случайная величина, представляющая величину спроса на протяжении срока выполнения заказа;



























![Вероятностные модели управления запасами Возьмем мат. ожидание от этих величин E[q/] = E[q] – E[1] +](/img/tmb/12/1153803/6aac590b0d59c5db8efa7222d1b466b8-720x.jpg)
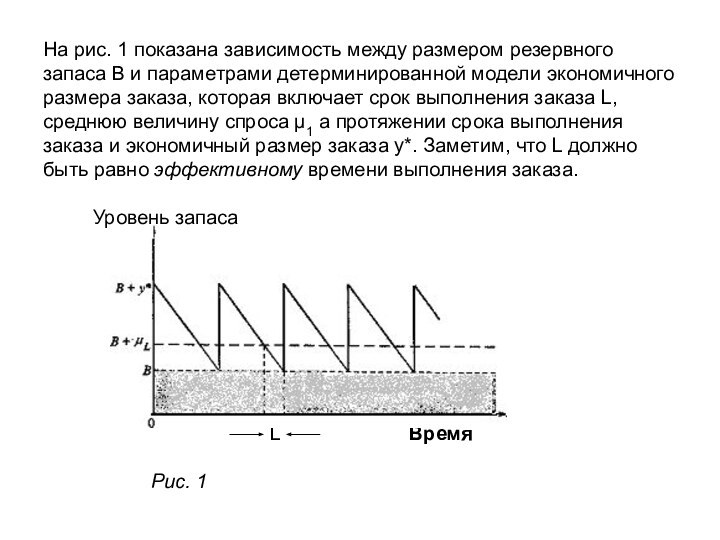
Слайд 3 На рис. 1 показана зависимость между размером резервного
запаса В и параметрами детерминированной модели экономичного размера заказа,
которая включает срок выполнения заказа L, среднюю величину спроса μ1 а протяжении срока выполнения заказа и экономичный размер заказа у*. Заметим, что L должно быть равно эффективному времени выполнения заказа. Уровень запаса L Время Рис. 1Слайд 4 Вероятностное условие, которое определяет размер резервного запаса В,
имеет вид: По определению случайная величина является нормированной нормально распределенной случайной
величиной, т.е. имеет распределение N(0, 1). Следовательно, На рис. 2 показана величина , которая определяется из таблицы стандартного нормального распределения, так что Следовательно, размер резервного запаса должен удовлетворять неравенству B≥σL .
Слайд 5 Величина спроса на протяжении срока выполнения заказа L
обычно описывается плотностью распределения вероятностей, отнесенной к единице времени
(например, к дню или неделе), из которой можно определить распределение спроса на протяжен периода L. В частности, если спрос за единицу времени является нормально распределенной случайной величиной со средним D и стандартным отклонением σ, то общий спрос на протяжении срока выполнения заказа L будет иметь распределение N(μL, σL), где μL=DL и σL= . Формула для σL получена на основании того, что значение L является целым числом (или же округлено до целого числа). 1.2. Стохастический вариант модели экономичного размера заказа "Рандомизированная" модель экономичного размера заказа не дает оптимальную политику управления запасами. Информация, имеющая отношение к вероятностной природе спроса первоначально не учитывается, а используется лишь независимо на последнем этапе вычислений. Рассмотрим более точную модель, в которой вероятностная природа спроса учитывается непосредственно в постановке задачи.
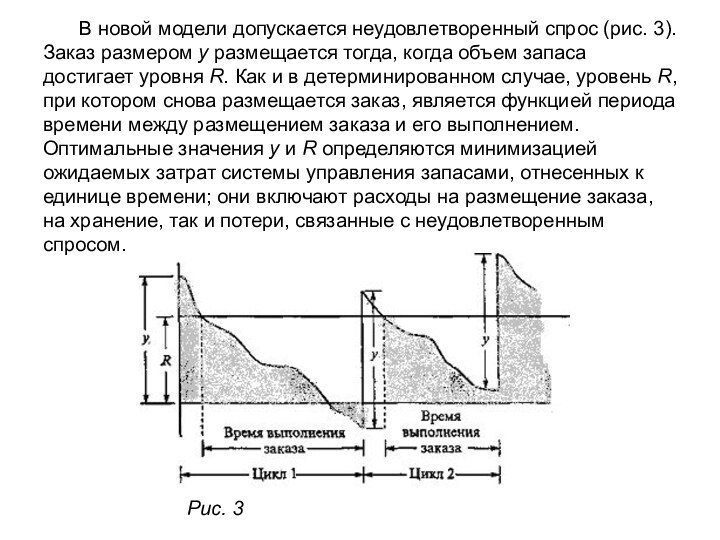
Слайд 6 В новой модели допускается неудовлетворенный спрос (рис. 3).
Заказ размером у размещается тогда, когда объем запаса достигает
уровня R. Как и в детерминированном случае, уровень R, при котором снова размещается заказ, является функцией периода времени между размещением заказа и его выполнением. Оптимальные значения у и R определяются минимизацией ожидаемых затрат системы управления запасами, отнесенных к единице времени; они включают расходы на размещение заказа, на хранение, так и потери, связанные с неудовлетворенным спросом. Рис. 3Слайд 7 В рассматриваемой модели приняты три допущения. 1. Неудовлетворенный
в течение срока выполнения заказа спрос накапливается. 2. Разрешается
не более одного невыполненного заказа. 3. Распределение спроса в течение срока выполнения заказа является стационарным (неизменным) во времени. Для определения функции, отражающей суммарные затраты, отнесенные к единице времени, введем следующие обозначения. ▪ f(x) — плотность распределения спроса х в течение срока выполнения заказа, ▪ D — ожидаемое значение спроса в единицу времени, ▪ h — удельные затраты на хранение (на единицу продукции за единицу времени), ▪ р — удельные потери от неудовлетворенного спроса (на единицу продукции за единицу времени), ▪ К — стоимость размещения заказа.Слайд 8 Основываясь на этих определениях, вычислим компоненты функции затрат. 1.
Стоимость размещения заказов. Приближенное число заказов в единицу времени
равно D/y, так что стоимость размещения заказов в единицу времени равна KD/y. 2. Ожидаемые затраты на хранение. Средний уровень запаса равен Следовательно, ожидаемые затраты на хранение за единицу времени равны hI. Приведенная формула получена в результате усреднения ожидаемых запасов в начале и конце временного цикла, т.е. величин у + M{R-х} и M{R-х} соответственно. При этом игнорируется случай, когда величина R - М{х} может быть отрицательной, что является одним из упрощающих допущений рассматриваемой модели.
Слайд 9 3. Ожидаемые потери, связанные с неудовлетворенным спросом. Дефицит
возникает при х > R. Следовательно, ожидаемый дефицит за
единицу времени равен Так как в модели предполагается, что р пропорционально лишь объему дефицита, ожидаемые потери, связанные с неудовлетворенным спросом, за один цикл равны pS. Поскольку единица времени содержит D/y циклов, то ожидаемые потери, обусловленные дефицитом, составляют pDS/y за единицу времени. Результирующая функция общих потерь за единицу времени TCU имеет следующий вид.
Слайд 10 Оптимальные значения у* и R* определяются из представленных
ниже уравнений. Следовательно, имеем
(1) (2) Так как из уравнений (1) и (2) у* и R* нельзя определить в явном виде, для их нахождения используется численный алгоритм, предложенный Хедли и Уайтин (Hadley, Whitin) [1]. Доказано, что алгоритм сходится за конечное число итераций при условии, что допустимое решение существует.
Слайд 11 При R = 0 последние два уравнения соответственно
дают следующее. Если ≥ ,
тогда существуют единственные оптимальные значения для у и R. Вычислительная процедура определяет, что наименьшим значением у* является , которое достигается при S = 0. Алгоритм состоит из следующих шагов. Шаг 0. Принимаем начальное решение и считаем R0 = 0. Полагаем i = 1 и переходим к шагу i. Шаг i. Используем значение уi для определения Ri, из уравнения (2). Если Ri≈ R i-1, вычисления заканчиваются; оптимальным решением считаем у* = уi и R* = Ri. Иначе используем значение Ri в уравнении (1) для вычисления уi. Полагаем i=i+1 и повторяем шаг i.
Слайд 12 2. Одноэтапные модели Одноэтапные модели управления запасами отражают ситуацию,
когда для удовлетворения спроса в течение определенного периода продукция
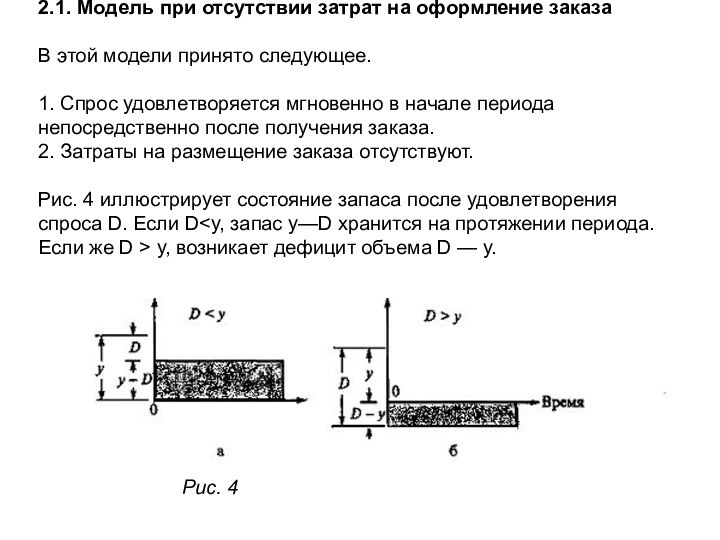
заказывается только один раз. Например, модный сезонный товар устаревает к концу сезона, и, следовательно, заказы на него могут не возобновляться. В данном разделе рассматривается два типа таких моделей: с учетом и без учета затрат на оформление заказов. При изложении данного материала используются следующие обозначения. с — стоимость закупки (или производства) единицы продукции, К — стоимость размещения заказа, h — удельные затраты на хранение единицы продукции в течение рассматриваемого периода, р — удельные потери от неудовлетворенного спроса (на единицу продукции за рассматриваемый период), D — величина случайного спроса за рассматриваемый период, f(D) — плотность вероятности спроса за рассматриваемый период, у — объем заказа, х — наличный запас продукта перед размещением заказа. Модель определяет оптимальный объем заказа у, который минимизирует суммарные ожидаемые затраты, связанные с закупкой (или производством), хранением и неудовлетворенным спросом. При известном оптимальном значении у (обозначается у*) оптимальное управление запасами состоит в размещении заказа объемом у* - х, если х < y; в противном случае заказ не размещается.Слайд 13 2.1. Модель при отсутствии затрат на оформление заказа В
этой модели принято следующее. 1. Спрос удовлетворяется мгновенно в начале
периода непосредственно после получения заказа. 2. Затраты на размещение заказа отсутствуют. Рис. 4 иллюстрирует состояние запаса после удовлетворения спроса D. Если DСлайд 14 Ожидаемые затраты М{С(у)} на период выражаются следующей формулой. Можно
показать, что функция М{С(у)} является выпуклой по у и,
таким образом, имеет единственный минимум. Следовательно, вычисляя первую производную функции М{С(у)} по у и приравнивая ее к нулю, получим или Отсюда имеем Правая часть последней формулы известна как критическое отношение. Значение у* определено только при условии, что критическое отношение неотрицательно, т.е. . Случай, когда , является бессмысленным, так как это предполагает, что стоимость закупки единицы продукции выше потери от неудовлетворенного спроса.
Слайд 15 Ранее предполагалось, что спрос D является непрерывной случайной
величиной. Если же D является дискретной величиной, то плотность
распределения вероятностей f(D) определена лишь в дискретных точках и функция затрат определяется в соответствии с формулой. Необходимыми условиями оптимальности являются неравенства М{С(у - 1)} ≥ М{С(у)} и М{С(у + 1)} ≥ М{С(у)}. Эти условия в данном случае являются достаточными, так как функция М{С(у)} выпукла. Применение этих условий после некоторых алгебраических преобразований приводит к следующим неравенствам для определения у*.
Слайд 16 2.2. Модель при наличии затрат на оформление заказа Данная
модель отличается от выше представленной тем, что учитывается стоимость
К размещения заказа. Используя обозначения, введенные выше, получаем следующее выражение для суммарной ожидаемой стоимости. Как показано в разделе 2.1, оптимальное значение y* должно удовлетворять соотношению
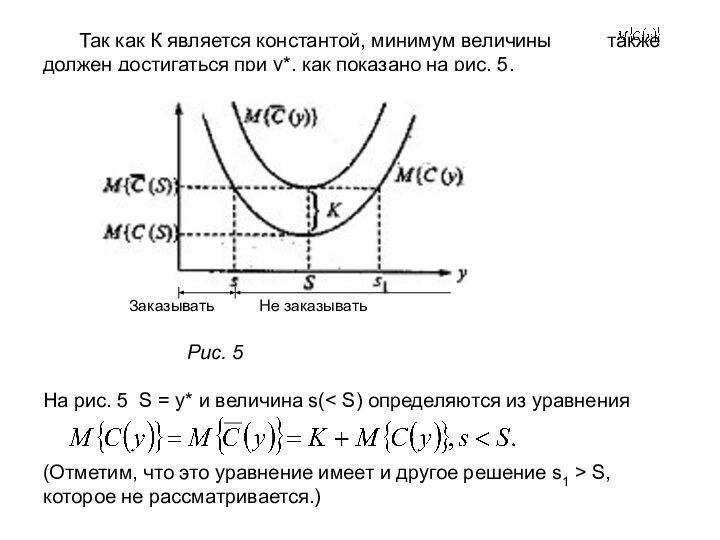
Слайд 17 Так как К является константой, минимум величины
также должен достигаться при у*, как
показано на рис. 5. Заказывать Не заказывать Рис. 5 На рис. 5 S = y* и величина s(< S) определяются из уравнения (Отметим, что это уравнение имеет и другое решение s1 > S, которое не рассматривается.)
Слайд 18 Задача формулируется следующим образом. Какое количество продукции необходимо
заказывать, если наличный запас перед размещением заказа составляет х
единиц? Ответ на этот вопрос рассматривается по отдельности при выполнении следующих условий. 1. x
Слайд 19 Случай 2 (s≤x≤S). Из рис. 5 видно, что Следовательно,
в данном случае дополнительных затрат не возникает, если новый
заказ не размещается. Поэтому у* =х. Случай 3 (х> S). Из рис. 5 видно, что при у > х Это неравенство показывает, что в данном случае экономнее будет не размещать заказ, т.е. у*=х. Описанная стратегия управления запасами, часто именуемая (s-S)-стратегией, определяется следующим правилом. Если х < s, делать заказ объемом S - х, если х ≥ s, заказывать не следует. (Оптимальность (s-S)-стратегии следует из того, что соответствующая функция затрат является выпуклой. Если это свойство не выполняется, данная стратегия перестает быть оптимальной.)
Слайд 20 3. Многоэтапные модели Рассматривается многоэтапная модель в предположении, что
не учитывается стоимость размещения заказа. Кроме того, в модели
предусматривается возможность задолженности и нулевое время поставки. Предполагается также, что спрос D в каждый период описывается стационарной (независящей от времени) плотностью вероятности f(D). В многоэтапной модели учитывается приведенная стоимость денег. Если α (< 1) – коэффициент дисконтирования (процент скидки) для одного этапа, то сумма А спустя n этапов будет эквивалентна сумме α n А в настоящий момент. Предположим, что горизонт планирования охватывает n этапов и неудовлетворенный спрос может оставаться таковым лишь на протяжении одного этапа. Пусть Fi(xi) — максимальная суммарная ожидаемая прибыль для этапов от i до n, определенная при условии, что хi — уровень имеющегося запаса перед размещением заказа на i-м этапе.Слайд 21 Используя обозначения из раздела 2 и предполагая, что
r — удельный доход от реализации единицы продукции, сформулируем
задачу управления запасами в виде следующей задачи динамического программирования. где F n+1 (yn-D) ≡ 0. Величина xi может принимать отрицательные значения, так как неудовлетворенный спрос может накапливаться. Величина αr(D-yi) включена во второй интеграл, поскольку D-yi представляет собой неудовлетворенный спрос на i-м этапе, который должен быть удовлетворен на этапе i+1 .
Слайд 22 Задачу можно решить рекуррентно методами динамического программирования. Если
число этапов является бесконечным (бесконечный горизонт планирования), приведенное выше
рекуррентное уравнение сводится к следующему. где х и у представляют собой уровни запаса на каждом этапе до и после получения заказа соответственно. Оптимальное значение у можно определить из приведенного ниже необходимого условия, которое в данном случае есть также достаточным, так как функция ожидаемой прибыли F(x) является вогнутой.
Слайд 23 Величина определяется следующим образом. Если на начало следующего этапа
уровень запаса еще составляет β (> 0) единиц, то
прибыль на этом этапе возрастает на величину cβ, так как объем последующего заказа уменьшается именно на эту величину. Это означает, что Следовательно, необходимое условие принимает вид Поэтому оптимальный уровень заказа у* определяется из уравнения Оптимальная стратегия каждого этапа при заданном исходном запасе х выражается следующим правилом. Если х < у*, делать заказ объемом у* - х, если х ≥ у*, заказа не делать.
Слайд 24 4. Заключение В моделях управления запасами спрос является случайным.
Предложен широкий спектр методов решения построенных моделей — от
вероятностной (рандомизированной) версии детерминированной модели экономичного размера заказа до более сложных, связанных с применением методов динамического программирования. Литература Хедли Дж., Уайтин Т. Анализ систем управления запасами.— М: Наука, 1969.) Кофман А. Методы и модели исследования операций. — М.: Мир, 1966.
Слайд 25
Основные соотношения СМО
В теории МО обычно рассматривается один
параметр – время. Базовый случайный процесс – пуассоновский.
Распределение Пуассона
,где Pn(t) – вероятность того, что за промежуток t поступит n требований.
Свойства:
е-λt - вероятность отсутствия требований в интервале t;
λt(e-λt) - вероятность поступления одного требования за время t;
следовательно вероятность поступления за время t более одного требования
т.е. функция, которая ведет себя как t2.
Отсюда следует, что при малых t, все члены с t2 - пренебрежимо малы.
При малых t вероятность наступления более одного требования пренебрежимо мала
Слайд 26 Рассмотрим стационарный режим. Понятие стационарного состояния классически поясняется
в решении двух задач МО: - модель Эрланга (изменение
Pn(t) в зависимости от t описывается Pn/(t), т.е. Pn/(t) = 0); - формула Поллачека- Хинчина (из рассмотрения , что также приводит к Pn(t), не зависящим от t.(1) - исходные выражения для
пуассоновского распределения
Слайд 27 Модель Эрланга Допущения: -процесс начинается при отсутствии требований в очереди; -
СМО с пуассоновским входящим потоком с параметром λ; - экспоненциальное
время обслуживания с параметром μ; - дисциплина очереди FIFO. Исходные уравнения Замечание: член, содержащий (∆t)2 опускается. Поэтому, например, выражение (1-λ∆t)(1-μ∆t) (за время ∆t в систему не поступит и не покинет ни одно требование) преобразуется в 1-(λ+μ)∆t.(2)
Слайд 28 Перенесем Pn(t) в левую часть и при ∆t→0
имеем Исследуем стационарное состояние, приравняв производные по времени к
нулю. Введем понятие загрузки системы α = λ/μ. Если λ/μ ≥1, то число ожидающих требований растет неограниченно и стационарный режим не устанавливается . Для стационарного состояния при λ/μ <1 найдем выражения для : - математического ожидания числа требований, находящихся в очереди; - среднего времени ожидания.(3)
Слайд 29 Приравняв к нулю производные в (3), получим: Учитывая, что
α=λ/μ преобразуем (4) Пусть в первом уравнении системы (5) n=1.
Тогда (1+α)P1=P2+αP0 и, учитывая, что P1=αP0, имеем P2=α2P0. Повторяя этот процесс, получаем Pn=αnP0. (6) Напомним, что , поэтому или , откуда P0=1-α и Pn= αn(1-α) (7) Выражение (7) представляет собой геометрическое распределение.(4)
(5)
Слайд 30 Математическое ожидание (L) числа требований, находящихся в системе
(с учетом (7))
Математическое ожидание числа требований, находящихся в очереди
(8)
(9)
Слайд 31 Формула Поллачека-Хинчина Рассматривается одноканальная СМО,
находящаяся в стационарном режиме с входным пуассоновским случайным процессом
с параметром λ. Время обслуживания имеет произвольное распределение с интенсивностью μ клиентов в ед. времени. Дисциплина очереди FIFO. Анализируем стационарный режим при λ/μ < 1; t→∞. q/ = max (q-1,0)+r = q-1+δ+r, δ(q)= «δ» вводится, чтобы не использовать символ max.остается q
клиентов
q-1
время
t – время
обслуживания
клиентов
моменты времени,
когда обслуженные
клиенты попадают
в систему и начало
обслуживания новых
0, если q>0
1, если q=1
↑ r клиентов поступает в систему





























