Презентация на тему Решение задач из части С по теме Электромагнитные колебания физика 11 класс

Идеальным?
Какие колебания называются свободными?
Какие колебания называются гармоническими?
Что такое собственная

циклическая частота колебательной системы?
Что называется периодом колебаний?
Что называется амплитудой колебаний? 
Что такое фаза колебаний?
По какой формуле рассчитать энергию электрического поля?
По какой формуле рассчитать энергию магнитного поля?
Чему равна полная энергия?

тока и напряжения, сопровождающиеся взаимными превращениями энергии электрического и

магнитного полей
Замкнутая электрическая цепь, состоящая из конденсатора емкости С и катушки индуктивности L, называется колебательным контуром. Если сопротивление проводов =0, то контур называется идеальным
Колебания возникающие в системе под действием внутренних сил, называются свободными
Периодические изменения физической величины, происходящие по закону синуса или косинуса в зависимости от времени, называются гармоническими колебаниями
Величина ω=2πν, равная числу колебаний за 2π секунд, называется собственной циклической частотой
Период колебаний – это время , в течение которого совершается одно полное колебание
Наибольшее значение колеблющейся величины называется амплитудой колебаний
Аргумент косинуса или синуса в уравнении φ=(ω0t+ φ0) называется фазой колебаний

Или (1)
q- заряд на обкладках конденсатора
собственная круговая частота колебаний заряда
(2)
Период и частота колебаний в -контуре (Формула Томсона):
(3)
L- Индуктивность катушки контура,
C – Емкость конденсатора.
Мгновенные значения заряда, напряжения и силы тока в колебательном контуре меняются по закону:
q= (4)
U= (5)
I= (6)
- амплитудные значения заряда на конденсаторе, напряжение на нем и силы тока в колебательном контуре, круговая частота собственных колебаний; время отсчитывается от момента максимальной зарядки конденсатора.
Величина электродвижущей силы, напряжения и силы переменного тока зависят от времени по закону:
или (7)
U= или U=
I= (9)
начальная фаза колебаний , которая зависит от момента, с которого ведется отсчет времени.

Связь действующих значений силы тока, напряжения и ЭДС с амплитудными значениями:
(10)

Сопротивление конденсатора в цепи переменного тока
(11)
Сопротивление катушки в цепи переменного тока
(12)
Величина сопротивления цепи переменного тока, содержащей последовательное соединение резистора, конденсатора и катушки индуктивности:
(13)
Величина Z называется импедансом цепи.
Закон Ома для цепи переменного тока:
(14)
Сдвиг по фазе между силой тока и напряжением в такой цепи определяется формулой
(15)
Или
(15/1)
Средняя мощность, выделяющаяся в цепи переменного тока,
(16)
Коэффициент трансформации трансформатора:ᵑ
(17)

- ЭДС самоиндукции в первичной и ЭДС индукции во вторичной обмотках трансформатора, - число витков в первичной и вторичной обмотках трансформатора, соответственно. Если сопротивлениие проводов первичной и вторичной обмоток малы , то можно считать, что ε~U и . При этом коэффициент трансформации определяется формулой
. (18)

Коэффициент полезного действия трансформатора :
η= (19)
Если потери в трансформаторе малы, то , и можно записать, что мощность во вторичной и первичной катушках примерно одинаковы:
, или, (20)

- напряжение, поданное на первичную обмотку трансформатора,
- напряжение, снимаемое со вторичной обмотки.
Потеря энергии происходит на активном сопротивлении.

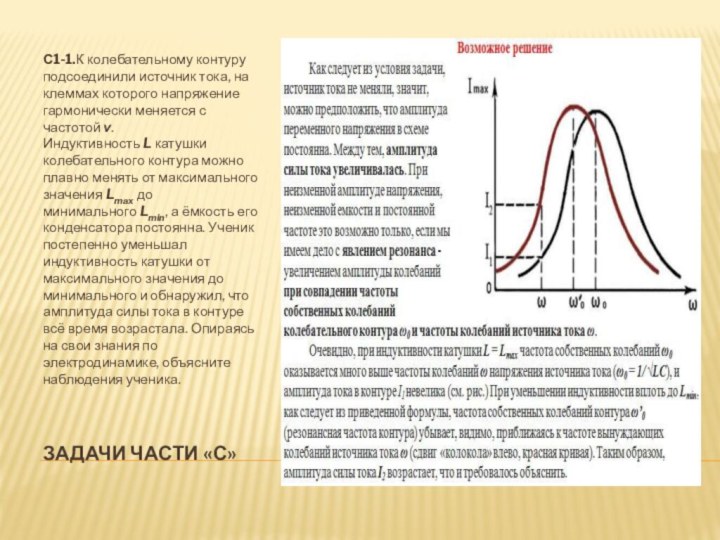
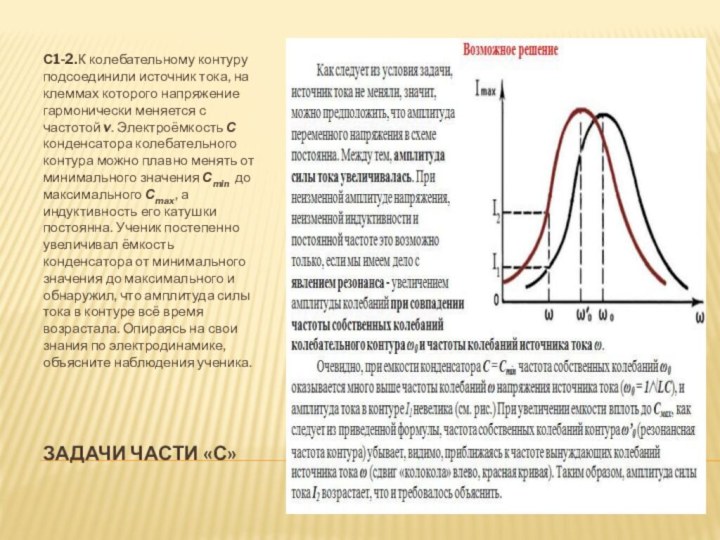
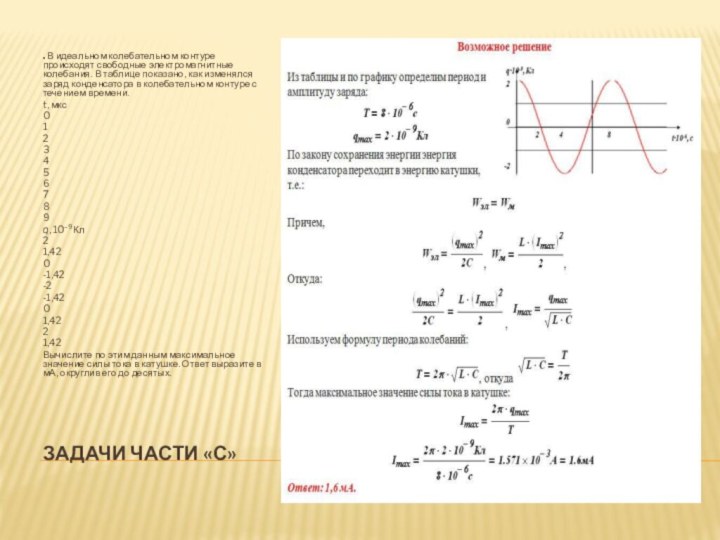
в колебательном контуре:
Определяется связь между величинами емкости, индуктивности и

параметрами возникших колебаний (T, V, ), решаются с использованием формул 2 и 3.
К ним в соответствии с данными задачи, могут быть добавлены формулы, связывающие частоту или период, длину возникшей волны и скорость электромагнитных волн:
c=λ/Т= λν,
c-скорость электромагнитных волн, в вакууме 3м/с.
Для измерения собственной частоты колебаний контура, помимо конденсатора постоянной емкости, последовательно или параллельно ему включают конденсатор переменной емкости. Обычно для таких случаев требуется рассчитать диапазон частот, которые возникают в контуре: (или диапазон длин волн). Для расчета эквивалентной емкости С контура надо вспомнить формулы для последовательного соединения конденсаторов,

И для параллельного соединения :
С=
Иногда в таких случаях нужна формула емкости плоского конденсатора
.
2Для идеального колебательного контура справедлив закон сохранения энергии. Поэтому в любой момент времени в течении периода энергия в контуре одна и та же и равна начальному запасу энергии:
W=const, или
При максимальном заряде на обкладках конденсатора (и соответственно, максимальном значении напряжения) энергия контура сосредоточена в электрическом поле конденсатора и равна
В промежуточные моменты времени имеются и электрическая энергия , и магнитная , но их сумма постоянна:
,
W- величина полной электромагнитной энергии колебательного контура. Последнее соотношение можно использовать для решения задач, в которых даны или требуется найти амплитудные или мгновенные значения силы тока, напряжения или заряда на конденсаторе.

3. Все задачи, в которых задана аналитическая или графическая зависимость от времени ЭДС , силы тока I, напряженияU и заряда q решаются точно так же, как и задачи такого типа на механические колебания. Задачи, в которых по заданной аналитической зависимости надо найти амплитуду, круговую частоту и начальную фазу, решаются просто сопоставлением данного уравнения с соответствующим уравнением в общем виде (4-9). Для определения периода и частоты используются формулы T=1/ν, T=t/n, ν=n/t, где n- количество колебаний за время t.
4 В задачах о переменном токе мы рассматриваем только технический (синусоидальный) ток.
Во всех случаях, когда указаны значения ℰ,I,U, и нет специальных указаний, речь идет о действующих (или эффективных) значениях этих величин. Если надо найти амплитудные значения, то они для гармонических колебаний связаны с действующими значениями формулами 10.
Задачи на расчет цепей переменного тока решаются по закону Ома (14).
Цепи переменного тока кроме активного сопротивления R содержат емкостное и индуктивное сопротивления, которые определяются формулами (11)и (12); полное сопротивление Z цепи переменного тока (импеданс) рассчитывается по формуле (13).
Нельзя забывать о том, что в цепях переменного тока имеется сдвиг по фазе между силой тока и напряжением. Его вычисляют по формулам (15) и (15/1), используя затем таблицы тригонометрических функций.
В цепи, содержащей активное и реактивное сопротивления, мощность выделяется только на активном сопротивлении. Значение мощности будет меньше, чем на том же активном сопротивлении в отсутствии реактивных элементов – конденсатора и катушки. Это определяется сдвигом мгновенных значений силы тока и напряжения по фазе. Формула для вычисления мощности в цепи с активным и реактивным сопротивлениями (16) имеет вид , - сдвиг фаз между силой тока и наряжением; – коэффициент мощности. Значение можно найти по формуле (15/1) или сначала найти tgи по формуле (15) и воспользоваться тригонометрическими таблицами.

основными являются формулы (17)-(20). Формула (17) – используется для

режима холостого хода, (18) – в случаях, когда падением напряжения на витках вторичной обмотки нагруженного трансформатора можно пренебречь. При больших токах во вторичной цепи необходимо записать следующее:

- напряжение на зажимах вторичной обмотки, –сила тока во вторичной обмотке, r – ее сопротивление. В таких случаях коэффициент трансформации .
Небольшую группу составляют задачи на передачу энергии переменного тока от генератора к потребителю. Полная схема электрической цепи, соответствующая этим случаям, представлена на рисунке 1. Она состоит из генератора переменного напряжения, дающего электродвижущую силу ℰ, повышающего трансформатора 1, линии электропередач (ЛЭП), понижающего трансформатора 2, потребителя электроэнергии (нагрузки) - . решаются обычно по этапам.




IНа первом этапе рассматривается генератор переменного напряжения и повышающий трансформатор I. ЭДС генератора ℰ равна сумме падений напряжения на внутреннем сопротивлении генератора и на первичной обмотке повышающего трансформатора: ℰ= .

Часто дается не значение ЭДС ℰ, а падение напряжения на зажимах генератора. Оно равно величине ℰ минус падение напряжение внутри генератора, то есть напряжению на первичной обмотке трансформатора I. Если сопротивлением первичной обмотки по условию задачи можно пренебречь, то можно использовать формулы (17 )и(18).
II На втором этапе рассматриваются оба трансформатора и линия электропередачи. ЭДС индукции, которая наводится н вторичной обмотке первого трансформатора, равна сум падений напряжений:

падение напряжения на вторичной обмотке первого трансформатора, – падение напряжения на проводах, ,- напряжение на первичной обмотке второго трансформатора.
Сопротивление проводов или силу тока в проводах часто приходится находить используя формулу мощности тепловых потерь или закон Джоуля – Ленца: – сопротивление проводов линии электропередачи.
Вычисляя R по R=ρl/s формуле , следует учесть, что длина провода равна удвоенному расстоянию от повышающего трансформатора до понижающего (или от генератора до нагрузки).
Сила тока одинакова во вторичной обмотке первого трансформатора, на проводах и на первичной обмотке второго трансформатора.
III На третьем этапе (второй трансформатор-нагрузка)можно использовать кроме формул (17) (18) еще и (20). Кроме того, мощность потерь на проводах можно найти по формуле
В случаях, если какой- либо элемент полной цепи отсутствует, то соответственно падение напряжения и сопротивления следует опустить, что упростит задачу. Если в задаче дан коэффициент полезного действия линии электропередачи, то он равен отношению мощности полезной, то есть нагрузке , к мощности, которую дает генератор :

на клеммах которого напряжение гармонически меняется с частотой ν. Индуктивность L катушки

колебательного контура можно плавно менять от максимального значения Lmax до минимального Lmin, а ёмкость его конденсатора постоянна. Ученик постепенно уменьшал индуктивность катушки от максимального значения до минимального и обнаружил, что амплитуда силы тока в контуре всё время возрастала. Опираясь на свои знания по электродинамике, объясните наблюдения ученика.  

на клеммах которого напряжение гармонически меняется с частотой v. Электроёмкость С

конденсатора колебательного контура можно плавно менять от минимального значения Сmin  до максимального Сmax, а индуктивность его катушки постоянна. Ученик постепенно увеличивал ёмкость конденсатора от минимального значения до максимального и обнаружил, что амплитуда силы тока в контуре всё время возрастала. Опираясь на свои знания по электродинамике, объясните наблюдения ученика.  

емкостью 20 мкФ и катушки индуктивностью 8 мГн. Амплитуда колебаний заряда конденсатора 8 нКл.

Какова амплитуда колебаний силы тока в контуре?

силы тока в катушке индуктивности Im = 10 мА, а амплитуда

напряжения на конденсаторе Um= 4,0 В. В момент времени t напряжение на конденсаторе равно 3,2 В. Найдите силу тока в катушке в этот момент.

силы тока в катушке индуктивности Im = 5 мА, а амплитуда

напряжения на конденсаторе Um = 2,0 В. В момент времени t напряжение на конденсаторе равно 1,2 В. Найдите силу тока в катушке в этот момент.  

электромагнитные колебания. В таблице показано, как изменялся заряд конденсатора

в колебательном контуре с течением времени.
t, мкс
0
1
2
3
4
5
6
7
8
9
q, 10–9 Кл
2
1,42
0
-1,42
-2
-1,42
0
1,42
2
1,42
Вычислите по этим данным максимальное значение силы тока в катушке. Ответ выразите в мА, округлив его до десятых.

конденсатора и катушки индуктивности, амплитуда силы тока Im = 50 мА.

В таблице приведены значения разности потенциалов на обкладках конденсатора, измеренные с точностью до 0,1 В в последовательные моменты времени.
t, мкс
0
1
2
3
4
5
6
7
8
U, В
0,0
2,8
4,0
2,8
0,0
–2,8
–4,0
–2,8
0,0
Найдите значение электроёмкости конденсатора.  

момент времени напряжение на конденсаторе равно 1,2 В, а сила

тока в катушке индуктивности равна 4 мА. Амплитуда колебаний силы тока в катушке равна 5 мА. Найдите амплитуду колебаний напряжения на конденсаторе.

ЭДС источника тока равна 12 В, емкость конденсатора 2 мФ, индуктивность

катушки5 мГн, сопротивление лампы — 5 Ом и сопротивление резистора 3 Ом. В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Внутренним сопротивлением источника тока пренебречь. Сопротивлением катушки и проводов пренебречь.