- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по физике на тему Механические колебания
Содержание
- 2. Механическими колебаниями называются движения, которые точно
- 3. Условия возникновения механических колебанийВывести тело из положения
- 4. График механических колебаний
- 5. Виды колебаний1) Свободные колебания - возникают под
- 6. Виды колебаний2) Вынужденные колебания – происходят под
- 7. Величины, характеризующие механические колебания.Ф-11-В Механические колебания. Характеристики механического колебания
- 8. Величины, характеризующие механические колебания.1). Смещение – это
- 9. Величины, характеризующие механические колебания. 2). Амплитуда
- 10. Величины, характеризующие механические колебания.3). Период – это
- 11. Величины, характеризующие механические колебания.4). Частота – это
- 12. Величины, характеризующие механические колебания.5). Циклическая частота –
- 13. Величины, характеризующие механические колебания.6). Фаза колебаний –
- 14. Гармонические колебанияэто колебания, при которых изменения физических
- 15. Задача № 1Дано:Найти: Х, Хm, Т, , ω, φРешение:t . c
- 16. Задача № 1Дано:Найти: Х, Хm, Т,
- 17. Задача № 1Дано:Найти: Х, Хm, Т,
- 18. Задача № 1Дано:Найти: Х, Хm, Т,
- 19. Задача № 1Дано:Найти: Х, Хm, Т,
- 20. Задача № 1Дано:Найти: Х, Хm, Т,
- 21. Задача № 1Дано:Найти: Х, Хm, Т,
- 22. Задача № 1Дано:Найти: Х, Хm, Т,
- 23. Задача № 1Дано:Найти: Х, Хm, Т,
- 24. Задача № 1Дано:Найти: Х, Хm, Т,
- 25. Задача № 1Дано:Найти: Х, Хm, Т,
- 26. Задача № 1Дано:Найти: Х, Хm, Т,
- 27. Задача № 1Дано:Найти: Х, Хm, Т,
- 28. Задача № 1Дано:Найти: Х, Хm, Т,
- 29. Задача № 1Дано:Найти: Х, Хm, Т,
- 30. Колебательные системыМатематический маятник – материальная точка, подвешенная
- 31. Колебательные системы2) Пружинный маятник – это груз,
- 32. Колебательные системы3) Баллистический маятник (Ф-10-В )
- 33. Превращение энергии при механических колебаниях
- 34. Резонанс
- 35. Резонанс
- 36. Резонанс Резонанс – это явление возрастания амплитуды
- 37. Резонанс С энергетической точки зрения создаются наилучшие
- 38. Применение резонанса:Для измерения частоты вибраций (частотомеры)В акустикеПри
- 40. Опыт ФукоЗдание Парижского Пантеона в центре
- 41. Опыт ФукоВ России маятник Фуко длиной 98 м
- 42. Скачать презентацию
- 43. Похожие презентации
Механическими колебаниями называются движения, которые точно или приблизительно повторяются через одинаковые промежутки времени Ф-11-В Свободные и вынужденные колебания































Слайд 2
Механическими колебаниями
называются движения, которые точно или
приблизительно повторяются через одинаковые промежутки времени
вынужденные колебания
Слайд 3
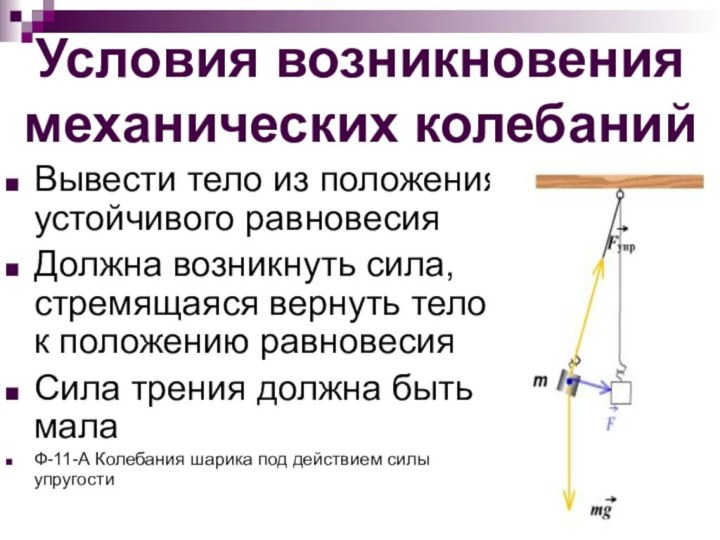
Условия возникновения механических колебаний
Вывести тело из положения устойчивого
равновесия
Должна возникнуть сила, стремящаяся вернуть тело к положению равновесия
Сила
трения должна быть малаФ-11-А Колебания шарика под действием силы упругости
Слайд 5
Виды колебаний
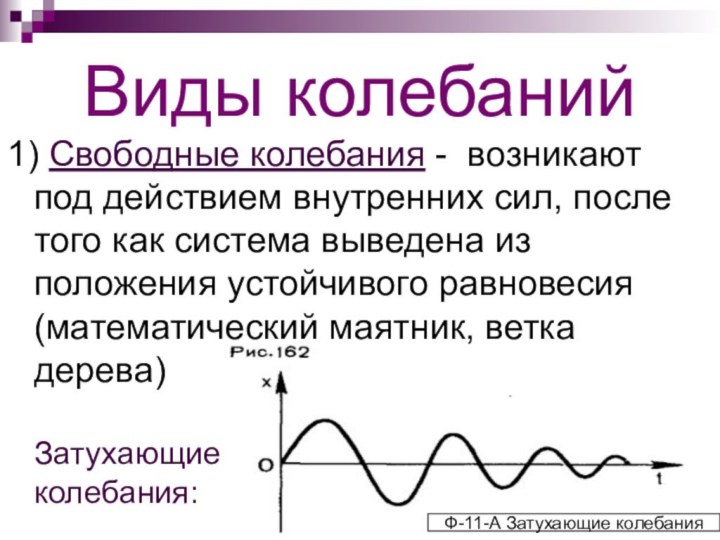
1) Свободные колебания - возникают под действием
внутренних сил, после того как система выведена из положения
устойчивого равновесия (математический маятник, ветка дерева) Затухающие колебания:Ф-11-А Затухающие колебания
Слайд 6
Виды колебаний
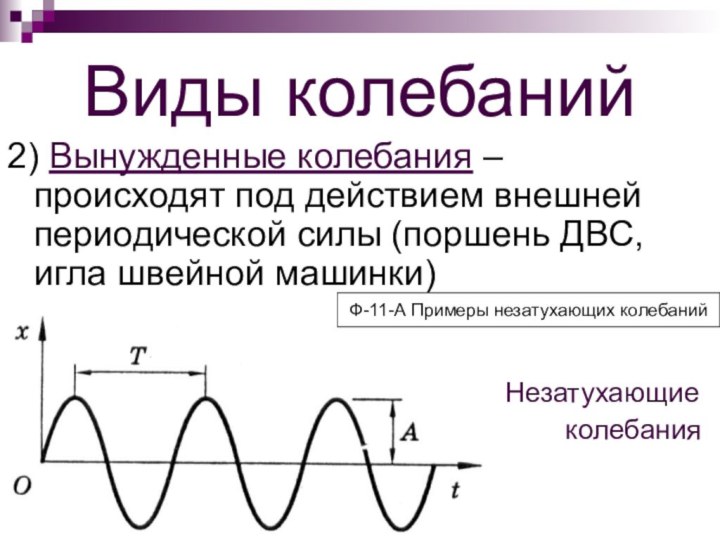
2) Вынужденные колебания – происходят под действием
внешней периодической силы (поршень ДВС, игла швейной машинки)
Незатухающие
колебания
Ф-11-А Примеры незатухающих колебаний
Слайд 7
Величины, характеризующие механические колебания.
Ф-11-В Механические колебания. Характеристики механического
колебания
Слайд 8
Величины, характеризующие механические колебания.
1). Смещение – это отклонение
колеблющейся точки от положения равновесия в данный момент времени
Х – смещение – [ м ]
Слайд 9
Величины, характеризующие механические колебания.
2). Амплитуда –
это наибольшее смещение точки от положения равновесия (при незатухающих
колебаниях амплитуда постоянна)Хm – амплитуда – [ м ]
Слайд 10
Величины, характеризующие механические колебания.
3). Период – это время
одного полного колебания
Т– период – [ с ]
n –
количество колебаний - [ ]t – все время движения - [ с ]
Слайд 11
Величины, характеризующие механические колебания.
4). Частота – это число
полных колебаний за единицу времени
(ню) – частота
– [ Гц ] (Герц)
Слайд 12
Величины, характеризующие механические колебания.
5). Циклическая частота – это
число полных колебаний, которые совершаются за 2π секунд
ω –
циклическая частота – [ ]
Слайд 13
Величины, характеризующие механические колебания.
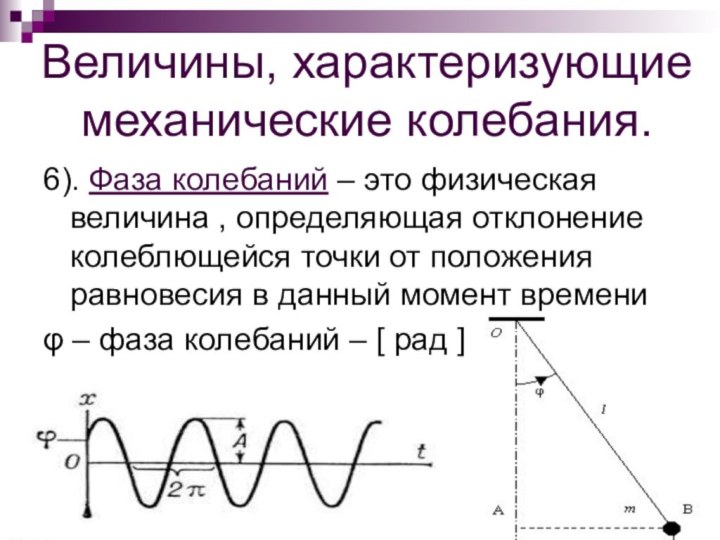
6). Фаза колебаний – это
физическая величина , определяющая отклонение колеблющейся точки от положения
равновесия в данный момент времениφ – фаза колебаний – [ рад ]
Слайд 14
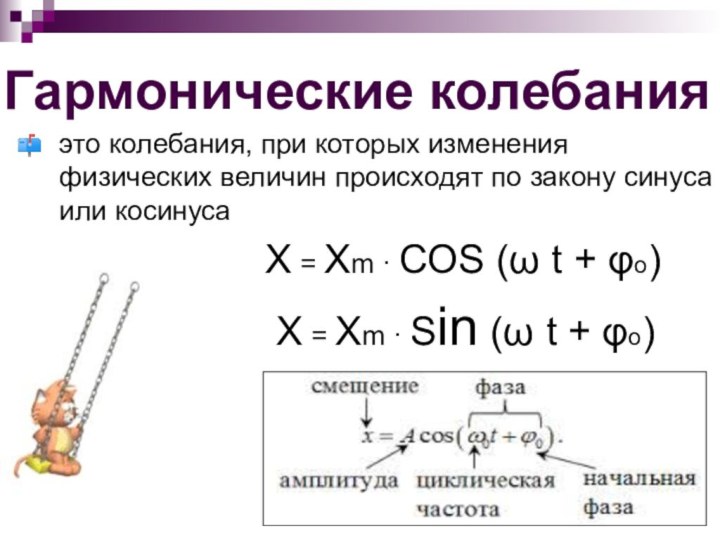
Гармонические колебания
это колебания, при которых изменения физических величин
происходят по закону синуса или косинуса
Х = Хm · СОS (ω t + φо)Х = Хm · Sin (ω t + φо)
Слайд 19
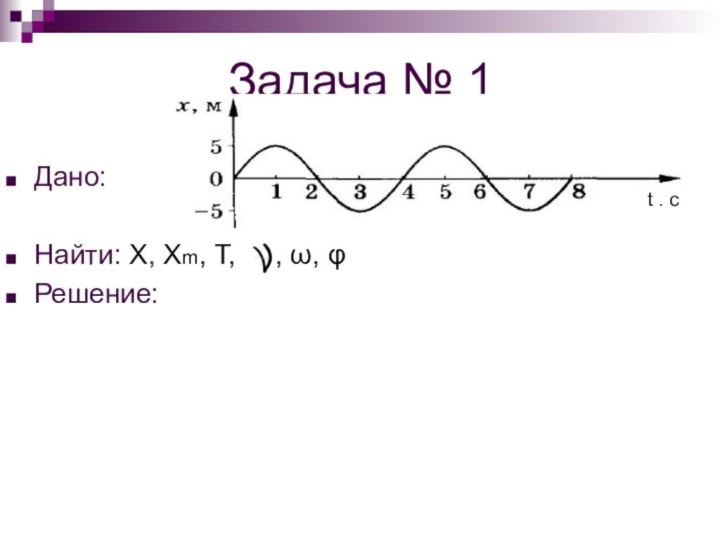
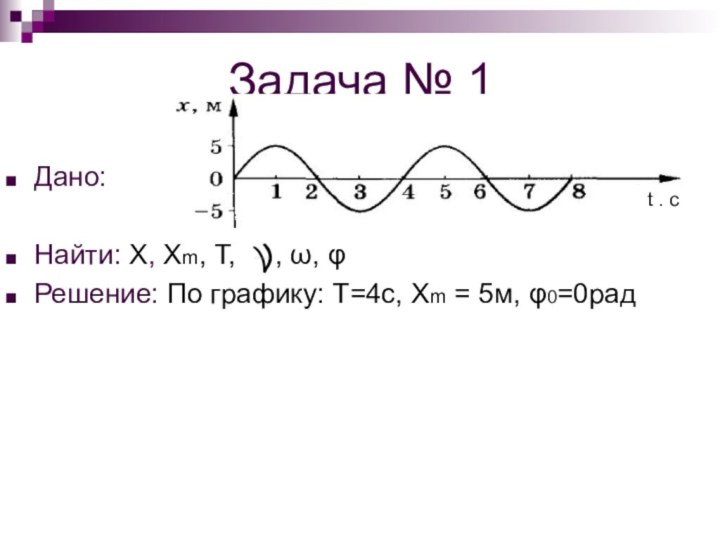
Задача № 1
Дано:
Найти: Х, Хm, Т,
, ω, φ
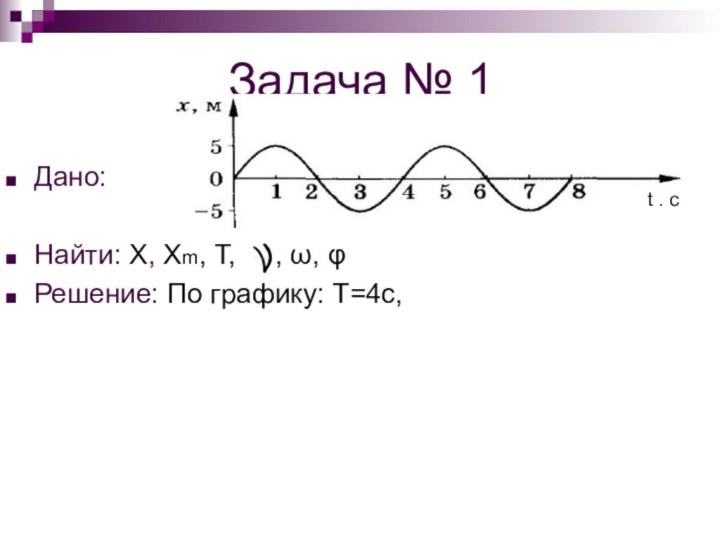
Решение: По графику: Т=4с, Хm = 5м,
φ0=0радС помощью формул:
t . c
Слайд 20
Задача № 1
Дано:
Найти: Х, Хm, Т,
, ω, φ
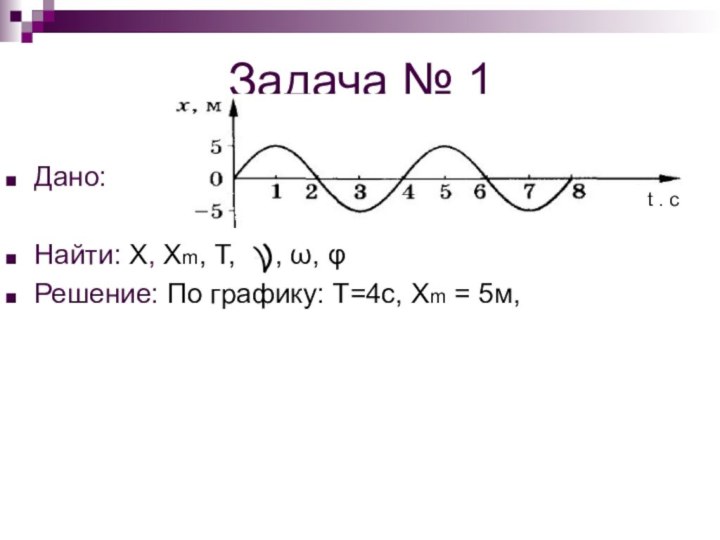
Решение: По графику: Т=4с, Хm = 5м,
φ0=0радС помощью формул: Гц
t . c
Слайд 21
Задача № 1
Дано:
Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м,
φ0=0радС помощью формул: Гц
ω =2π
t . c
Слайд 22
Задача № 1
Дано:
Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м,
φ0=0радС помощью формул: Гц
ω =2π =2∙π∙0,25
t . c
Слайд 23
Задача № 1
Дано:
Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м,
φ0=0радС помощью формул: Гц
ω =2π =2∙π∙0,25=0,5π
t . c
Слайд 24
Задача № 1
Дано:
Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м,
φ0=0радС помощью формул: Гц
ω =2π =2∙π∙0,25=0,5π
Х = Хm · sin (ω t + φо) =
t . c
Слайд 25
Задача № 1
Дано:
Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м,
φ0=0радС помощью формул: Гц
ω =2π =2∙π∙0,25=0,5π
Х = Хm · sin (ω t + φо) = 5
t . c
Слайд 26
Задача № 1
Дано:
Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м,
φ0=0радС помощью формул: Гц
ω =2π =2∙π∙0,25=0,5π
Х = Хm · sin (ω t + φо) = 5 · sin (
t . c
Слайд 27
Задача № 1
Дано:
Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м,
φ0=0радС помощью формул: Гц
ω =2π =2∙π∙0,25=0,5π
Х = Хm · sin (ω t + φо) = 5 · sin (0,5π t
t . c
Слайд 28
Задача № 1
Дано:
Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м,
φ0=0радС помощью формул: Гц
ω =2π =2∙π∙0,25=0,5π
Х = Хm · sin (ω t + φо) = 5 · sin (0,5π t )
t . c
Слайд 29
Задача № 1
Дано:
Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м,
φ0=0радС помощью формул: Гц
ω =2π =2∙π∙0,25=0,5π
Х = Хm · sin (ω t + φо) = 5 · sin (0,5π t )
Ответ:Т=4с, Хm =5м, φ0=0рад, ω=0,5π =0,25Гц
Х = 5 · sin (0,5π t )
t . c
Слайд 30
Колебательные системы
Математический маятник – материальная точка, подвешенная
на
невесомой нерастяжимой нити
- длина маятника – [ м ]g – ускорение свободного падения
g = 9,8 м/с²
Слайд 31
Колебательные системы
2) Пружинный маятник –
это груз, подвешенный
на
пружине
k–жесткость пружины-[Н/м]
m – масса груза –[кг]
Ф-11-В Пружинный маятник
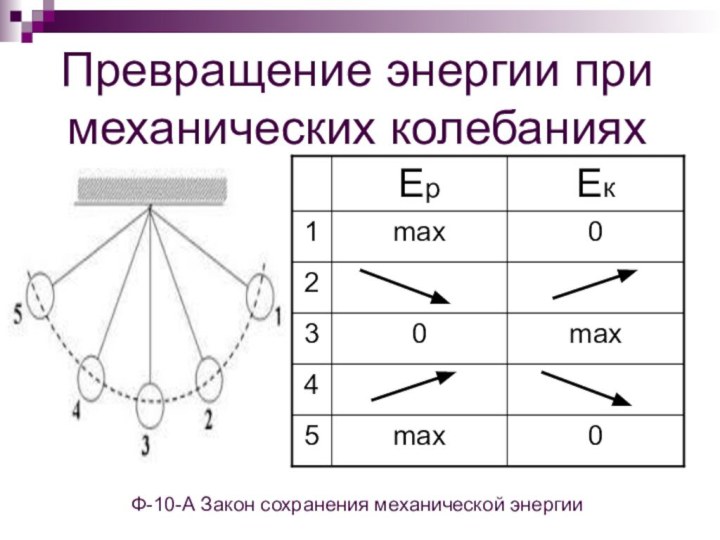
Слайд 33 Превращение энергии при механических колебаниях Ф-10-А Закон сохранения механической
энергии
Слайд 36
Резонанс
Резонанс – это явление возрастания амплитуды колебаний
при приближении частоты вынуждающей силы к собственной частоте колебательной
системы.Примеры: качели
Ф-11-В Явление механического резонанса
Слайд 37
Резонанс
С энергетической точки зрения создаются наилучшие условия
для передачи энергии от внешнего источника к колебательной системе.
Слайд 38
Применение резонанса:
Для измерения частоты вибраций (частотомеры)
В акустике
При расчетах
балок, мостов, станков,
перекрытий.Слайд 39 Опыт
Фуко
Тот факт, что Земля вращается вокруг своей оси, сегодня
известен каждому школьнику. Однако не всегда люди были убеждены в этом: обнаружить вращение Земли, находясь на ее поверхности, достаточно трудно. В середине XIX века Жан Бернард Леон Фуко смог провести опыт, который демонстрирует вращение Земли достаточно наглядно. Опыт этот был проведен неоднократно, а публично сам экспериментатор представил его в 1851 году в здании Пантеона в Париже.
)
Леон Фуко
(1819–1868)
Жан Бернард
Слайд 40
Опыт Фуко
Здание Парижского Пантеона в центре венчает
громадный купол, к которому была прикреплена стальная проволока длиной
67 м. К этой проволоке подвесили массивный металлический шар. Масса шара составляла от 25 до 28 кг. Проволока крепилась к куполу таким образом, чтобы получившийся маятник мог качаться в любой плоскости.Маятник совершал колебания над круглым постаментом диаметром 6 м, по краю которого был насыпан валик из песка. При каждом качании маятника острый стержень, укрепленный на шаре снизу, оставлял на валике отметку, сметая с ограждения песок.