- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Дифракция
Содержание
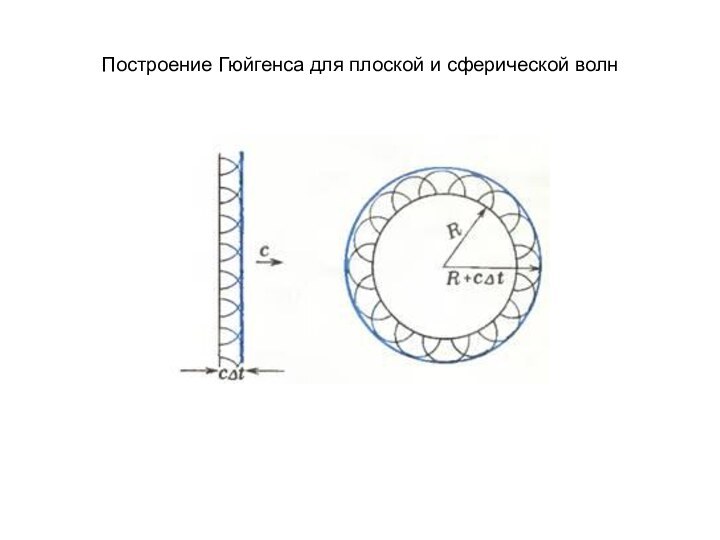
- 2. Построение Гюйгенса для плоской и сферической волн
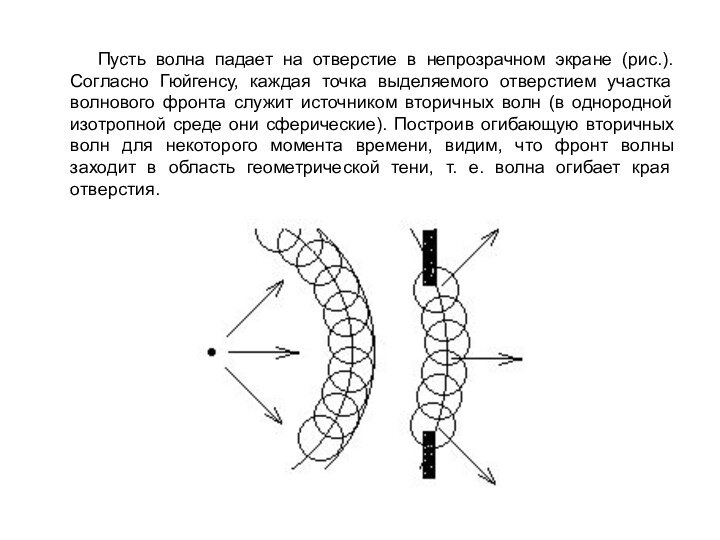
- 3. Пусть волна падает на отверстие
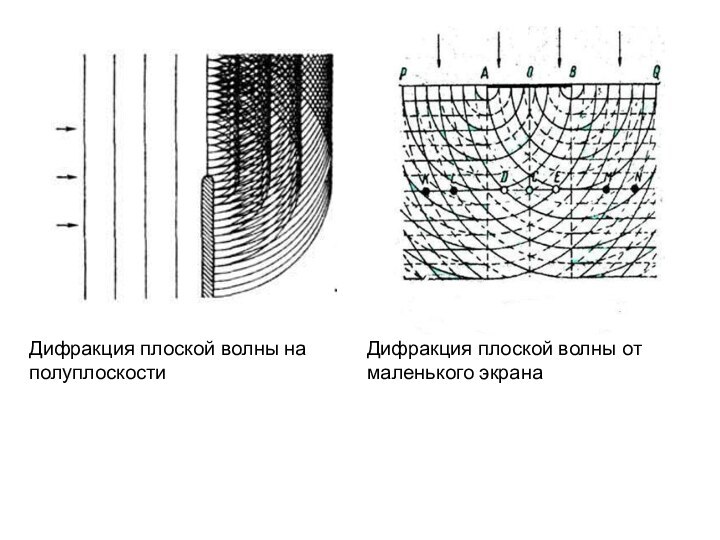
- 4. Дифракция плоской волны на полуплоскостиДифракция плоской волны отмаленького экрана
- 5. Позволяет решить задачу о направлении распространения волнового
- 6. Согласно принципу Гюйгенса — Френеля (1816
- 7. От каждого участка волнового фронта в точку
- 8. Френель исключил возможность возникновения обратных вторичных
- 9. Применим принцип Гюйгенса - Френеля для нахождения
- 10. Расстояние bm от внешнего края m-й зоны
- 11. Волны, приходящие в точку наблюдения от соседних
- 12. Из рис. следует, чтоa - радиус волновой
- 13. После сокращения получимОграничиваясь рассмотрением не слишком больших
- 14. Применив формулу для площади сферического сегмента, получим
- 15. Получим формулу для радиусов зон Френеля.При не слишком больших m высота сегмента hm
- 16. Если положить a=1м, b=1м и λ=0,5мкм
- 17. Фазы колебаний, возбуждаемых соседними зонами, отличаются на
- 18. Полученный результат означает, что амплитуда, создаваемая
- 19. Дифракция Френеля от круглого отверстия Расположим экран
- 20. где m - целое число, то отверстие
- 21. Записанную формулу можно представить в следующем виде:
- 22. При малых m Em ≅ E1. Следовательно,
- 23. Дифракция на диске. Пятно Пуассона.Поместим между точечным
- 24. Диаметр и яркость пятна увеличиваются при уменьшении диаметра диска
- 25. Дифракция Френеля на щели Одномерная дифракция Френеля на
- 26. Дифракция плоских волн или дифракция в параллельных лучах (дифракция Фраунгофера)
- 27. Дифракция плоских волн или дифракция в параллельных
- 28. Щель можно разбить на зоны, имеющие вид
- 29. Если число зон четное: то наблюдается дифракционный
- 30. Одномерная дифракция Фраунгофера на вертикальной щели
- 31. Критерий дифракцииВоспользуемся формулой для радиусов зон Френеля:Выразим
- 32. Если m1 – геометрическая оптика
- 33. На примере дифракции на кольце можно
- 34. Дифракция Фраунгофера на дифракционной решеткеДифракционная решетка —
- 35. Условие минимума для одной щели является также
- 36. Разность хода лучей от соседних щелей равна
- 37. Между дополнительными минимумами располагаются слабые вторичные максимумы.
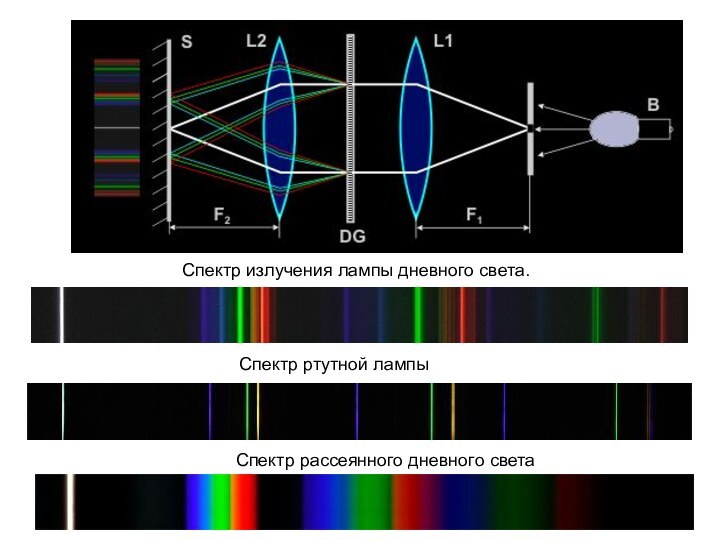
- 38. Исследование спектра света с помощью дифракционной решётки
- 39. Скачать презентацию
- 40. Похожие презентации






















Слайд 5
Позволяет решить задачу о направлении распространения волнового фронта
Достоинство
принципа Гюйгенса
Не позволяет найти амплитуду, а следовательно, и интенсивность
волн, распространяющихся по разным направлениям. Не может объяснить прямолинейное распространение света.
Недостатки:
Френель дополнил принцип Гюйгенса идеей об интерференции вторичных волн.
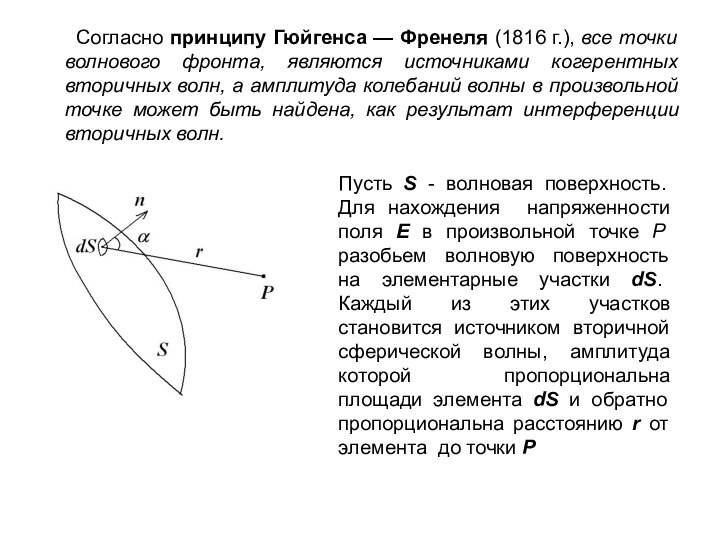
Слайд 6 Согласно принципу Гюйгенса — Френеля (1816 г.),
все точки волнового фронта, являются источниками когерентных вторичных волн,
а амплитуда колебаний волны в произвольной точке может быть найдена, как результат интерференции вторичных волн.Пусть S - волновая поверхность. Для нахождения напряженности поля E в произвольной точке P разобьем волновую поверхность на элементарные участки dS. Каждый из этих участков становится источником вторичной сферической волны, амплитуда которой пропорциональна площади элемента dS и обратно пропорциональна расстоянию r от элемента до точки P
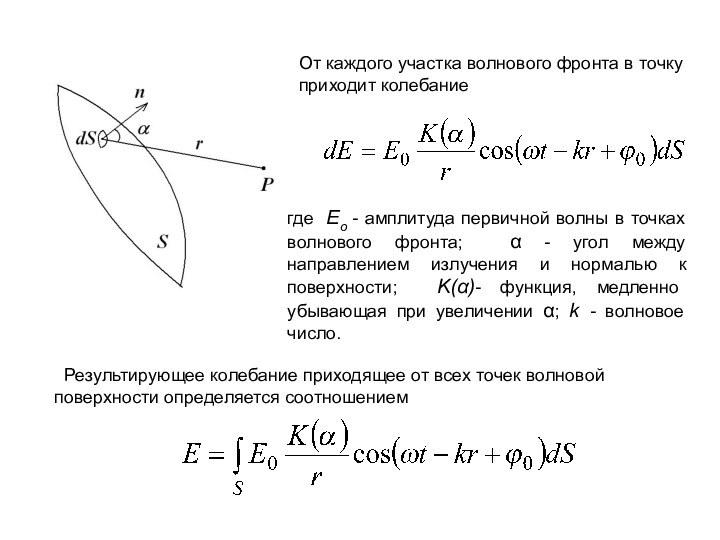
Слайд 7 От каждого участка волнового фронта в точку приходит
колебание
где Eo - амплитуда первичной волны в точках
волнового фронта; α - угол между направлением излучения и нормалью к поверхности; K(α)- функция, медленно убывающая при увеличении α; k - волновое число. Результирующее колебание приходящее от всех точек волновой поверхности определяется соотношением
Слайд 8 Френель исключил возможность возникновения обратных вторичных волн
и предположил, что если между источником и точкой наблюдения
находится непрозрачный экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна нулю, а в отверстии — такая же, как при отсутствии экрана. В общем случае расчет интерференции вторичных волн с использованием записанного интеграла представляет сложную задачу, однако для некоторых симметричных случаев нахождение амплитуды результирующего колебания осуществляется алгебраическим суммированием.
Слайд 9
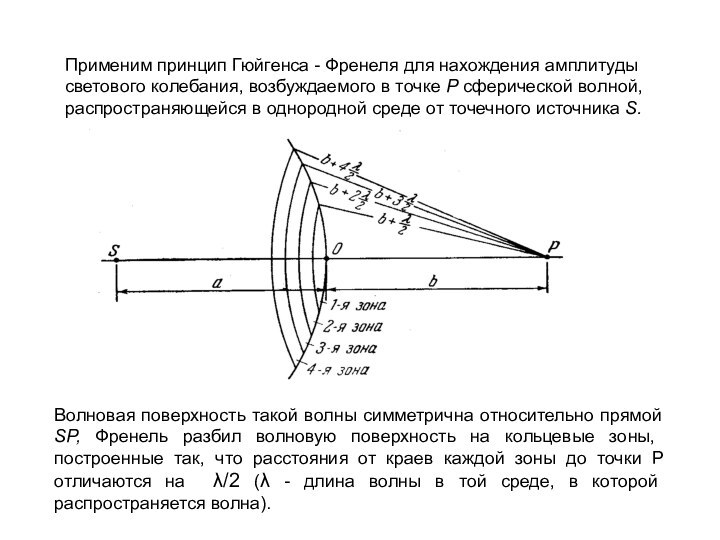
Применим принцип Гюйгенса - Френеля для нахождения амплитуды
светового колебания, возбуждаемого в точке P сферической волной, распространяющейся
в однородной среде от точечного источника S.Волновая поверхность такой волны симметрична относительно прямой SP, Френель разбил волновую поверхность на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки P отличаются на λ/2 (λ - длина волны в той среде, в которой распространяется волна).
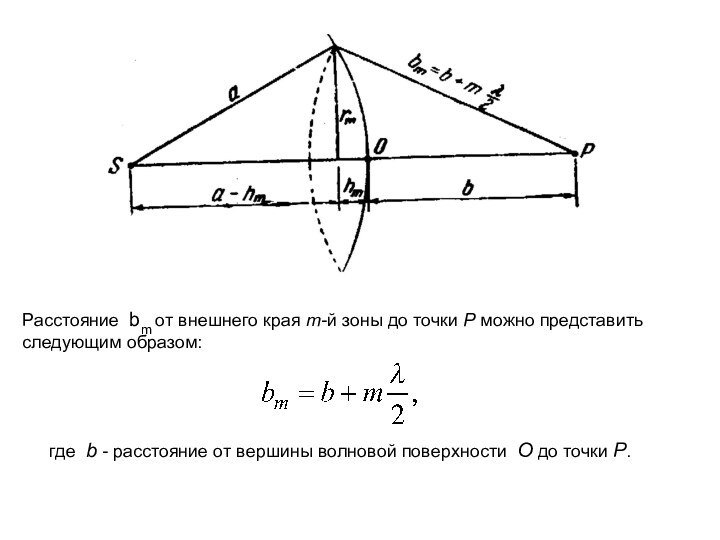
Слайд 10 Расстояние bm от внешнего края m-й зоны до
точки P можно представить следующим образом:
где b - расстояние
от вершины волновой поверхности O до точки P. Слайд 11 Волны, приходящие в точку наблюдения от соседних зон
будут иметь разность фаз
и гасить друг друга.
Для оценки амплитуд колебаний нужно найти величины площадей зон Френеля. Внешняя граница m-й зоны выделяет на волновой поверхности сферический сегмент высоты hm (рис.). Обозначим площадь этого сегмента Sm. Тогда площадь m-й зоны можно представить в виде:где Sm-1 - площадь сферического сегмента, выделяемого внешней границей (m-1)-й зоны.
Слайд 12
Из рис. следует, что
a - радиус волновой поверхности,
rm - радиус внешней границы m-й зоны.
Возведя скобки
в квадрат, получим
Слайд 13
После сокращения получим
Ограничиваясь рассмотрением не слишком больших m,
можно ввиду малости λ пренебречь слагаемым, содержащим λ2. В
этом приближенииПлощадь сферического сегмента равна
R — радиус сферы, h - высота сегмента).
Слайд 14
Применив формулу для площади сферического сегмента, получим
а
площадь m - ой зоны Френеля
Полученное выражение не зависит
от m. Следовательно, при не слишком больших m площади зон Френеля примерно одинаковы.
Слайд 15
Получим формулу для радиусов зон Френеля.
При не слишком
больших m высота сегмента hm
rm2=2ahm. Подставив сюда значение для hm, найдем радиус внешней границы т-й зоны Френеля:
Слайд 16 Если положить a=1м, b=1м и λ=0,5мкм то
для радиуса первой (центральной) зоны получается значение: r1=0,5 мкм.
Радиусы последующих зон возрастают как . Расстояние bm от зоны до точки P медленно растет с по линейному закону. Угол α между нормалью к элементам зоны и направлением на точку P также растет с номером зоны m. Все это приводит к тому, что амплитуда колебания Em, возбуждаемого m-й зоной в точке P, монотонно убывает с ростом m.
Таким образом, амплитуды колебаний, возбуждаемых в точке зонами Френеля, образуют монотонно убывающую последовательность:
Слайд 17 Фазы колебаний, возбуждаемых соседними зонами, отличаются на
π . Поэтому амплитуда результирующего светового колебания в точке
может быть найдена алгебраически:В это выражение все амплитуды от нечетных зон входят с одним знаком, а от четных зон - с другим. Представим это выражение в виде:
Вследствие монотонного убывания Em можно приближенно считать, что
При этом условии выражения, заключенные в круглые скобки, будут равны нулю, и формула упрощается следующим образом:
Слайд 18 Полученный результат означает, что амплитуда, создаваемая в
некоторой точке сферической волновой поверхностью, равна половине амплитуды, создаваемой
одной центральной зоной, т.е. действие всей волновой поверхности эквивалентно половине действия центральной зоны. По произведенной нами оценке центральная зона имеет размеры порядка долей миллиметра. Следовательно, свет от точки к точке распространяется как бы в пределах очень узкого прямого канала, т. е. практически прямолинейно.
Слайд 19
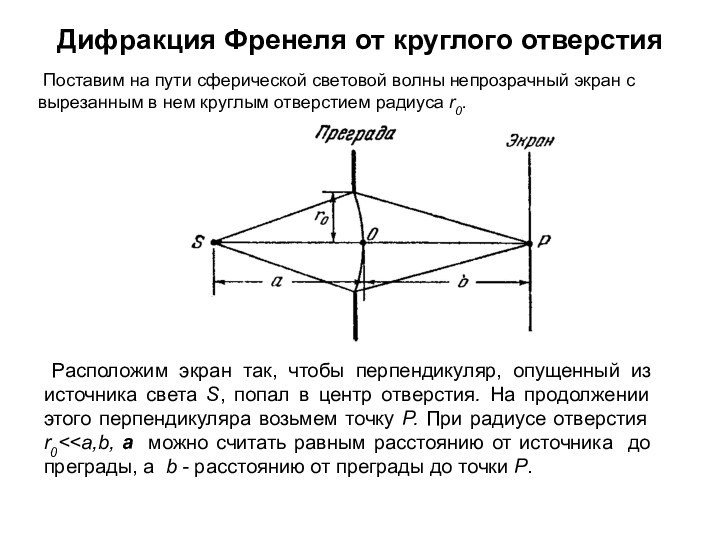
Дифракция Френеля от круглого отверстия
Расположим экран так,
чтобы перпендикуляр, опущенный из источника света S, попал в
центр отверстия. На продолжении этого перпендикуляра возьмем точку P. При радиусе отверстия r0< Поставим на пути сферической световой волны непрозрачный экран с вырезанным в нем круглым отверстием радиуса r0.
Слайд 20 где m - целое число, то отверстие оставит
открытыми ровно m первых зон Френеля, построенных для точки
P.Если расстояния a и b удовлетворяют условию
Выразив m, получим число открытых зон Френеля:
Амплитуда колебания в точке P будет равна:
В этом выражении амплитуда Em берется со знаком плюс, если т нечетное, и со знаком минус, если т четное.
Слайд 21
Записанную формулу можно представить в следующем виде:
Выражения,
заключенные в круглые скобки, можно считать равными нулю. Амплитуды
от двух соседних зон мало отличаются по величине.Поэтому
В результате получится:
где знак «плюс» берется для нечетных m и минус «минус» - для четных.
Слайд 22 При малых m Em ≅ E1. Следовательно, при
нечетном числе зон Френеля амплитуда в точке будет максимальна
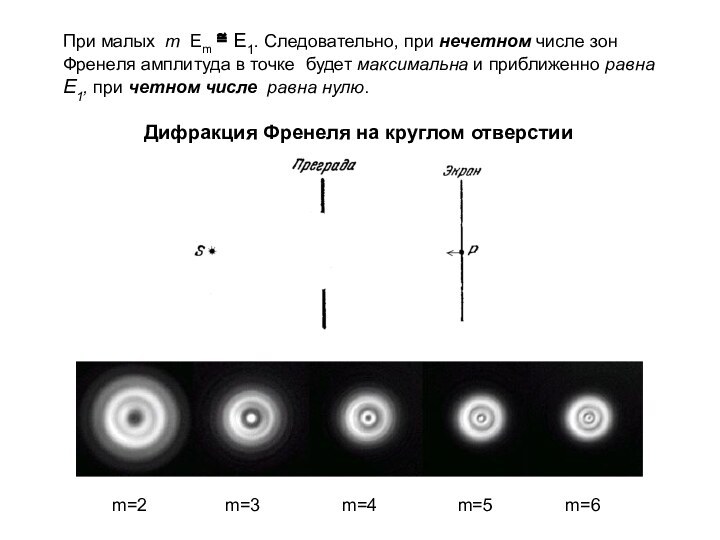
и приближенно равна E1, при четном числе равна нулю.Дифракция Френеля на круглом отверстии
m=2
m=3
m=4
m=5
m=6
Слайд 23
Дифракция на диске. Пятно Пуассона.
Поместим между точечным источником
света S и точкой наблюдения P круглый непрозрачный диск
радиуса r0. Пусть он закрывает т первых зон Френеля. Амплитуда результирующего поля в точке P равна:
Значит интенсивность света в центре геометрической тени отлична от нуля. Таким образом, теория Френеля предсказывает проникновение света в центр геометрической тени диска. Светлое пятно в центре тени получило название «пятно Пуассона».
Слайд 25
Дифракция Френеля на щели
Одномерная дифракция Френеля на вертикальной
щели по мере ее расширения.
Начальная ширина соответствует примерно одной
открытой полуволновой зоне, конечная - пяти открытым зонам.Вертикальный размер картины определяется диаметром пучка, падающего на щель.
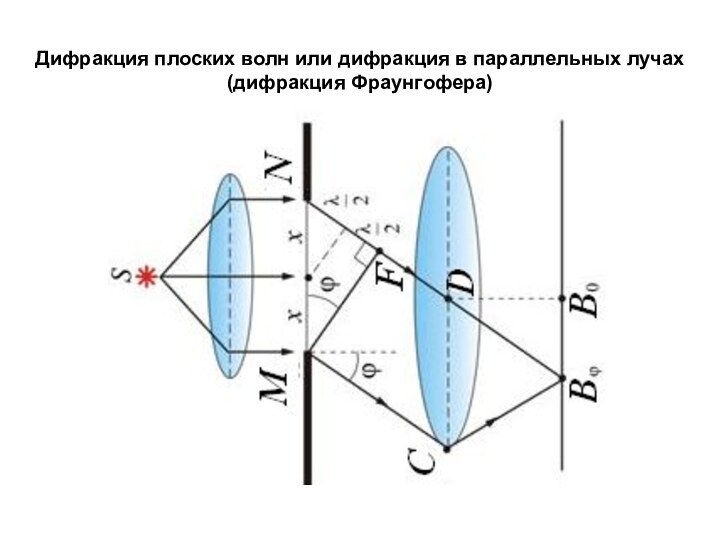
Слайд 27 Дифракция плоских волн или дифракция в параллельных лучах
(дифракция Фраунгофера)
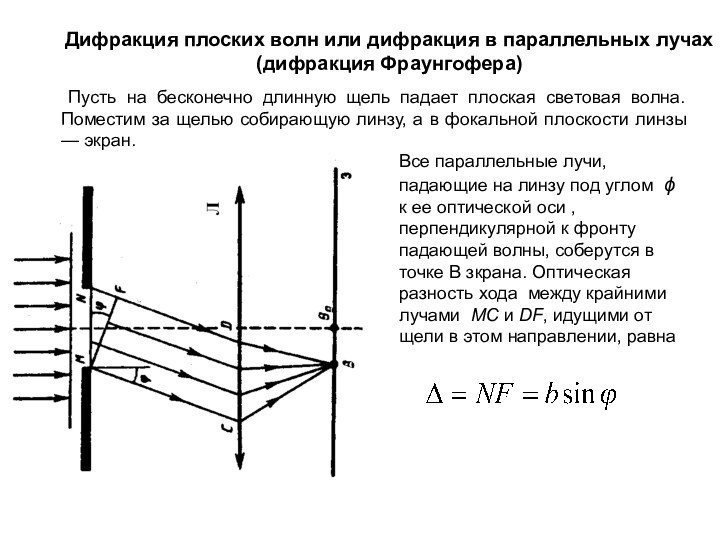
Пусть на бесконечно длинную щель падает плоская
световая волна. Поместим за щелью собирающую линзу, а в фокальной плоскости линзы — экран. Все параллельные лучи, падающие на линзу под углом ϕ к ее оптической оси , перпендикулярной к фронту падающей волны, соберутся в точке B зкрана. Оптическая разность хода между крайними лучами MC и DF, идущими от щели в этом направлении, равна
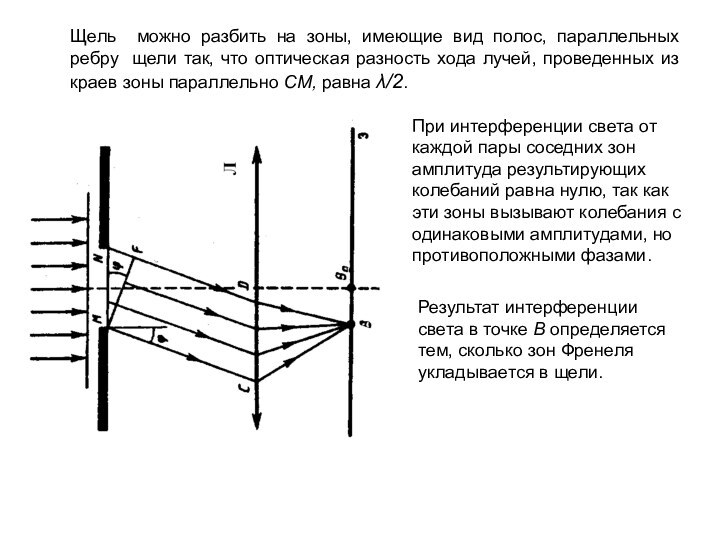
Слайд 28 Щель можно разбить на зоны, имеющие вид полос,
параллельных ребру щели так, что оптическая разность хода лучей,
проведенных из краев зоны параллельно СМ, равна λ/2.При интерференции света от каждой пары соседних зон амплитуда результирующих колебаний равна нулю, так как эти зоны вызывают колебания с одинаковыми амплитудами, но противоположными фазами.
Результат интерференции света в точке B определяется тем, сколько зон Френеля укладывается в щели.
Слайд 29
Если число зон четное:
то наблюдается дифракционный минимум.
Если число зон нечетное:
то наблюдается дифракционный максимум.
Величина m
называется порядком дифракционного максимума. В направлении ϕ=0 наблюдается самый интенсивный центральный максимум нулевого порядка.
Слайд 30 Одномерная дифракция Фраунгофера на вертикальной щели по
мере ее расширения слева направо.
Размер области дифракционного расплывания
обратно пропорционален ширине щели.
Слайд 31
Критерий дифракции
Воспользуемся формулой для радиусов зон Френеля:
Выразим m:
Пусть а→∞ (случай плоской световой волны), тогда
Воспользуемся этим
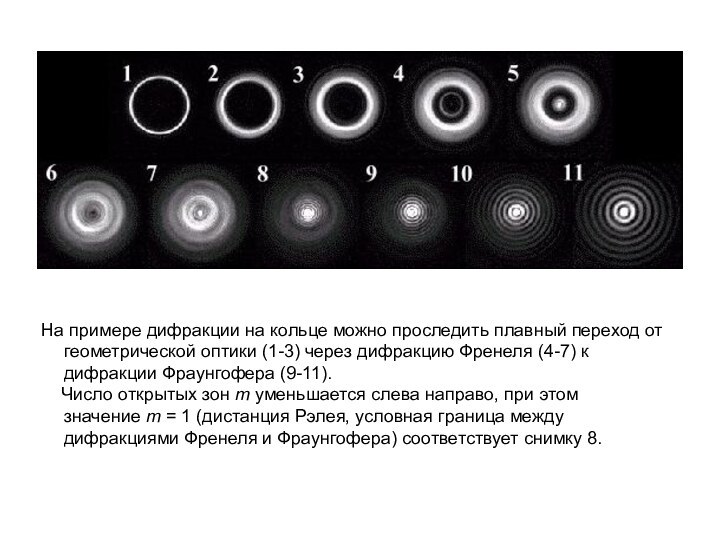
соотношением, как критерием вида дифракции, заменив rm на h (характерный размер отверстия).Слайд 33 На примере дифракции на кольце можно проследить
плавный переход от геометрической оптики (1-3) через дифракцию Френеля
(4-7) к дифракции Фраунгофера (9-11).Число открытых зон m уменьшается слева направо, при этом значение m = 1 (дистанция Рэлея, условная граница между дифракциями Френеля и Фраунгофера) соответствует снимку 8.
Слайд 34
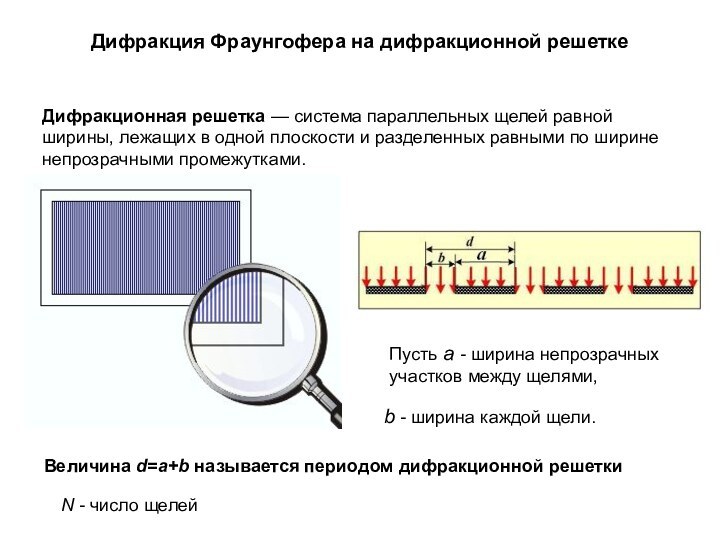
Дифракция Фраунгофера на дифракционной решетке
Дифракционная решетка — система
параллельных щелей равной ширины, лежащих в одной плоскости и
разделенных равными по ширине непрозрачными промежутками.b - ширина каждой щели.
Пусть a - ширина непрозрачных участков между щелями,
Величина d=a+b называется периодом дифракционной решетки
N - число щелей
Слайд 35 Условие минимума для одной щели является также условием
минимума для решетки
(1)
Пусть на дифракционную решётку падает плоская монохроматическая
волна.
Слайд 36
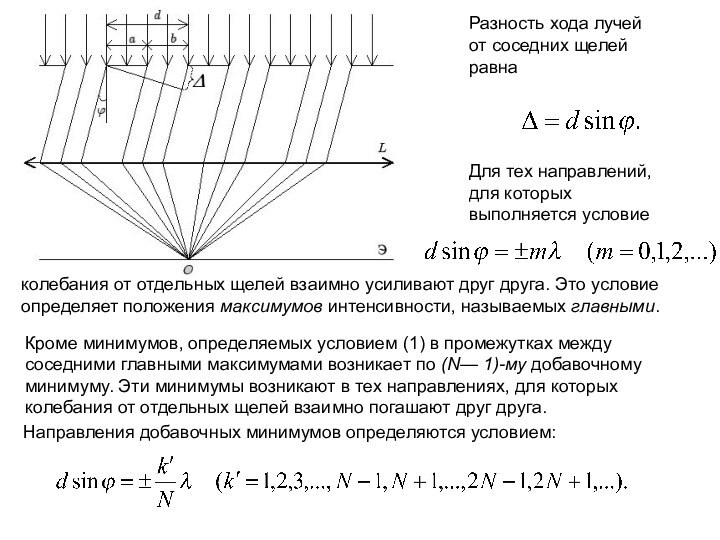
Разность хода лучей от соседних щелей равна
Для
тех направлений, для которых выполняется условие
колебания от отдельных
щелей взаимно усиливают друг друга. Это условие определяет положения максимумов интенсивности, называемых главными. Кроме минимумов, определяемых условием (1) в промежутках между соседними главными максимумами возникает по (N— 1)-му добавочному минимуму. Эти минимумы возникают в тех направлениях, для которых
колебания от отдельных щелей взаимно погашают друг друга.
Направления добавочных минимумов определяются условием:
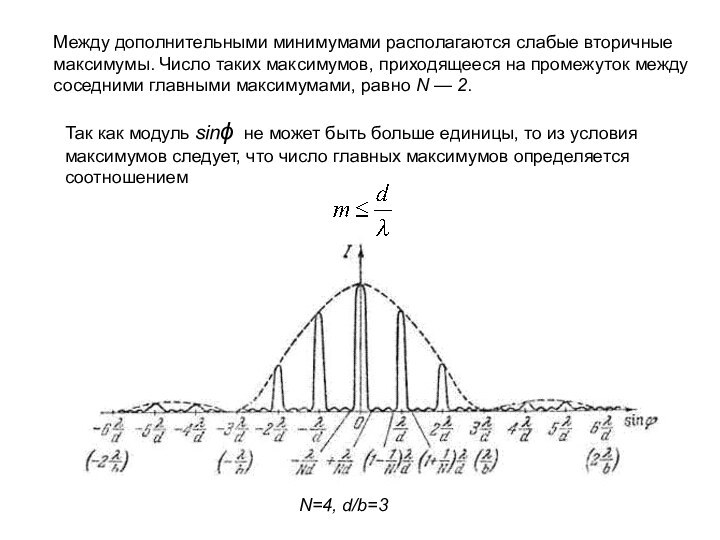
Слайд 37 Между дополнительными минимумами располагаются слабые вторичные максимумы. Число
таких максимумов, приходящееся на промежуток между соседними главными максимумами,
равно N — 2.Так как модуль sinϕ не может быть больше единицы, то из условия максимумов следует, что число главных максимумов определяется соотношением
N=4, d/b=3