- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Вероятностные явления в возмущенных динамических системах
Содержание
- 2. Вероятностные явления связаны с неперестановочностью пределов:d- неточность знания начальных условийT- время движенияВозмущеннаясистема=Интегрируемая системаВозмущение
- 3. Темы:Вероятностное рассеяние при переходах через сепаратрисуСкачки адиабатического
- 4. I. Вероятностное рассеяние при переходах через сепаратрисуПример (В.И.Арнольд, 1963)V12q+ малое трениеФазовые портреты: приприq12C(1)(2)
- 6. Вероятностный подход:И.М.Лифшиц, А.А.Слуцкин, В.М.Набутовский (1961) - движение
- 7. qqПример: маятникФазовый портрет приВероятность захвата в колебательный режим (из режима прямого вращения):, если, если
- 8. Исследование приливного механизма захвата Меркурия в резонанс
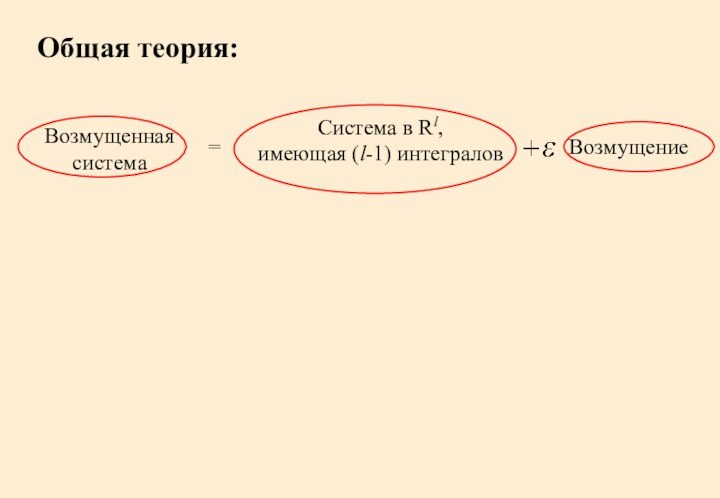
- 10. Общая теория:Возмущенная система=Система в Rl,имеющая (l-1) интеграловВозмущение
- 12. Скачок адиабатического инварианта при переходе маятника через
- 13. Остров устойчивости:Суммарная мера островов устойчивости ~1 (А.Н., В.В.Сидоренко, Д.В.Трещев, 1997)
- 15. Влияние резонансовВблизи резонанса (k, w(I)) = 0
- 16. Пример: движение заряженных частиц в однородном магнитном
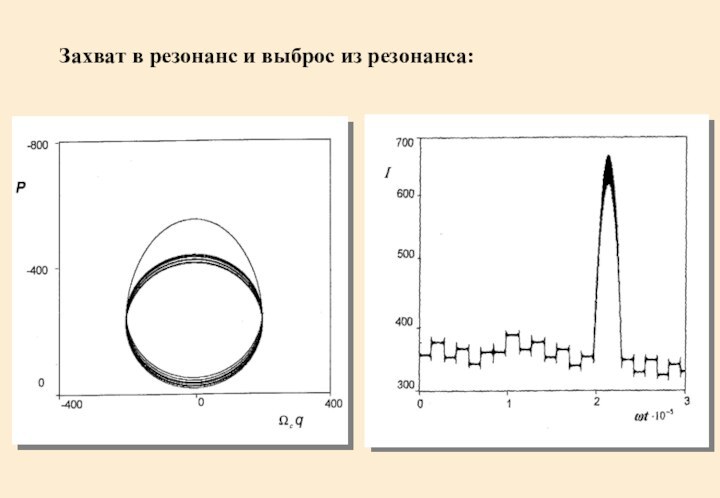
- 17. Захват в резонанс и выброс из резонанса:
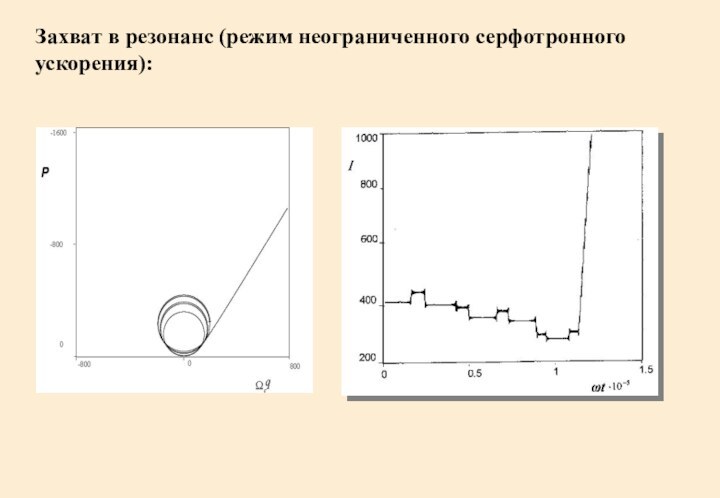
- 18. Захват в резонанс (режим неограниченного серфотронного ускорения):
- 19. Рассеяние на резонансе:
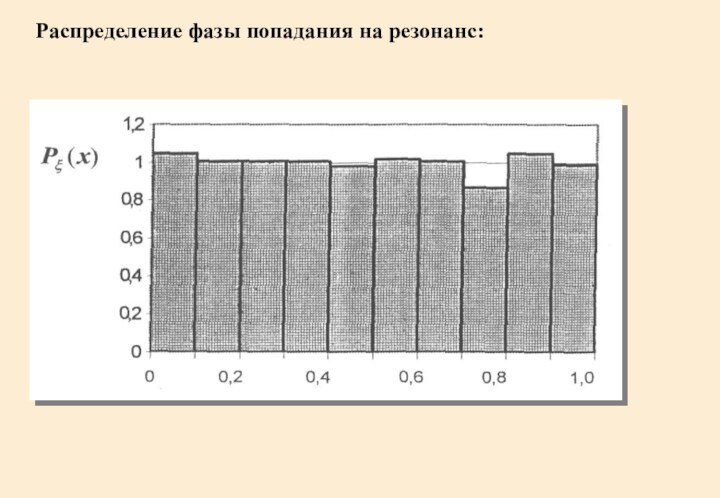
- 20. Распределение фазы попадания на резонанс:
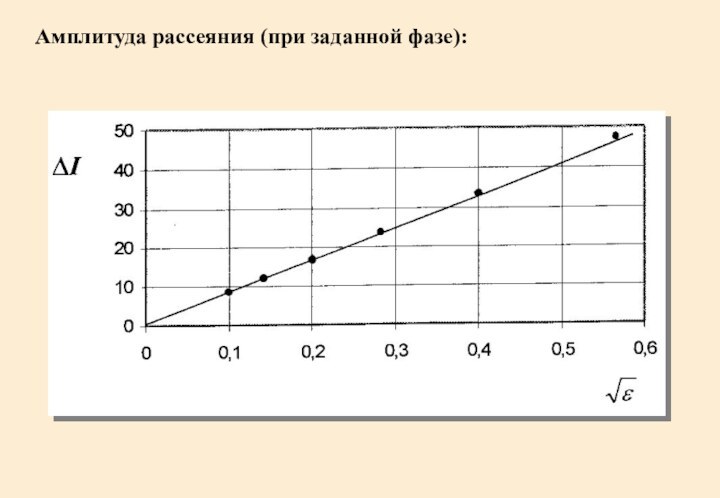
- 21. Амплитуда рассеяния (при заданной фазе):
- 22. Скачать презентацию
- 23. Похожие презентации
Вероятностные явления связаны с неперестановочностью пределов:d- неточность знания начальных условийT- время движенияВозмущеннаясистема=Интегрируемая системаВозмущение










Слайд 2
Вероятностные явления связаны с неперестановочностью пределов:
d- неточность знания
начальных условий
Слайд 3
Темы:
Вероятностное рассеяние при переходах через сепаратрису
Скачки адиабатического инварианта
при переходах через сепаратрису
Рассеяние на резонансах, захват в резонанс
Слайд 4
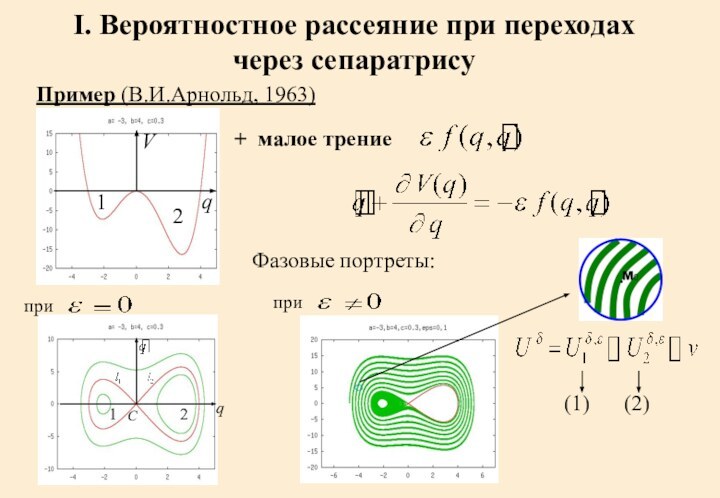
I. Вероятностное рассеяние при переходах через сепаратрису
Пример (В.И.Арнольд,
1963)
V
1
2
q
+ малое трение
Фазовые портреты:
при
при
q
1
2
C
(1)
(2)
Слайд 6
Вероятностный подход:
И.М.Лифшиц, А.А.Слуцкин, В.М.Набутовский (1961) - движение заряженных
квазичастиц
В.И.Арнольд (1963) - математическое определение вероятности
P.Goldreich, S.Peale (1966) -
приливная эволюция вращения планетА.В.Гуревич, Е.Е.Цидилина (1979) - распространение радиоволн в ионосферных волноводных каналах
G.Wolansky(1990), М.Брин, М.Фрейдлин (1999) - другое определение вероятности (+малая случайная сила) - «ответ» тот же
Слайд 7
q
q
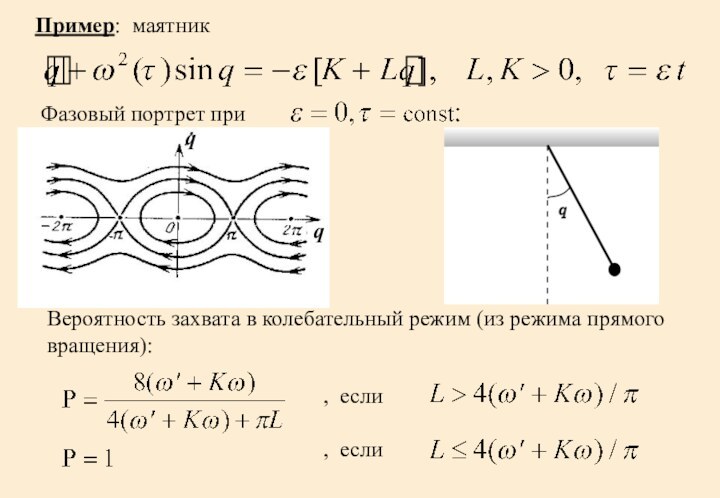
Пример: маятник
Фазовый портрет при
Вероятность захвата в колебательный режим
(из режима прямого вращения):
, если
, если
Слайд 8 Исследование приливного механизма захвата Меркурия в резонанс приводит
к задаче о захвате маятника в режим колебаний (P.Goldreich,
S.Peale, 1966 ):S
M
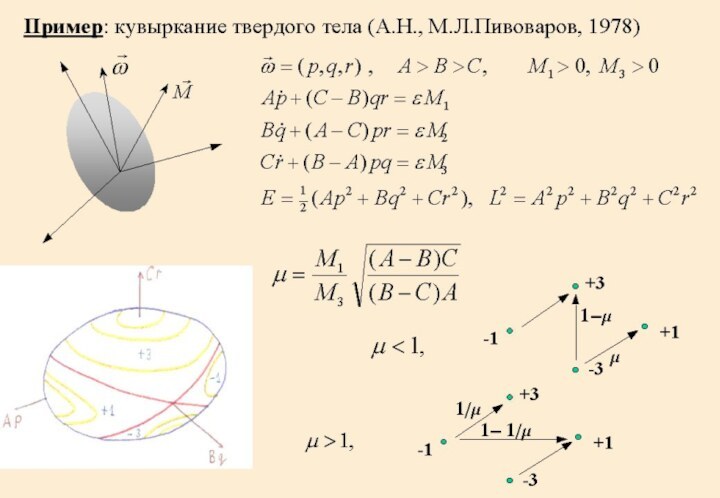
Слайд 12 Скачок адиабатического инварианта при переходе маятника через сепаратрису
(А.В.Тимофеев, 1978) :
x - квазислучайная величина, распределенная равномерно на
(0,1)Общая формула: А.Н. (1986); J.Cary, D.Escande, J.Tennyson (1986).
Примеры:
Происхождение люка Кирквуда на резонансе 3:1 (J.Wisdom, 1985)
Движение заряженных частиц в хвосте магнитосферы Земли (Й.Бюхнер, Л.М.Зеленый, 1989)
Слайд 13
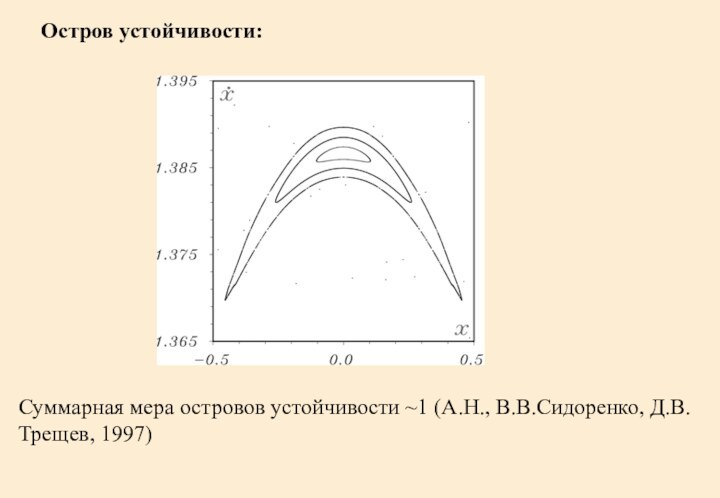
Остров устойчивости:
Суммарная мера островов устойчивости ~1 (А.Н., В.В.Сидоренко,
Д.В.Трещев, 1997)
Слайд 15
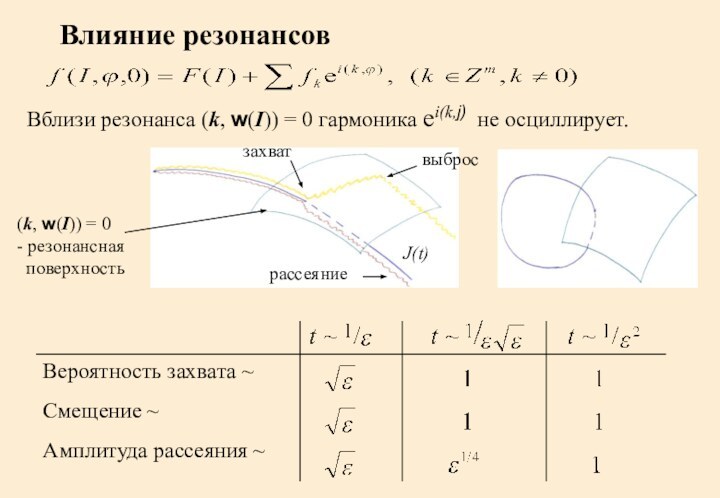
Влияние резонансов
Вблизи резонанса (k, w(I)) = 0 гармоника
ei(k,j) не осциллирует.
захват
(k, w(I)) = 0
- резонансная
поверхностьвыброс
рассеяние
J(t)
Вероятность захвата ~
Смещение ~
Амплитуда рассеяния ~
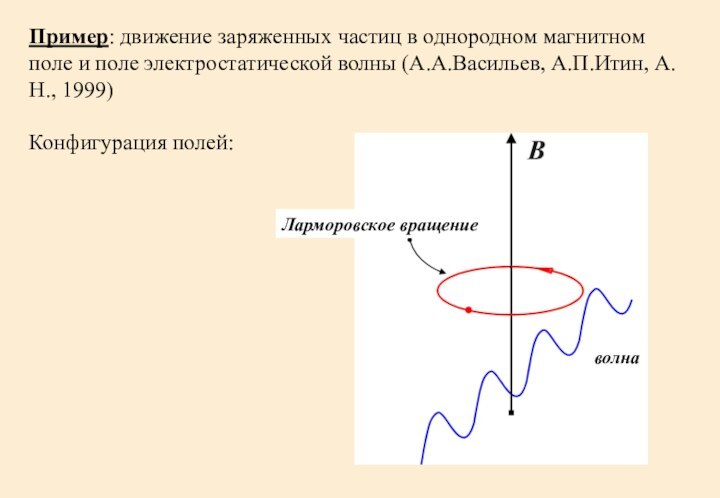
Слайд 16 Пример: движение заряженных частиц в однородном магнитном поле
и поле электростатической волны (А.А.Васильев, А.П.Итин, А.Н., 1999)
Конфигурация полей:
Ларморовское
вращениеволна