Презентация на тему Динамика материальной системы

материальной системы в ее абсолютном движении (T) складывается из

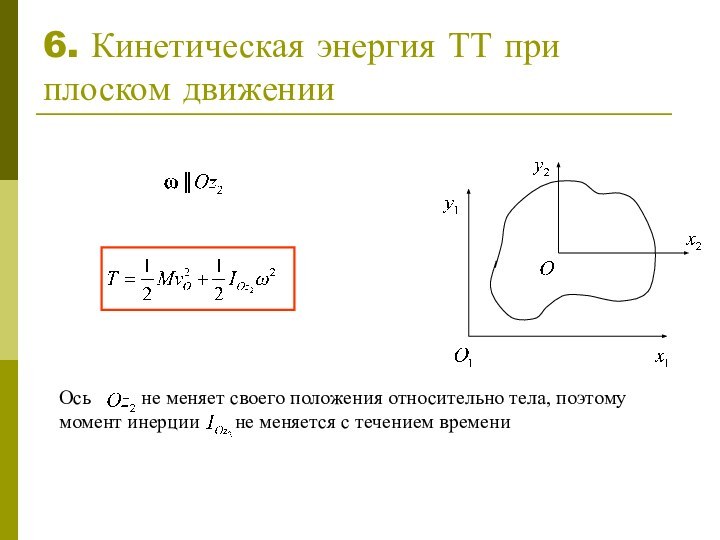
кинетической энергии TO центра масс, в предположении, что в нем сосредоточена масса всей системы, и кинетической энергии Tотн системы в ее движении относительно поступательно перемещающихся в инерциальном пространстве вместе с центром масс осей.

Кинетической энергией материальной системы называется сумма кинетических энергий входящих в нее точек

При вычислении кинетической энергии системы полезна теорема Кенига

относительно инерциальных осей (1) вместе с центром О масс

системы.

движущегося поступательно, равна половине произведения массы тела на квадрат

его скорости

ТТ, вращающегося вокруг неподвижной оси, равна половине произведения момента

инерции тела относительно оси вращения на квадрат угловой скорости тела

складывается из кинетической энергии поступательного движения вместе с центром

масс и кинетической энергии в его вращении относительно центра масс

Теорема Кенига

Кинематика: движение тела относительно поступательно перемещающихся осей (2) представляет собой вращение с угловой скоростью

В общем случае переменная величина т.к. ось вращения изменяет свое положение

лежит на горизонтальной плос-кости. Каток обмотан тросом, перекинутым через

блок Б радиуса r. К свободному концу троса при-креплен груз Г массы m3. При опускании груза со скоростью v трос, разматываясь, приводит в качение без скольжения каток. Определить кинетическую энергию системы, если момент инерции блока Б относительно оси вращения равен I2

Скорость точки касания блока с тросом равна скорости v груза Г.

об изменении кинетической энергии : дифференциал кинетической энергии системы

равен сумме элементарных работ всех действующих на систему внешних и внутренних сил.

Интегральная форма теоремы: изменение кинетической энергии системы при перемещении ее из какой-то начальной конфигурации в данную равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил

равна весу всей системы, умноженному на вертикальное перемещение ее

центра тяжести

внутренних сил абсолютно твердого тела на любом его перемещении

равна нулю

Кинематика

работа силы, приложенной к твердому телу, вращающемуся вокруг неподвижной

оси, равна моменту этой силы относительно оси вращения, умноженному на дифференциал угла поворота тела

Мощность:

внутренних сил трения скольжения двух
сочлененных тел равна взятому

со знаком минус произведению модуля
силы трения на модуль относительной скорости.

Скорость A относительно B

(внутренняя энергия)

точку #1 действуют потенциальные внешние силы
На точку #2 действуют

потенциальные внешние силы

На точку #n действуют потенциальные внешние силы

…

…

сил
Допустим, что внутренние и внешние силы, работа которых отлична

от нуля, потенциальны (нулю может равняться работа идеальных связей).

E-полная механическая энергия системы

Систему, для которой имеет место интеграл энергии, называют консервативной.

интеграл энергии

Ui-внутренняя энергия

по наклонной плоскости. Начальная скорость равна нулю. Найти скорость

центра масс цилиндра в момент времени когда он опустился на величину h.

Если это тело спускается не вращаясь, имеем

Следовательно, вращение уменьшает скорость

силы тяжести опускается из состояния покоя вниз. Определить скорость

v груза Г при опускании его на высоту h. Трением качения катка и трением на оси блока пренебречь.

Связи идеальны. Внутренняя энергия равна нулю

m1 лежащему на гладкой горизонтальной плоскости, прикреплен шарнирно в

точке А однородный стержень АВ, имеющий массу m2 и длину l. Система начинает движение из состояния покоя в момент, когда стержень отклонен до горизонтального положения АВ0. Пренебрегая трением в оси А, найти скорость v бруса в тот момент, когда стержень проходит через вертикаль.

скорость С относительно А

Сохранение энергии

Сохранение импульса