Слайд 3
План лекции
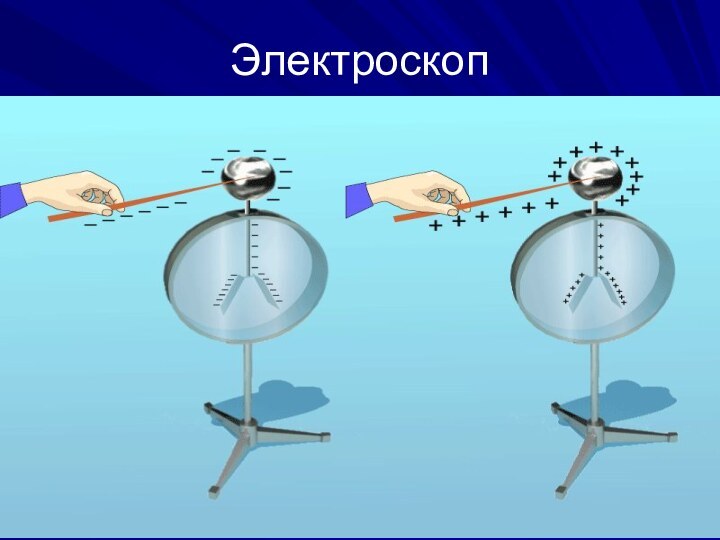
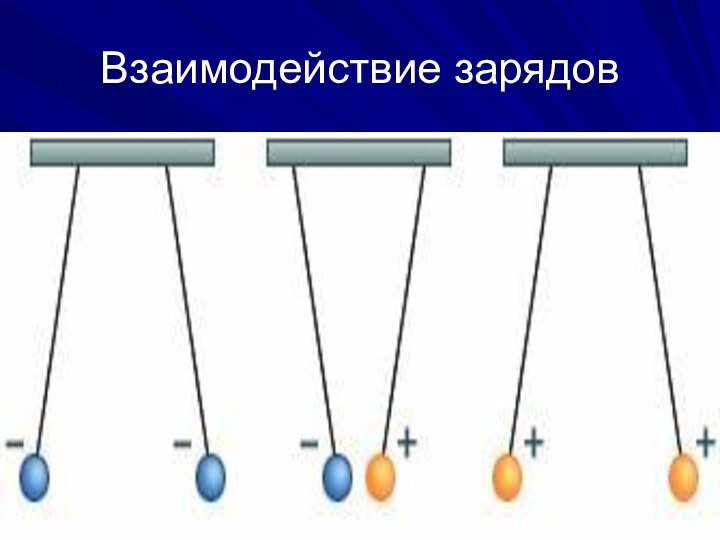
Электрический заряд и его свойства
Закон сохранения заряда.
Закон Кулона.
Напряжённость электростатического поля.
Линии напряжённости электростатического поля. Поток вектора
напряжённости.
Принципы суперпозиции. Поле диполя.
Теорема Гаусса для электростатического поля в вакууме.
Циркуляция вектора напряжённости электростатического поля.
Потенциал электростатического поля.
Слайд 6
Закон сохранения заряда
Алгебраическая сумма электрических зарядов любой замкнутой
системы остаётся неизменной, какие бы процессы ни происходили внутри
данной системы.
Замкнутая система – система, не обменивающая зарядами с внешними телами
Слайд 11
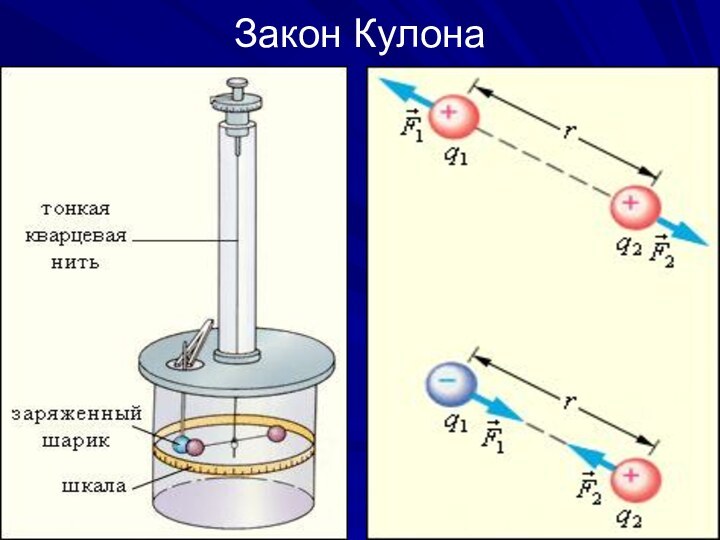
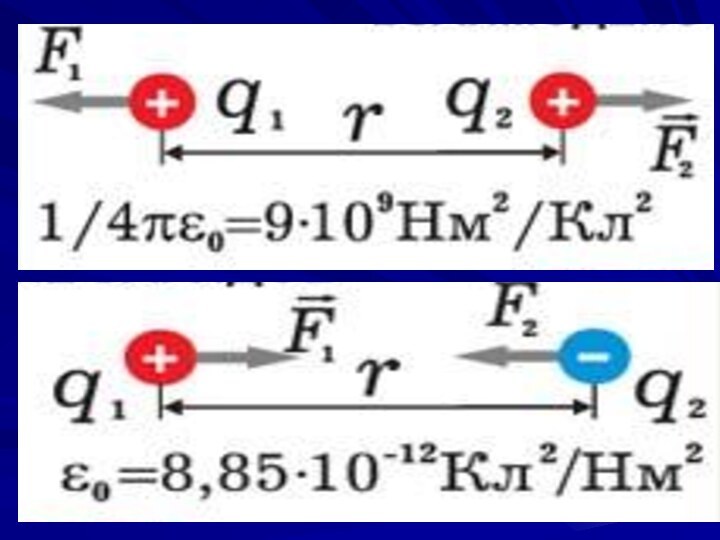
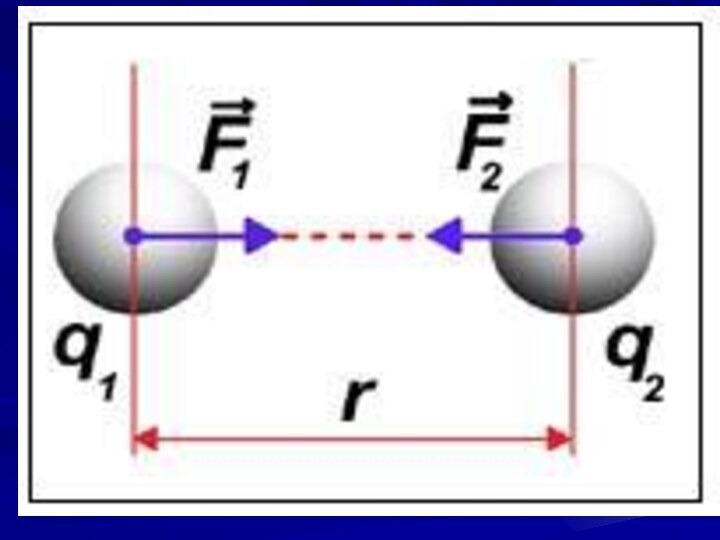
Закон Кулона
Сила взаимодействия между неподвижными точечными зарядами, находящимися
в вакууме, пропорциональна зарядам и и обратно пропорциональна квадрату расстояния
между ними:
Слайд 15
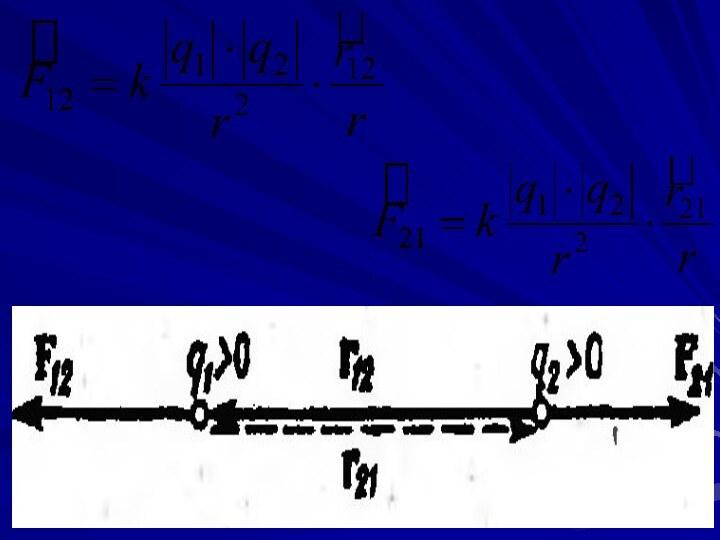
Кулоновская сила
Сила направлена по прямой, соединяющей взаимодействующие заряды,
т.е. является центральной.
В случае разноимённых зарядов - соответствует притяжению.
В
случае одноимённых зарядов - соответствует отталкиванию.
Эта сила называется кулоновской силой.
Слайд 16
Распределение электрических зарядов
Слайд 17
Линейная плотность электрических зарядов
Слайд 18
Поверхностная плотность электрических зарядов
Слайд 19
Объемная плотность электрических зарядов
Слайд 20
Напряженность электрического поля
Слайд 21
Электростатическое поле
Напряжённость электростатического поля – физическая величина, определяемая
силой, действующей на единичный положительный заряд, помещённый в данную
точку поля:
Напряжённость электростатического поля – силовая векторная характеристика электростатического поля.
Слайд 22
Напряженность поля
точечного заряда
Слайд 23
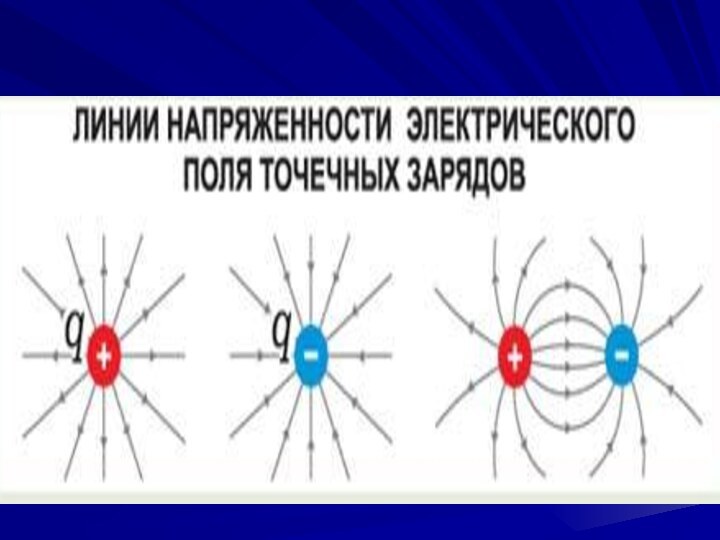
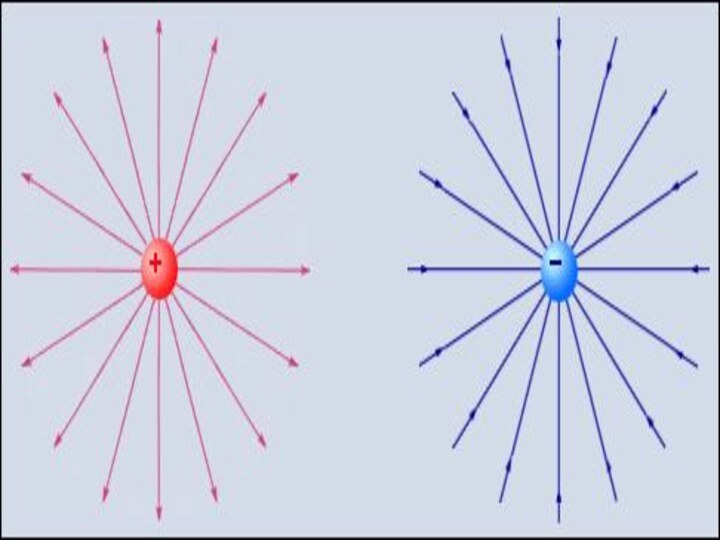
Вектор напряженности во всех точках поля направлен
радиально от заряда, если он положителен,
и радиально к
заряду, если отрицателен
Слайд 24
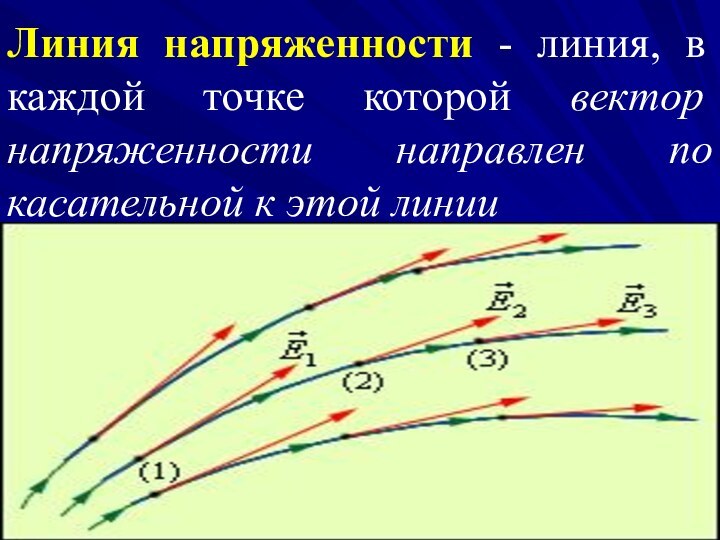
Линия напряженности - линия, в каждой точке которой
вектор напряженности направлен по касательной к этой линии
Слайд 28
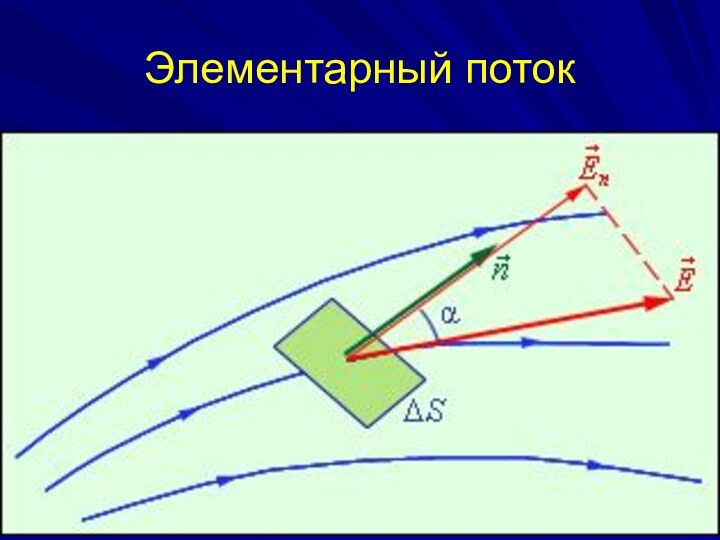
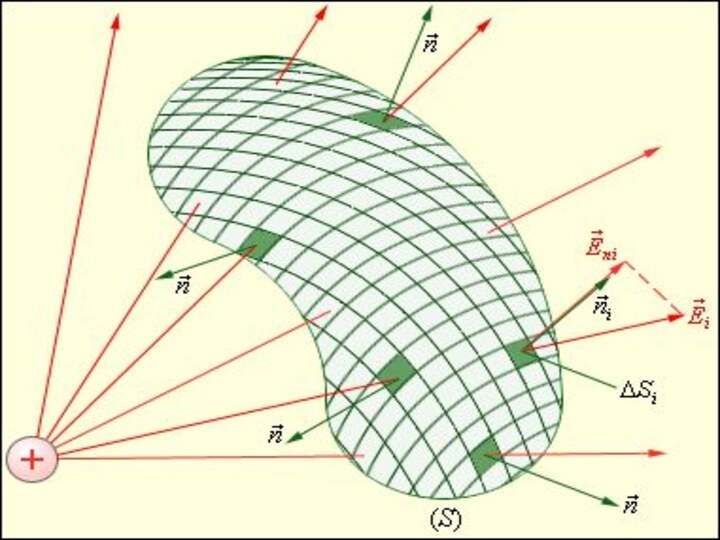
Поток вектора напряженности электрического поля.
Поток вектора
электрического поля
через поверхность S измеряется
числом силовых линий пронизывающих данную поверхность.
Слайд 29
Поток вектора напряжённости электростатического поля
Слайд 31
Поток вектора напряженности через произвольную поверхность, окружающую заряд
Слайд 32
.
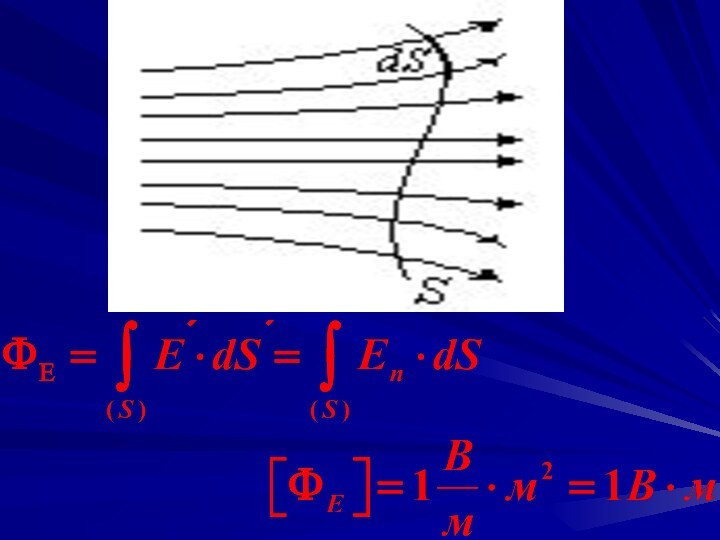
В случае однородного поля, перпендикуляр-ного к плоской повер-хности
число линий, пронизывающих 1 м2
равно Е , а через всю поверхность S┴ по-ток вектора напря-женности будет равен
Слайд 34
Введем понятие вектора площади
сонаправленного с единичным вектором
нормали к
поверхности S , а по модулю
равного площади этой поверхности
Тогда поток через поверхность будет равен
Слайд 35
Произвольная поверхность
неоднородного поля
Слайд 37
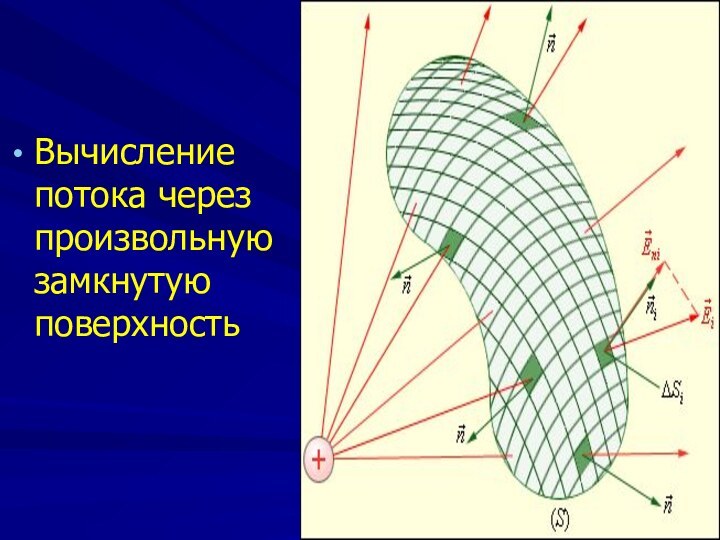
Вычисление потока через произвольную
замкнутую поверхность
Слайд 39
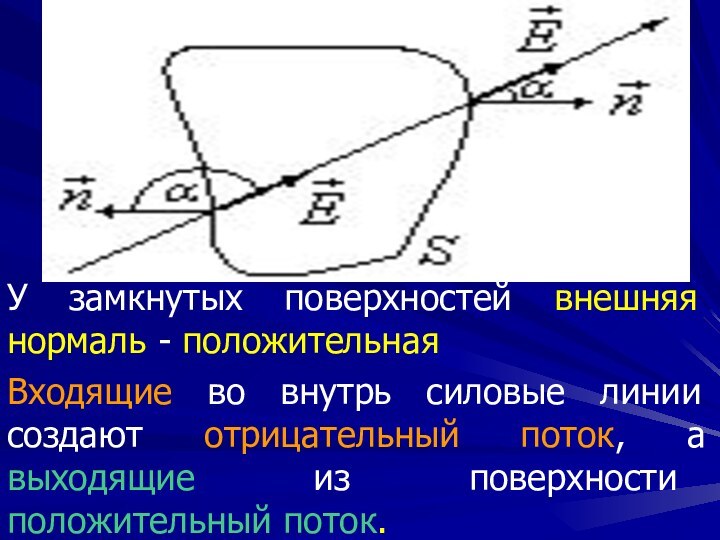
У замкнутых поверхностей внешняя нормаль - положительная
Входящие во
внутрь силовые линии создают отрицательный поток, а выходящие из
поверхности положительный поток.
Слайд 40
Поток вектора напряженности
сквозь сферическую поверхность радиуса R
Слайд 41
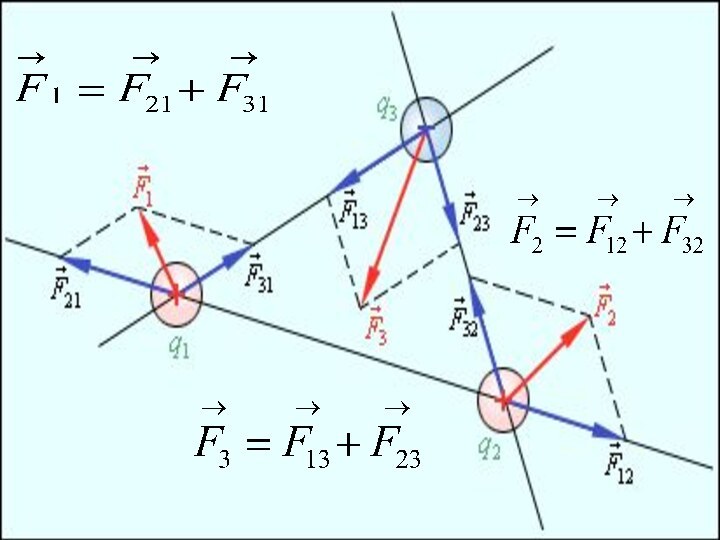
Принцип суперпозиции электростатических сил
Слайд 42
Результирующая сила, действующая на пробный заряд в любой
точке поля равна геометрической сумме сил, приложенных к этому
заряду со стороны неподвижных точечных зарядов
Слайд 44
Принцип суперпозиции полей
напряженность результирующего поля, создаваемого системой зарядов,
равна геометрической сумме напряженностей полей, создаваемых в данной точке
каждым из зарядов в отдельности
Слайд 45
Напряженность электростатического поля
Слайд 48
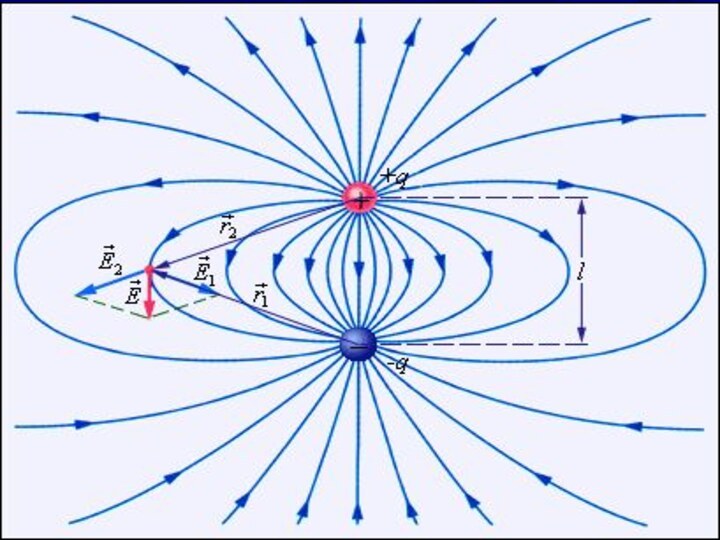
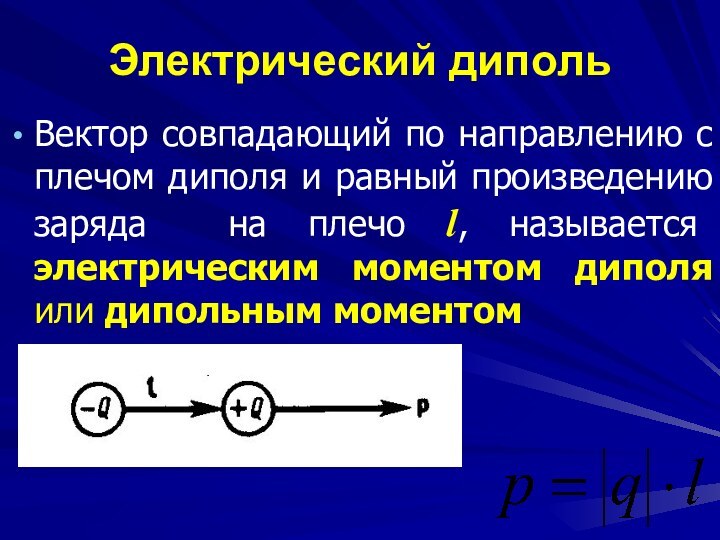
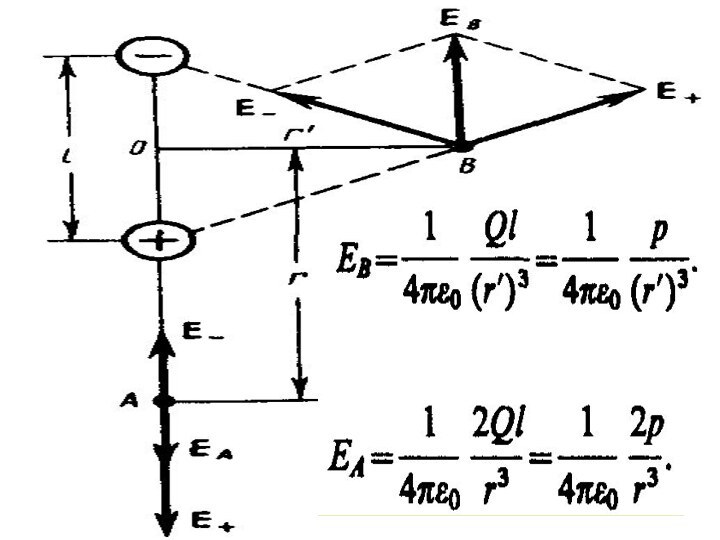
Электрический диполь
система двух равных по модулю разноименных
точечных зарядов, расстояние l между которыми значительно меньше расстояния
до рассматриваемых точек поля.
Слайд 49
Электрический диполь
Вектор, направленный по оси диполя (прямой,
проходящей через оба заряда) от отрицательного заряда к положительному
и равный расстоянию между ними, называется плечом диполя l.
Слайд 50
Электрический диполь
Вектор совпадающий по направлению с плечом
диполя и равный произведению заряда на плечо l, называется
электрическим моментом диполя или дипольным моментом
Слайд 52
Непрерывное распределение системы зарядов в пространстве
Напряженность поля этой
системы в вакууме, согласно принципу суперпозиции полей
Слайд 53
Электростатическое поле точечного заряда – центральное и поэтому
потенциальное.
На точечный заряд в этом поле действует сила,
работа этой силы на любой замкнутой траектории равна нулю
Слайд 54
Циркуляция вектора напряженности вдоль замкнутого контура
Циркуляция вектора напряженности
электрического поля точечного заряда вдоль произвольного замкнутого контура, проведенного
в поле равна нулю.
Слайд 55
Напряженность электрического поля
произвольной системы точечных зарядов
Слайд 56
Это соотношение подтверждает то, что любое электростатическое поле
потенциально
Слайд 57
Циркуляция вектора напряжённости
Интеграл называется
циркуляцией вектора напряжённости.
Теорема о
циркуляции вектора
Силовое поле, обладающее таким свойством, называется потенциальным.
Слайд 58
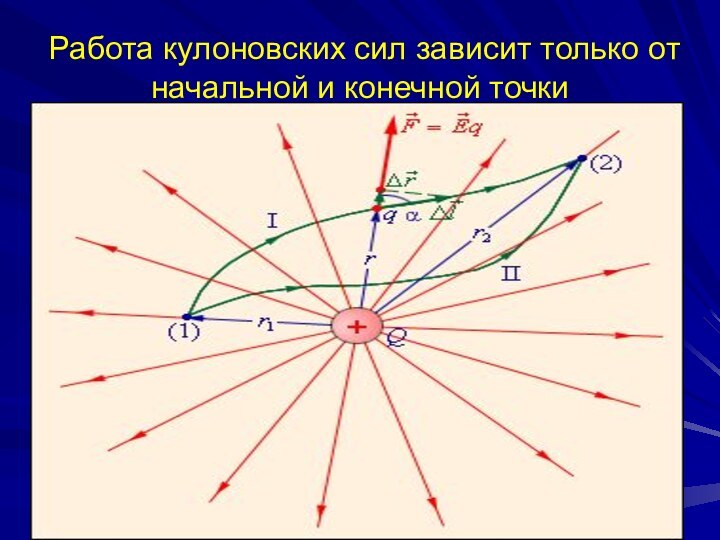
Работа перемещения заряда в поле
Работа при перемещении заряда
из точки 1 в точку 2:
не
зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек.
Электростатическое поле точечного заряда является потенциальным, а электростатические силы – консервативными.
Слайд 59
Работа перемещения заряда
в поле
Работа перемещения заряда во
внешнем электростатическом поле по любому замкнутому контуру
будет равна:
Слайд 60
Работа кулоновских сил зависит только от начальной и
конечной точки
Уравнения электростатики в вакууме
Слайд 61
Работа, совершаемая силами электростатического поля при малом перемещении
точечного заряда в этом поле, равна убыли потенциальной энергии
заряда в рассматриваемом поле
Слайд 62
Для поля системы из n точечных зарядов
Слайд 63
При непрерывном распределении зарядов в пространстве, потенциальная энергия
заряда в поле равна
Слайд 64
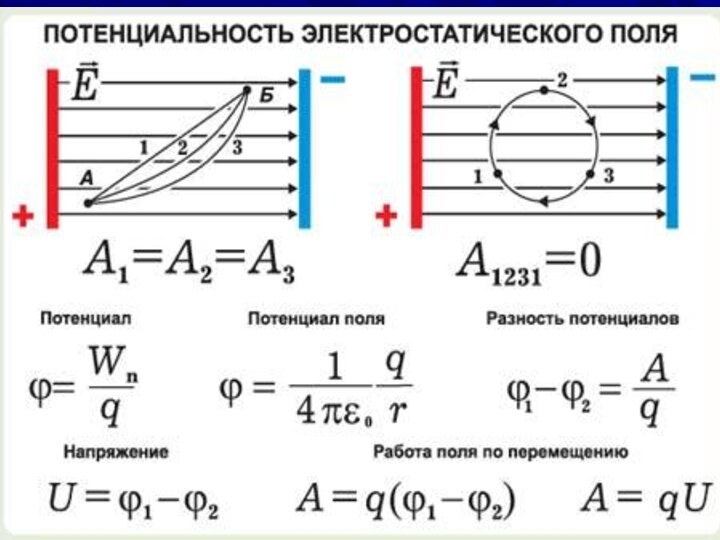
Потенциал электростатического поля
Слайд 65
Потенциалом электростатического поля называется физическая величина, равная отношению
потенциальной энергии пробного точечного электрического заряда, помещенного в рассматриваемую
точку поля, к этому заряду
Слайд 66
Принцип суперпозиции электростатических полей
Если поле создаётся несколькими зарядами,
то потенциал поля системы зарядов равен алгебраической сумме потенциалов
полей всех этих зарядов
Слайд 67
При наложении электростатических полей их потенциалы складываются алгебраически
Слайд 68
Работа перемещения заряда в поле
Работа сил электростатического поля
при перемещении точечного заряда из точки 1 в точку
2
т.е., равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках.
Слайд 69
Разность потенциалов
Разность потенциалов двух точек 1 и 2
в электростатическом поле определяется работой, совершаемой силами поля, при
перемещении единичного положительного заряда из точки 1 в точку 2.
Слайд 71
Потенциал
Потенциал – физическая величина, определяемая работой по перемещению
единичного положительного заряда при удалении его из данной точки
в бесконечность
Напряжённость как градиент потенциала
Слайд 72
Связь между потенциальной силой и потенциальной энергией
Связь между
напряженностью электростатического поля и потенциалом
Слайд 73
Эквипотенциальные поверхности
Геометрическое место точек электростатического поля, в которых
значения потенциала одинаковы
Слайд 74
Эквипотенциальная поверхность это поверхность, в каждой точке которой
потенциал имеет одно и то же значение.
Для всех точек
поверхности выполняется условие
Слайд 76
т.к.
. Единица измерения градиента — В/м.
Слайд 77
Теорема Гаусса для поля в вакууме
Поток вектора напряжённости
электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен
алгебраической сумме заключённых внутри этой поверхности зарядов, делённых на
Слайд 78
Теорема Гаусса для поля в вакууме
Если заряд распределён
в пространстве с объёмной плотностью , то
теорема Гаусса
для электростатического поля в вакууме будет иметь вид
Слайд 79
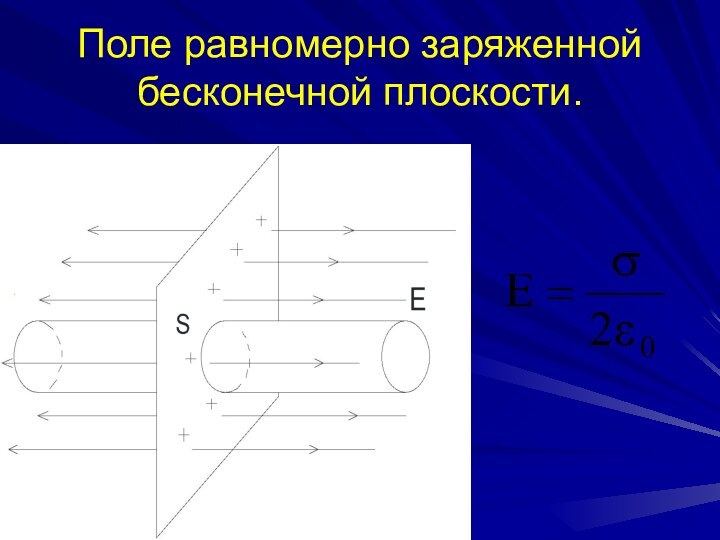
Поле равномерно заряженной бесконечной плоскости.
.
Слайд 80
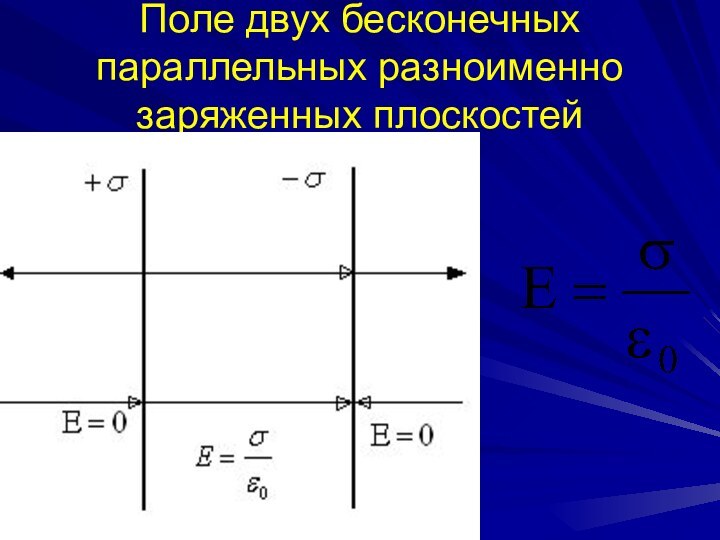
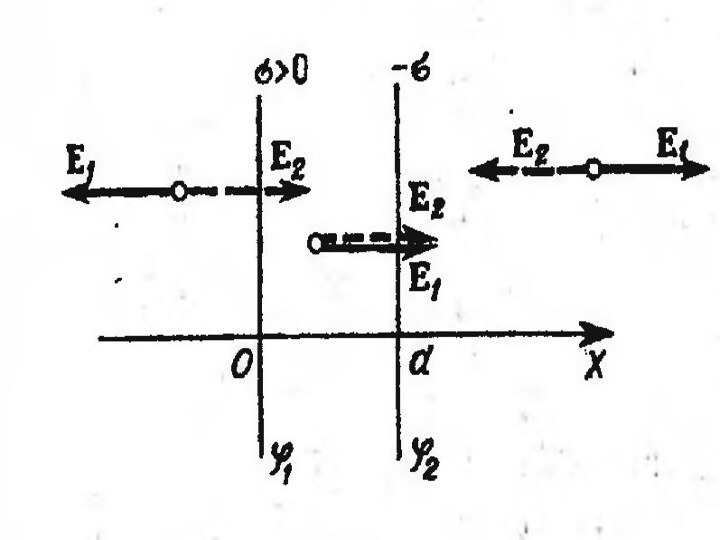
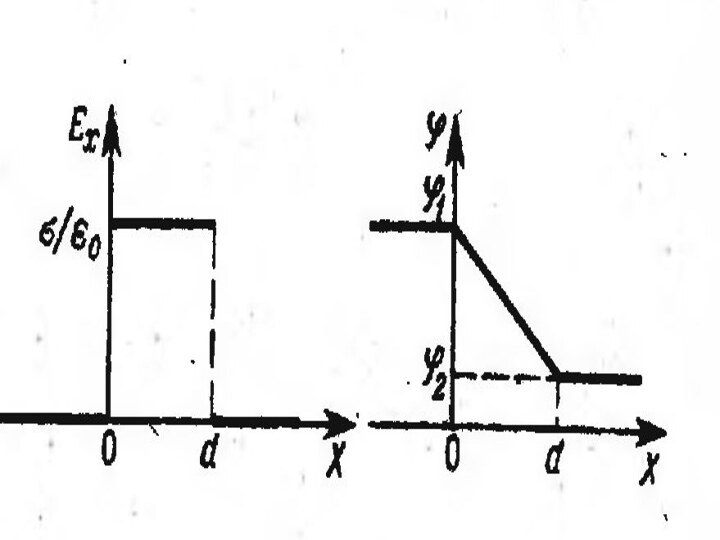
Поле двух бесконечных параллельных разноименно заряженных плоскостей
Слайд 81
Уравнения электростатики в вакууме
Поле двух плоскостей
Слайд 84
Уравнения электростатики в вакууме
Поле равномерно заряженной плоскости
Слайд 86
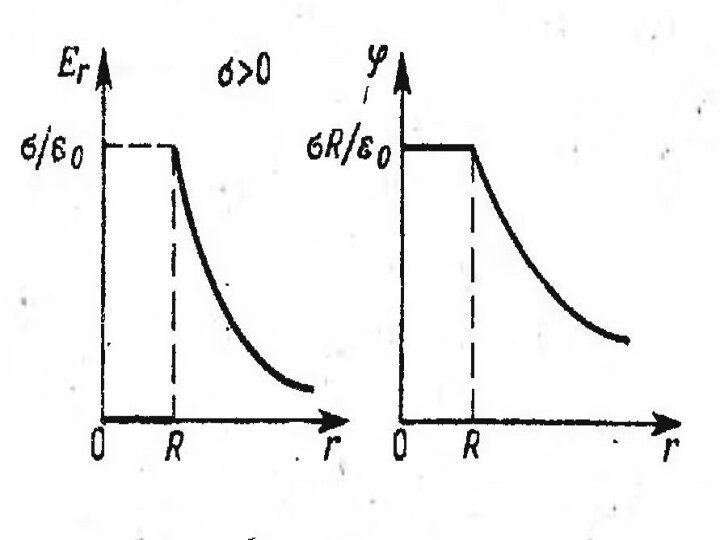
Поле равномерно заряженной сферической
поверхности.
(r ≥ R)
Слайд 88
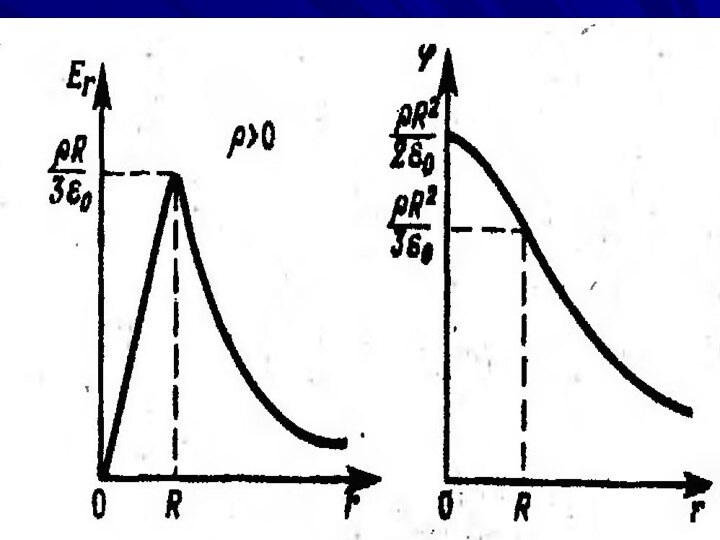
Поле заряда, равномерно распределенного в вакууме по объему
шара
Слайд 90
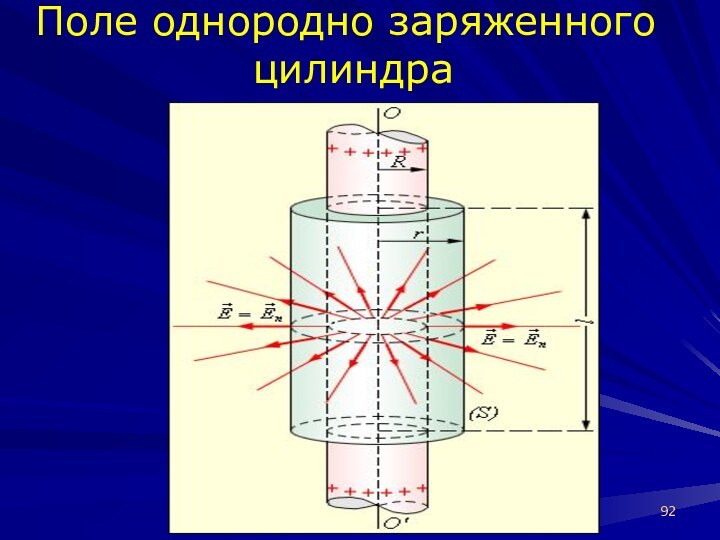
Уравнения электростатики в вакууме
Поле бесконечно длинного заряженного цилиндра
(нити)
Слайд 92
Уравнения электростатики в вакууме
Поле однородно заряженного
цилиндра