- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Электрокапиллярные явления
Содержание
- 2. Электрокапиллярные явления отражают зависимость пограничного натяжения на
- 3. Условия изменения поверхностной энергии в жидких
- 4. Связь пограничного натяжения с обратимой поверхностной работой
- 5. Для жидких электродов dσ/dlns =0, так как
- 6. методы измерения пограничного натяжения жидких электродов.метод стационарных
- 7. Метод стационарных капель Под действием сил пограничного
- 8. метод капиллярного электрометраЖидкий металл находится в вертикальной
- 9. электрокапиллярная кривая Это зависимость пограничного натяжения от
- 10. Качественно такую форму σ,E кривой можно объяснить
- 11. Уравнения Нернста для ртутного электрода
- 12. Уравнение Гиббса для ртутного электрода
- 13. Физический смысл величины ΓHg2 2+Предположим, что на
- 14. основное уравнение электрокапиллярности
- 15. Уравнение Липпмана
- 16. Уравнение электрокапиллярности для бинарного электролита в цепях без переноса
- 17. Уравнение Липпмана для постоянного электрода сравненияпри измерении
- 18. Электрокапиллярный метод позволяет определить заряд электрода, потенциал
- 19. Нахождение Г орг. при постоянной концентрации фонового электролитаварьируют концентрацию органического вещества и используют формулу
- 20. дифференциальная емкость двойного электрического слоя
- 21. Анализ электрокапиллярных кривыхФорма электрокапиллярных кривых зависит от
- 22. Определение природы адсорбцииС ростом концентрации NaF наклон
- 23. Гидратация ионовВ концентрированных (>1 М) раствора поверхностно
- 24. Специфическая адсорбция анионовСпецифическая адсорбция анионов на незаряженной
- 25. Анализ кривыхспецифическая адсорбция галогенид- ионов растет в
- 26. Расчет специфической адсорбции ионовЧтобы рассчитать специфическую адсорбцию
- 28. Анализ капиллярных кривых в присутствии адсорбции полярных
- 29. Полярографический методВ полярографическом методе применяется ртутный капельный
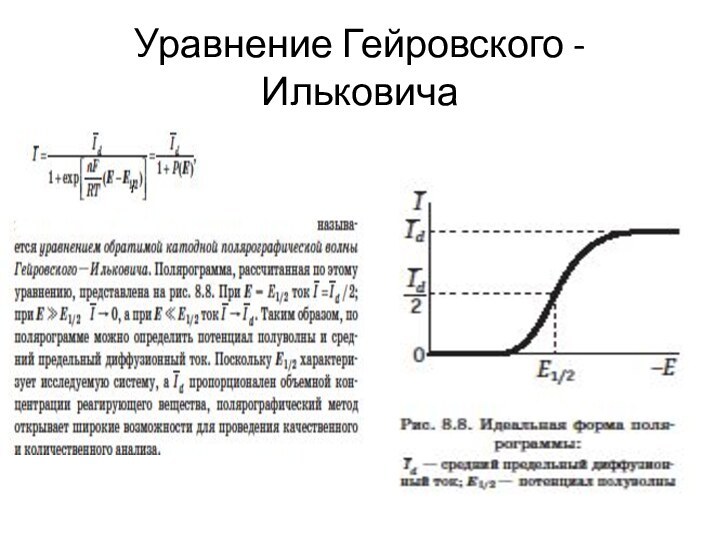
- 30. Уравнение Ильковича
- 31. Скачать презентацию
- 32. Похожие презентации
Электрокапиллярные явления отражают зависимость пограничного натяжения на границе электрод/раствор от потенциала электрода и состава раствора. Для жидких металлов (ртуть, галлий, амальгамы, расплавы) пограничное натяжение γ совпадает обратимой поверхностной работой σ и может быть экспериментально измерено,


























Слайд 2 Электрокапиллярные явления отражают зависимость пограничного натяжения на границе
электрод/раствор от потенциала электрода и состава раствора.
металлов (ртуть, галлий, амальгамы, расплавы) пограничное натяжение γ совпадает обратимой поверхностной работой σ и может быть экспериментально измерено,Слайд 3 Условия изменения поверхностной энергии в жидких металлах
и сплавах
жидкая граница раздела допускает изменение ее поверхности в
обратимых условиях (достаточно, например, наклонить стаканчик со ртутью, покрытой раствором, чтобы изменилась поверхность ртутного электрода). небольшое упругое растяжение твердого электрода приводит к увеличению расстояния между атомами металла на поверхности, а следовательно, растянутая поверхность не идентична первоначальной и имеет иное значение σ
Слайд 5 Для жидких электродов dσ/dlns =0, так как увеличение
поверхности не изменяет ее структуры, а потому γ =
σ.На твердых электродах в области упругой деформации можно измерить γ, тогда как величина σ недоступна для экспериментального определения
величина γ в общем случае является тензором.
Поэтому формулы, связывающие γ со скалярной величиной σ, справедливы только для изотропных поверхностей, работа растяжения которых не зависит от направления приложенной силы.
Слайд 6
методы измерения пограничного
натяжения жидких электродов.
метод стационарных капель основан
на изучении формы металлической капли, расположенной в растворе на
гладкой горизонтальной поверхности.Капиллярного электрометра
Слайд 7
Метод стационарных капель
Под действием сил пограничного натяжения
капля стремится приобрести сферическую форму, так как из всех
тел с равным объемом сфера имеет наименьшую поверхность.С другой стороны, сила тяжести стремится сплющить каплю.
По форме капли с помощью уравнения Лапласа
можно рассчитать σ.
Метод дает абсолютные значения пограничного натяжения, но является весьма трудоемким.
Слайд 8
метод капиллярного
электрометра
Жидкий металл находится в вертикальной трубке, которая
снизу заканчивается коническим капилляром. Капилляр погружен в исследуемый раствор.
Граница
между электродом и раствором находится внутри капилляра, и за ее положением можно следить при помощи горизонтального микроскопа. Изменение потенциала электрода или состава раствора приводит к изменению σ и к перемещению границы раздела внутри капилляра.
если при помощи системы сообщающихся сосудов и подъемника так изменить высоту металла в трубке, чтобы мениск в капилляре занял свое первоначальное положение, то высота столба жидкого металла h оказывается пропорциональной σ.
Константу пропорциональности в соотношении σ = kh определяют по измерениям в растворе заданного состава (например, NaHSO4), для которого σ может быть получена методом стационарных капель.
Слайд 9
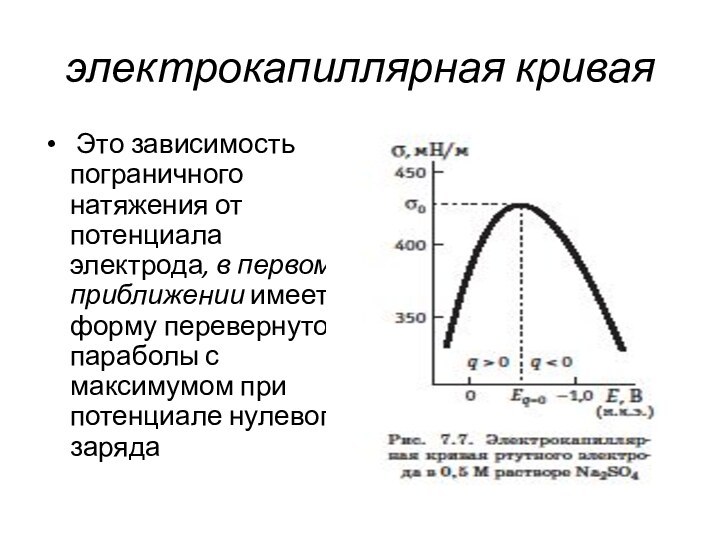
электрокапиллярная кривая
Это зависимость пограничного натяжения от потенциала
электрода, в первом приближении имеет форму перевернутой параболы с
максимумом при потенциале нулевого зарядаСлайд 10 Качественно такую форму σ,E кривой можно объяснить тем,
что отталкивание одноименных зарядов на поверхности металла, которое тем
сильнее, чем больше | q |, уменьшает работу, необходимую для увеличения поверхности электрода, т. е. величину σ
Слайд 13
Физический смысл величины ΓHg2 2+
Предположим, что на единице
поверхности ртути имеется q положительных зарядов.
Чтобы образовать единицу
новой поверхности и создать на ней q положительных зарядов (без подачи зарядов извне), q/2F ионов Hg2 (2+) должно перейти из раствора в металл. При этом концентрация ионов ртути в растворе уменьшится на q/2F и такое же количество ионов ртути надо внести в раствор для сохранения его первоначального состава. Следовательно,
Слайд 17
Уравнение Липпмана для постоянного электрода сравнения
при измерении электрокапиллярных
кривых потенциал ртутного электрода измеряют относительно постоянного электрода сравнения,
который отделен от исследуемого электролитическим мостиком, заполненным насыщенным раствором KCl или NH4NO3 для элиминирования диффузионного потенциала используется уравнение Липпмана
Слайд 18
Электрокапиллярный метод позволяет определить
заряд электрода,
потенциал нулевого
заряда,
поверхностные избытки катионов и анионов,
а также нейтральных
органических молекул — Горг.
Слайд 19
Нахождение Г орг. при постоянной концентрации фонового электролита
варьируют
концентрацию органического вещества и используют формулу
Слайд 21
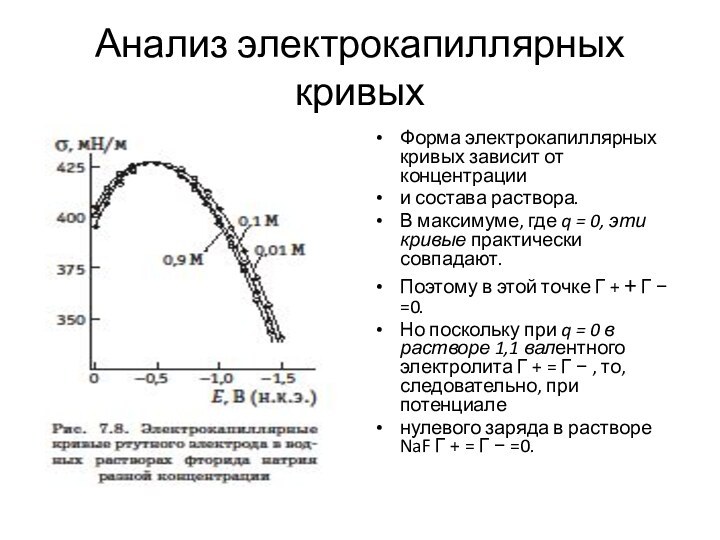
Анализ электрокапиллярных кривых
Форма электрокапиллярных кривых зависит от концентрации
и
состава раствора.
В максимуме, где q = 0, эти
кривые практически совпадают. Поэтому в этой точке Γ + + Γ − =0.
Но поскольку при q = 0 в растворе 1,1 валентного электролита Γ + = Γ − , то, следовательно, при потенциале
нулевого заряда в растворе NaF Γ + = Γ − =0.
Слайд 22
Определение природы адсорбции
С ростом концентрации NaF наклон восходящего
и нисходящего участков σ,Е кривой становится более крутым
Если предположить,
что адсорбция ионов Na+ и F– обусловлена только электростатическими силами, то, исходя из уравнения Липпмана, можно ожидать сдвига ветвей σ,Е кривой, равного при значительном удалении от Еq=0 приблизительно 59 мВ для изменения концентрации NaF в 10 раз.Согласие экспериментальных данных с таким выводом можно рассматривать как подтверждение электростатической природы адсорбции ионов Na+ и F–.
Слайд 23
Гидратация ионов
В концентрированных (>1 М) раствора поверхностно -
неактивных электролитов вблизи потенциала нулевого заряда наблюдается увеличение σ
с ростом концентрации.это указывает на отрицательную адсорбцию соли: Г+ = Г– < 0.
Ее причиной является гидратация ионов, в результате которой между поверхностью электрода и ионами оказывается слой молекул растворителя.
Слайд 24
Специфическая адсорбция анионов
Специфическая адсорбция анионов на незаряженной поверхности
ртутного электрода проявляется в снижении электрокапиллярного максимума, а возникновение
скачка потенциала между слоем специфически адсорбированных анионов и притянутыми к ним катионами — в сдвиге потенциала нулевого заряда в отрицательную сторону по сравнению с Eq=0 в растворе NaF.
Слайд 25
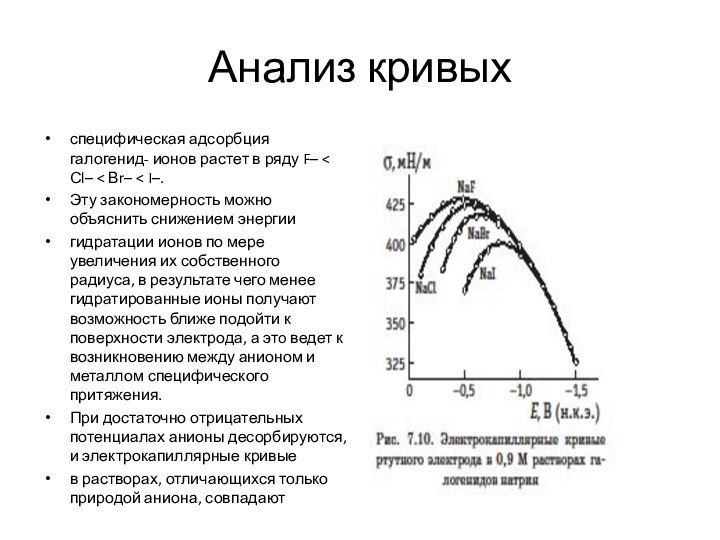
Анализ кривых
специфическая адсорбция галогенид- ионов растет в ряду
F– < Сl– < Вr– < I–.
Эту закономерность можно
объяснить снижением энергиигидратации ионов по мере увеличения их собственного радиуса, в результате чего менее гидратированные ионы получают возможность ближе подойти к поверхности электрода, а этo ведет к возникновению между анионом и металлом специфического притяжения.
При достаточно отрицательных потенциалах анионы десорбируются, и электрокапиллярные кривые
в растворах, отличающихся только природой аниона, совпадают
Слайд 26
Расчет специфической адсорбции ионов
Чтобы рассчитать специфическую адсорбцию ионов,
которая практически равна их поверхностной концентрации Ai, электрокапиллярные измерения
проводят в смесях поверхностно- активного и поверхностно-неактивного электролитов с постоянной ионной силой , например:mcMNaI + (1 – m)c M NaF, (7.3.А)
где с — общая концентрация смеси; т — доля поверхнoстно- активного электролита.
Слайд 28 Анализ капиллярных кривых в присутствии адсорбции полярных органических
веществ
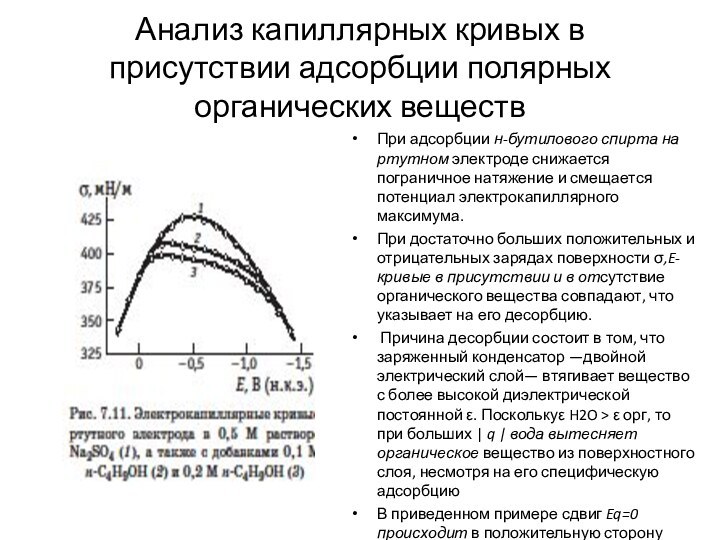
При адсорбции н-бутилового спирта на ртутном электроде снижается пограничное
натяжение и смещается потенциал электрокапиллярного максимума. При достаточно больших положительных и отрицательных зарядах поверхности σ,E-кривые в присутствии и в отсутствие органического вещества совпадают, что указывает на его десорбцию.
Причина десорбции состоит в том, что заряженный конденсатор —двойной электрический слой— втягивает вещество с более высокой диэлектрической постоянной ε. Посколькуε H2O > ε орг, то при больших | q | вода вытесняет органическое вещество из поверхностного слоя, несмотря на его специфическую адсорбцию
В приведенном примере сдвиг Eq=0 происходит в положительную сторону
Слайд 29
Полярографический метод
В полярографическом методе применяется ртутный капельный электрод
(рис. 8.6).
Он состоит из длинного узкого капилляра, на
конце которого периодически образуются и отрываются небольшие ртутные капли (диаметром около 1–2 мм). Поляризация капли осуществляется относительно большого ртутногоэлектрода на дне ячейки,
потенциал измеряется по отношению к
постоянному электроду сравнения (обычно это нормальный или
Насыщенный каломельныйэлек трод).
Ток в цепи капельного электрода оказывается функцией времени.
Зависимость среднего тока I от потенциала Е называется полярограммой.