Презентация на тему Индукция

была причина изменения магнитного потока, охватываемого замкнутым проводящим контуром,

Знак минус отражает правило Ленца

индукции при движения контура в постоянном магнитном поле объясняется

неподвижных проводниках Максвелл предположил, что всякое переменное магнитное поле

Циркуляция вектора E этого поля по любому неподвижному контуру L проводника представляет собой э. д. с. электромагнитной индукции:

C другой стороны по закону Фарадея:

Приравняв эти выражения получим:

Циркуляция электрического поля, создаваемого изменяющимся магнитным полем отлична от нуля, значит, это поле не является потенциальным, а является как и магнитное поле вихревым.

создает вокруг себя магнитное поле, индукция которого, пропорциональна току:

Магнитный поток

Следовательно

Запишем в виде равенства

Коэффициент пропорциональности L называется индуктивностью контура. Индуктивность зависит от геометрических размеров и формы контура, а также от магнитных свойств окружающей среды.

Единицей индуктивности является генри (Гн). Индуктивностью 1Гн обладает контур, магнитный поток сквозь который при силе тока 1А равен 1Вб

функцию тока: B=B(I).
2). Вычислить полный магнитный поток:
3).

l, имеющий N витков, по которому течет ток I

Индукцию магнитного поля внутри соленоида рассчитаем, применяя теорему о циркуляции.

Выберем замкнутый прямоугольный контур ABCDA, как показано на рис.

Циркуляция вектора B по замкнутому контуру ABCDA, охватывающему все N витков, равна

четырех интегралов:

На участках ВС и DA контур

Остается только один интеграл:

Выражение для магнитной индукции поля внутри соленоида примет вид:

n=N/l - число витков на единицу длины

Магнитное поле внутри соленоида однородно.

S равен

Полный магнитный поток, пронизывающий N витков, равен

3).

V=Sl объем соленоида.

Для соленоида с сердечником:

μ - магнитная проницаемость среды

при изменении в нем силы тока называется самоиндукцией.
Для получения

Если при изменении тока индуктивность L остается постоянной, то

Знак минус показывает, что εs всегда направлена так, чтобы препятствовать изменению силы тока

расположенных достаточно близко друг от друга.
Если в контуре

Часть магнитного потока, которая пронизывает контур 2

где L21 — коэффициент пропорциональности.

Если ток I1 изменяется, то в контуре 2 индуцируется э.д.с. εi2, которая по закону Фарадея равна

поток (его поле изображено штриховыми линиями) пронизывает первый контур.

Часть магнитного потока, которая пронизывает контур 1

Если ток I2 изменяется, то в контуре 1 индуцируется э.д.с. εi1, которая по закону Фарадея равна

Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией.

контуров.
Коэффициенты L12 и L21 зависят от геометрической формы,

При отсутствии ферромагнетиков

(Теорема взаимности).

Единица взаимной индуктивности — генри (Гн)

которому течет ток I.
Магнитный поток, создаваемый полем этого

При изменении тока на dI магнитный поток изменяется на dΦ

Для изменения магнитного потока необходимо совершить работу

Тогда работа по созданию магнитного потока Ф будет равна

энергию магнитного поля непосредственно через индукцию магнитного поля B

Так как

Индукция магнитного поля соленоида равна

Выразим

Подставим в выражение для энергии магнитного поля

плотности энергии магнитного поля получено для однородного поля, но

поля, ε - диэлектрическая проницаемость среды
- электрическая постоянная

Для сравнения:

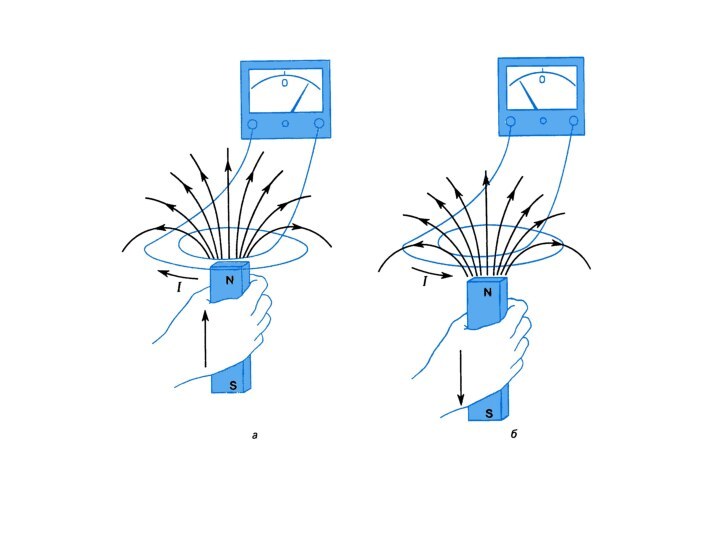
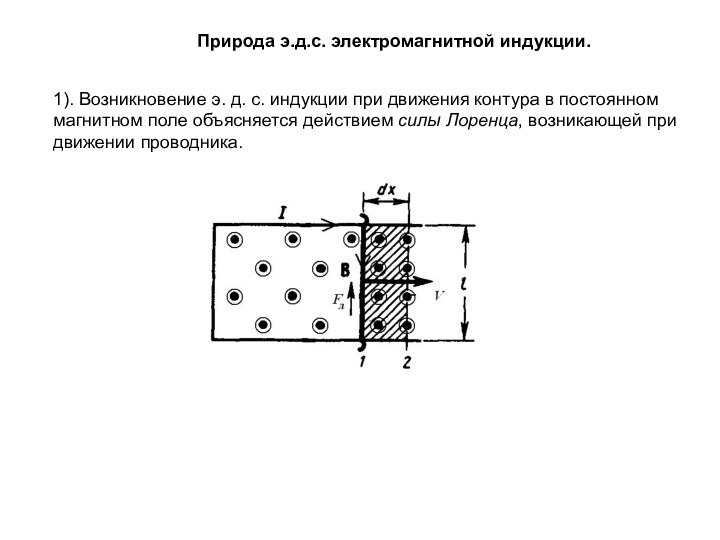
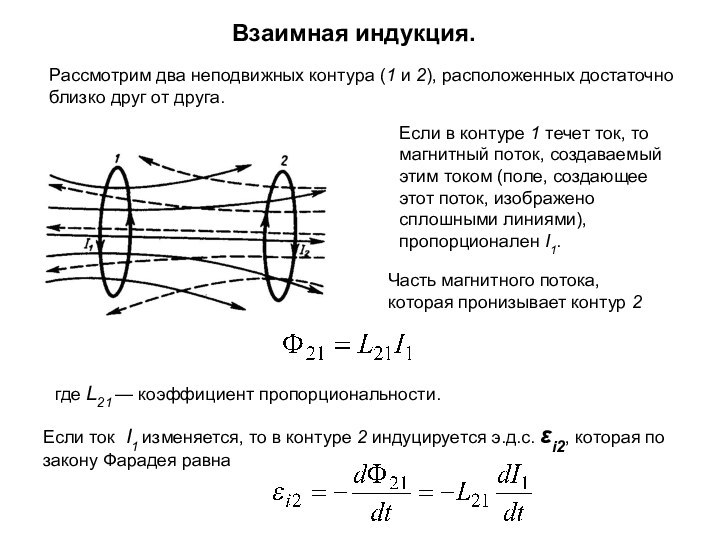
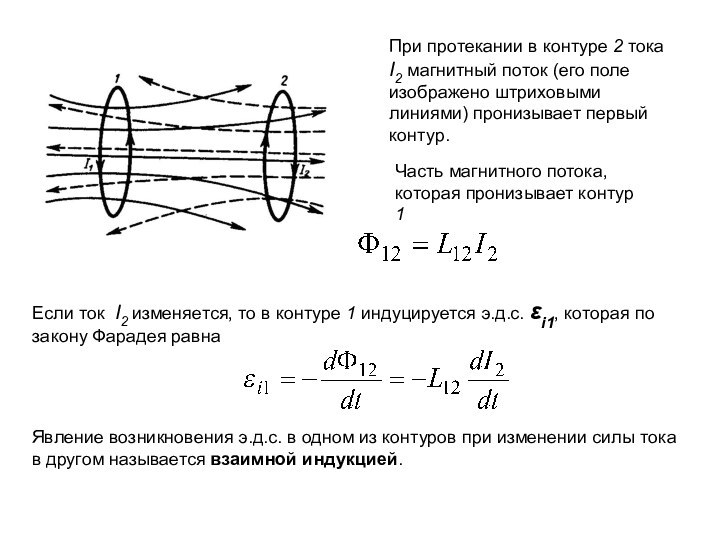
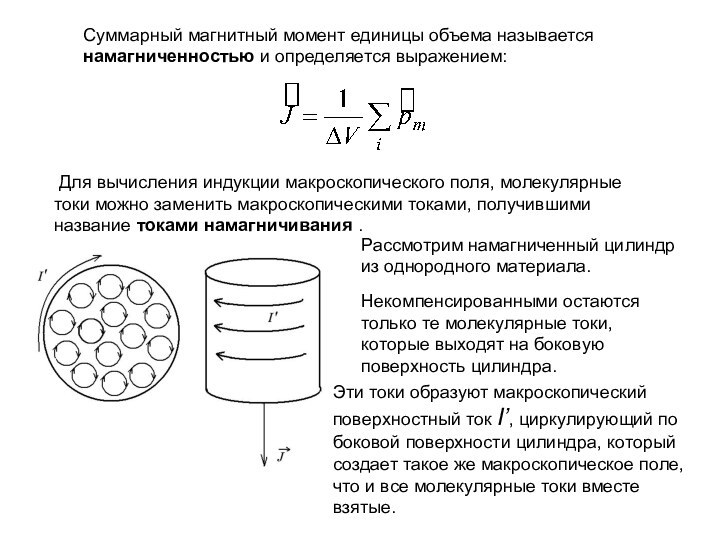
магнитное поле внести вещество, то поле изменяется, так как

Это можно объяснить тем, что каждый движущийся вокруг ядра атома электрон представляет собой элементарный круговой ток.

В отсутствие внешнего поля орбиты молекулярных токов, а, следовательно, и их магнитные моменты

ориентированы хаотически в пространстве так, что вещество не проявляет никаких магнитных свойств.

При наложении внешнего магнитного поля моменты ориентируются вдоль силовых линий этого поля - вещество намагничивается.

определяется выражением:

Для вычисления индукции макроскопического поля, молекулярные

Рассмотрим намагниченный цилиндр из однородного материала.

Некомпенсированными остаются только те молекулярные токи, которые выходят на боковую поверхность цилиндра.

Эти токи образуют макроскопический поверхностный ток I’, циркулирующий по боковой поверхности цилиндра, который создает такое же макроскопическое поле, что и все молекулярные токи вместе взятые.

замкнутому контуру равна алгебраической сумме токов намагничивания, охватываемых этим

Напряженность магнитного поля H.

Циркуляция вектора B, определяется не только токами проводимости, но и токами намагничивания

Выражая ток намагничивания через циркуляцию вектора намагниченности, получим

Величину, стоящую в скобках, называют напряженностью магнитного поля:

замкнутому контуру равна алгебраической сумме токов проводимости, охватываемых этим

Размерность напряженности магнитного поля

Вектор намагниченности и напряженность магнитного поля связаны следующим соотношением:

где χ - магнитная восприимчивость, зависящая от свойств магнетика.

χ<0 для диамагнетиков

χ>0 для парамагнетиков