Презентация на тему Инерция

точек
с массами

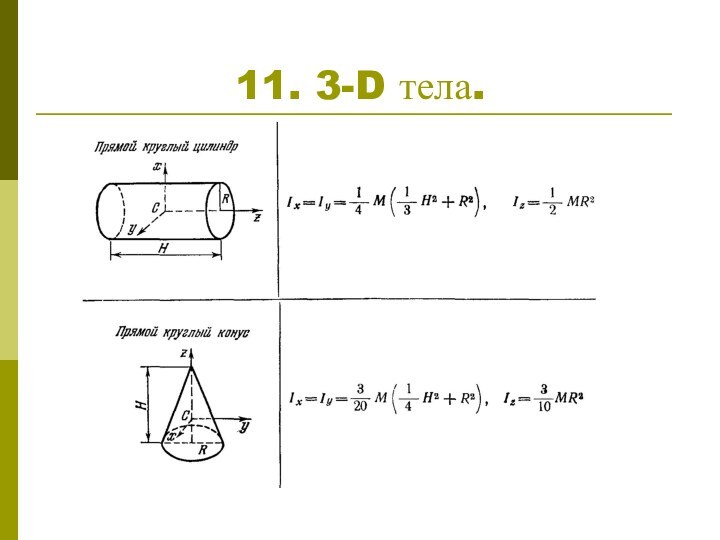
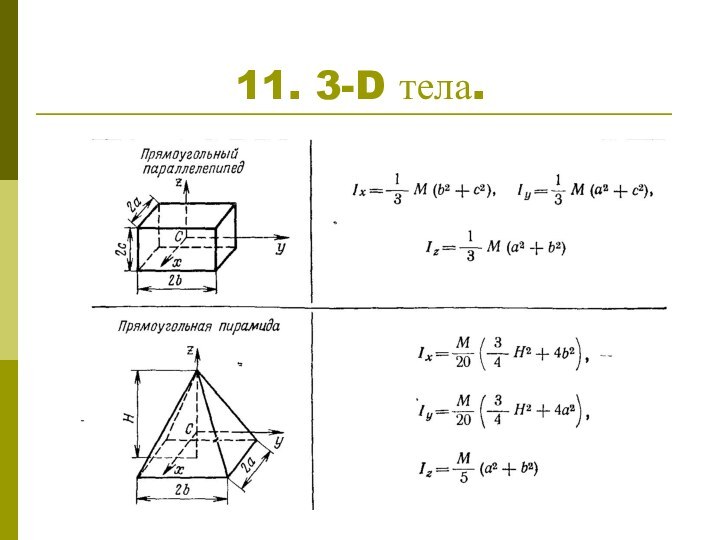
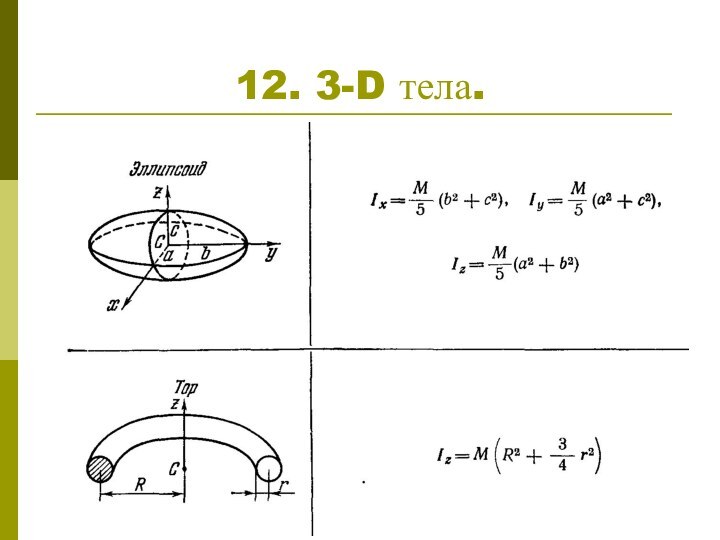
1. Определение момента инерции

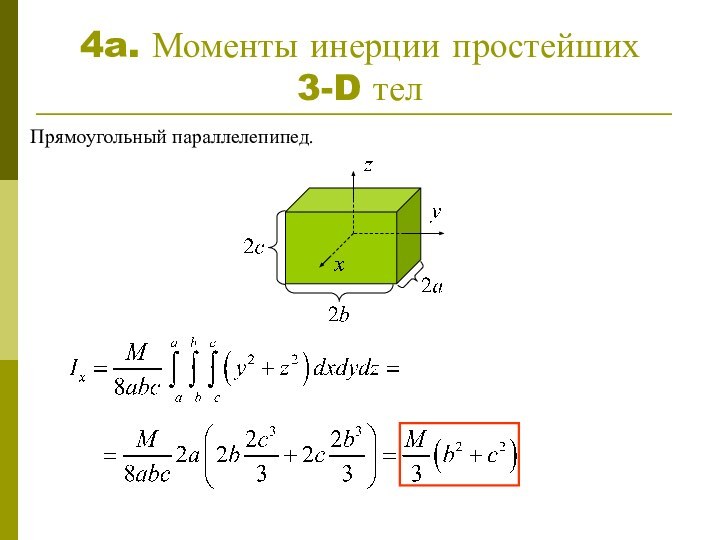
Для непрерывно распределенных масс

Для однородного ( ) тела

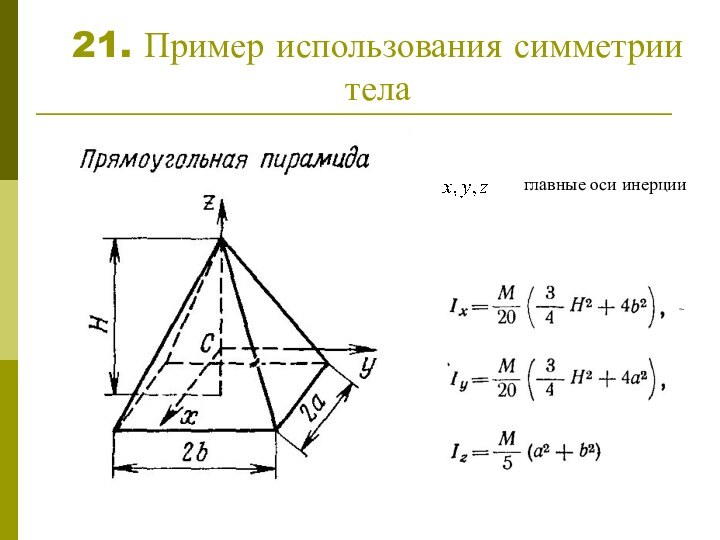
Задача:
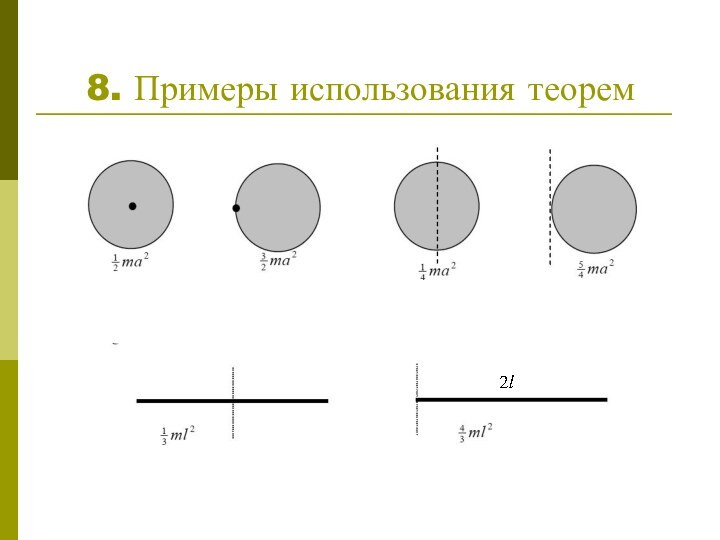
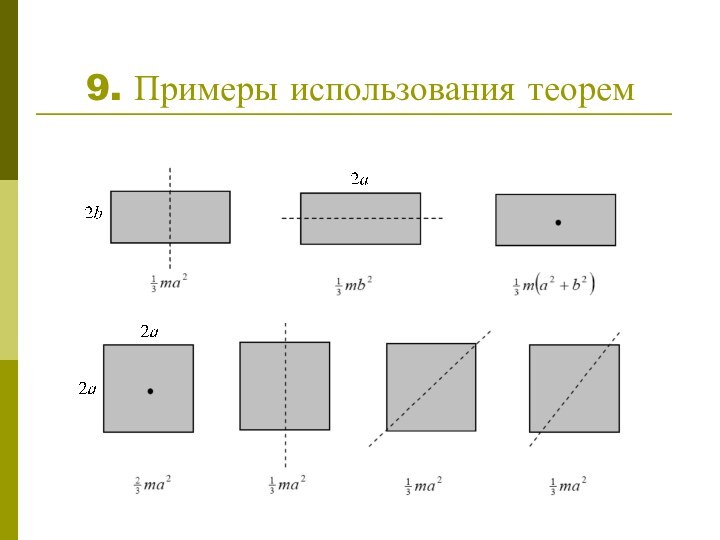
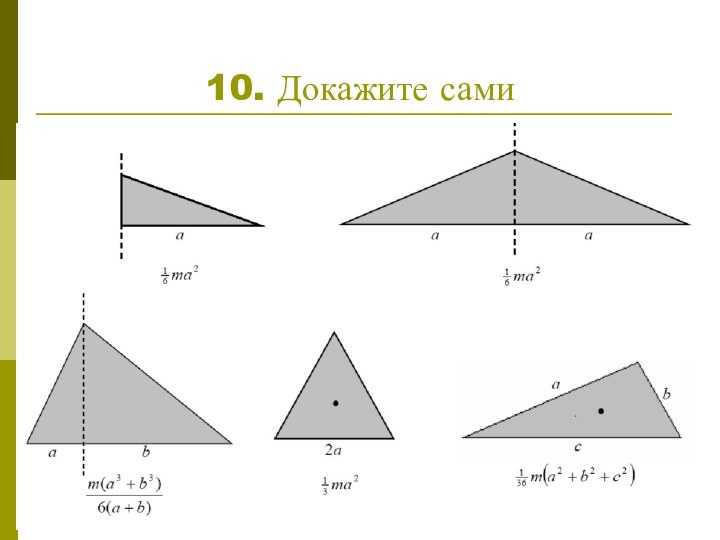
научиться считать момент инерции любого тела относительно любой оси

меру инерции тела во вращательном движении
Произведение момента инерции

сравните

вращательное движение

поступательное движение

Ось проходит через середину стержня, перпендикулярно ему

Ось проходит через середину диска, перпендикулярно ему

треугольник. Ось проходит через катет

через центр
Из соображений симметрии

в виде
Стержень
Диск
Треугольник
Параллелепипед
Шар
Величина называется радиусом инерции

По определению радиус инерции есть длина, равная расстоянию от данной оси той точки, в которой нужно сосредоточить массу всей системы, чтобы получить тот же момент инерции.

инерции IC тела относительно параллельной оси, проходящей через масс

6. Теорема (Гюйгенса-Штейнера) о параллельных осях

Очевидное обобщение

плоскости фигуры, равен сумме моментов инерции фигуры относительно двух

7. Теорема о перпендикулярных осях

точки
моменты инерции относительно осей
центробежные
моменты инерции

Положительная определенность
3) Неравенства для
Геометрическое толкование: из трех отрезков,

4) Неравенства для

поверхность уровня
В силу положительной определенности поверхностью уровня

Физический смысл эллипсоида инерции

Проведем через начало координат в направлении оси прямую до пересечения с эллипсоидом инерции. Обозначим через длину соответствующего отрезка, а через координаты точки пересечения.

Длина радиуса-вектора эллипсоида инерции обратно пропорциональна корню квадратному из момента инерции относительно оси, направленной по этому радиусу

если перейти к новым координатным осям

Уравнение эллипсоида инерции в новых осях

Тензор инерции в новых осях

Как найти главные оси?

1) Найти решения характеристического уравнения

- единичная матрица

2) Найти собственные вектора как нетривиальное решение уравнения

При этом собственные числа совпадают с , а собственные вектора определят направление главных осей

трехосный эллипсоид

эллипсоид вращения

шаровой эллипсоид

с

17. Главные оси инерции

В более широком смысле для данной точки главной осью инерции тела называется ось, для которой оба центробежных момента инерции, содержащие индекс этой оси, равны нулю.

Свойство быть главной осью не зависит от выбора направлений двух других координатных осей.

Возможный вид тензора инерции

из главных осей тензора инерции. Выберем две другие оси

18. Главные оси инерции и главные оси тензора инерции

Ось является главной осью инерции тогда и только тогда когда она совпадает с одной из главных осей тензора инерции.

Пусть ось является главной осью инерции

называется главная ось, проходящая через центр масс тела
Свойство быть

Для того, чтобы ось была главной для точки необходимо и достаточно, чтобы центр масс тела находился на этой оси

Пусть ось главная для точки

Главная центральная ось инерции является главной осью для всех своих точек, а нецентральная главная ось инерции является главной осью инерции лишь для одной своей точки

симметрии
Если однородное абсолютно твердое тело имеет ось

Тогда каждой частице будет соответствовать такая же частица

Eсли однородное абсолютно твердое тело имеет плоскость симметрии, то для всех точек этой плоскости одна из главных осей инерции будет к ней
перпендикулярна

тела известны главные центральные моменты инерции
Дана прямая

1) Проводим прямую через центр масс

2) Находим углы между и главными осями инерции

3) Вычисляем момент инерции относительно оси

4) По теореме Гюйгенса-Штейнера вычисляем момент инерции относительно оси

относительно образующей SB; радиус основания конуса равен R, высота

главные центральные оси инерции

по таблицам