Слайд 2
Кінетичні явища
(явища переносу)
Причина явищ – електрони провідності в
своєму русі переносять звязані з ними фізичні величини: масу,
електричний заряд, енергію та ін. В результаті чого при певних умовах виникають направлені потоки цих величин, що приводить до ряду електричних і теплових ефектів.
1. Електропровідність.
2. Ефект Холла.
3. Зміна опору в магнітному полі.
4. Термоерс.
5. Ефект Томсона.
6. Ефект Пельтє.
7. Ефект Нернста-Етінгсгаузена.
8. Ефект Рігі-Ледюка.
9. Повздовжні термомагнітні ефекти.
10. Дифузія.
11. Теплопровідність
Слайд 3
1. Електропровідність.
В результаті невпорядкованого теплового руху в електронному
газі в стані теплової рівноваги не має переважних напрямів
руху, і тому середнє значення теплової швидкості рівне нулю.
При накладанні зовнішнього електричного поля електрони отримують додаткову швидкість під дією поля. В цьому випадку результуючий рух електронів вже не є зовсім невпорядкованим і виникає направлений потік електричного заряду (електричний струм).
Слайд 4
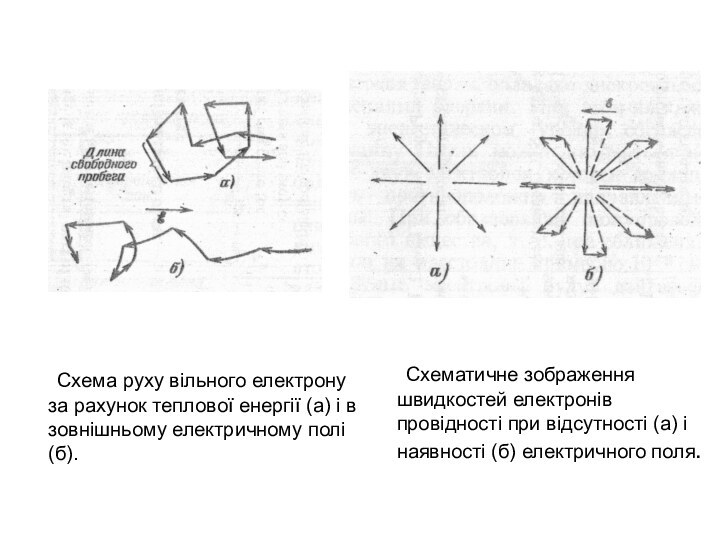
Схема руху вільного електрону за рахунок теплової енергії
(а) і в зовнішньому електричному полі (б).
Схематичне зображення швидкостей
електронів провідності при відсутності (а) і наявності (б) електричного поля.
Слайд 5
Відстань, яку проходить вільний носій заряду між двома
зіткненнями, називається довжиною вільного пробігу, а усереднене значення всіх
відрізків шляху є середня довжина вільного пробігу.
Час між двома зіткненнями і його усередене значення називається часом вільного пробігу і середнім часом вільного пробігу.
Середня довжина вільного пробігу l і середній час вільного пробігу τ звязані співвідношенням
l=v0 × τ
де v0 - середня швидкість теплового руху вільного носія.
В напвпровідниках при кімнатній температурі
v0 ≈ 107 см/с.
Слайд 6
Фактично рух електрону в кристалі складається з невпорядкованого
теплового і впорядкованого руху, визваного дією зовнішнього електричного поля.
Направлений
рух сукупності носіїв заряду в електричному полі називається дрейфом, а швидкість їх направленого руху називається дрейфовою швидкістю.
Слайд 7
В багатьох випадках дрейфова швидкість vd пропорційна напруженості
електричного поля Ε.
Vd = μ Ε
Дрейфова рухливість заряджених
частинок μ є швидкість, яку отримує частинка в полі з напруженістю одиниця.
Для негативних частинок μ відємна,
для позитивних частинок μ додатня.
Густина струму j
j=envd = enμ Ε
де e - заряд однієї частинки, n - концентрація рухливих частинок.
Закон Ома в диференційній формі
j= σ Ε
де σ - питома електропровідність речовини.
σ = enμ
Слайд 8
Електропровідність напівпровідників
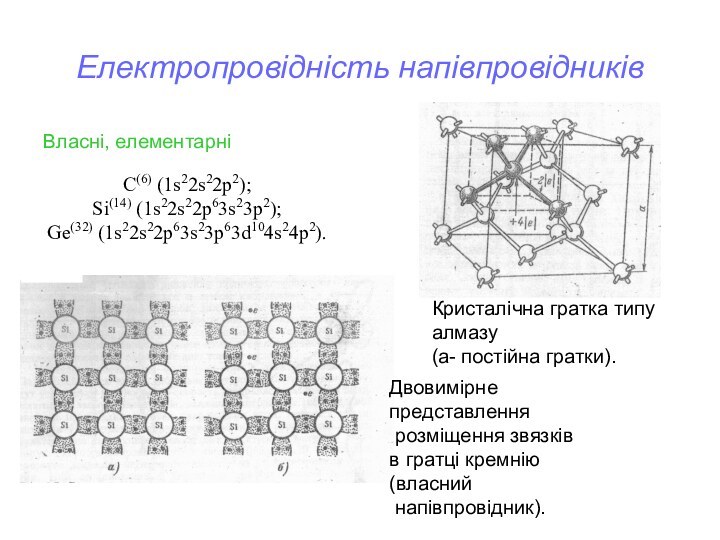
Власні, елементарні
C(6) (1s22s22p2);
Si(14) (1s22s22p63s23p2);
Ge(32) (1s22s22p63s23p63d104s24p2).
Кристалічна гратка типу
алмазу
(а- постійна гратки).
Двовимірне представлення
розміщення звязків
в гратці
кремнію (власний
напівпровідник).
Слайд 9
Процес перетворення звязаного електрона у вільний електрон називається
генерацією.
Процес перетворення вільного електрона у звязаний називається рекомбінацією.
Фактичний рух
електрона в кристалі складається з невпорядкованого теплового і впорядкованого руху, який визивається дією зовнішнього електричного поля.
Механізм провідності обумовлений рухом звязаних електронів по вакантним звязкам отримав назву діркової провідності.
Слайд 10
В чистому напівпровіднику, що не містить домішок, відбувається
електронна і діркова електропровідність. Відповідно електричний струм у власному
напівпровіднику визначається двома складовими – електронним і дірковим струмом, що протікають в одному напрямі.
Схематичне зображення енергетичних зон
власного напівпровідника.
Слайд 11
Електропровідність напівпровідників
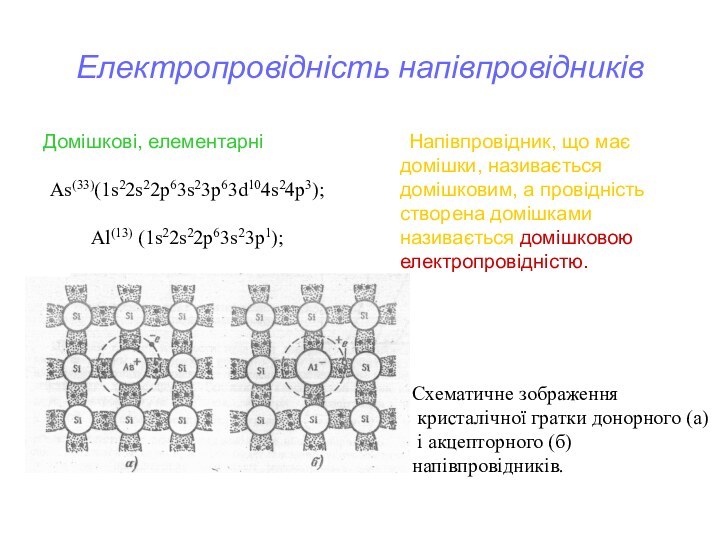
Домішкові, елементарні
As(33)(1s22s22p63s23p63d104s24p3);
Al(13) (1s22s22p63s23p1);
Схематичне зображення
кристалічної гратки донорного
(а)
і акцепторного (б) напівпровідників.
Напівпровідник, що має домішки, називається
домішковим, а провідність створена домішками називається домішковою електропровідністю.
Слайд 12
Домішка, що віддає електрон називається донорною.
Якщо домінуючу роль
в провідності напівпровідника відіграють електрони, то вони є основними
носіямизаряду, а дірки – неосновними носіями заряду. Такий напівпровідник називається електронним або n – типу.
Домішка, що захоплює електрон називається акцепторною.
Якщо кількість дірок значно більша кількості вільних електронів, то електропровідність кристалу буде дірковою. В такому напівпровіднику основними носіями заряду будуть дірки, а електрони – неосновні носії заряду. Напівпровідник з акцепторною домішкою називається дірковим або p – типу.
Енергетична діаграма
донорного (а) і
акцепторного (б)
напівпровідників
Слайд 13
В ізотропних речовинах дрейфова швидкість направлена або паралельно
полю (у позитивних частинок), або протилежно полю (у відємних
частинок), тому μ і σ скаляри і , відповідно вектори j і Ε співпадають по напрямку.
В анізотропних речовинах це не має місця і співвідношення між j і Ε має більш загальний вид
jx = σ xx Ε x + σ xy Ε y + σ xz Ε z ,,
jy = σ yx Ε x + σ yy Ε y + σ yz Ε z ,,
jz = σ zx Ε x + σ zy Ε y + σ zz Ε z ,,
Або в скороченому записі
jα = σα β Ε β (α , β = x, y, z).
В цьому випадку явище переносу заряда визначається вже не єдиним кінетичним коефіцієнтом, сукупністю коефіцієнтів σα β , які є компонентами тензора 2-го рангу – тензора електропровідності.
Слайд 14
2. Ефект Холла.
(Гальваномагнітні явища)
Ефект Холла полягає в тому,
що в провіднику зі струмом, який поміщений в магнітне
поле, зявляються електрорушійні сили і, як наслідок, виникає додаткове електричне поле.
Слайд 15
Ε Y = U / d = RBj
= RB I / ad
R – постійна Холла; d
- товщина зразка; a – ширина зразка; I - повний струм
Знак кута Холла: а) ϕ >0; б) ϕ <0.
Сила Лоренца
Fm = q/c v×B.
Слайд 16
Вираз кута Холла через компоненти тензора електропровідності в
магнітному полі σα β
tgϕ= Ε y /Ε x
= - σyx /σyy = σxy /σxx
(σxy =- σyx ; σxx =- σyy )
Вираз постійної Холла через компоненти тензора електропровідності в магнітному полі σα β
R = 1/B× σxy /(σ2xx+ σ2xy)
(Ε y = σxy /(σ2xx+ σ2xy) ×jx)
Технічні застосування ефекта Холла:
- вимірювання напруженості магнітного поля;
- вимірювання сили струму і потужності (В- відоме);
- генерація, модуляція і демодуляція електричних коливань;
- квадратичне детектування коливань;
- підсилення електричних сигналів;
- та ін.
Слайд 17
3. Зміна опору в магнітному полі.
Зовнішнє магнітне поле
викликає зміну jx
-Δσ⊥/σ = Δρ⊥/ρ =χ⊥B2
χ⊥- коефіцієнт поперечного магнітоопору
(залежить від властивостей матеріалу).
σ⊥(B)= jx / Ε x = (σ2xx+ σ2xy) / σ2xx
Якщо магнітне поле паралельне струму, поздовжній магнітоопір ΔρII/ρ =0
Слайд 18
4. Термоерс.
(термоелектричні явища)
Між кінцями розімкненого провідника, які мають
різну температуру, виникає різниця потенціалів, а значить всередині провідника
зявляється електрорушійна сила.
Причина ефекту – потік дифузії заряджених частинок від нагрітого кінця до холодного більший, ніж в зворотньому напрямку.
На кінцях провідника (і на його поверхні) зявляються електричні заряди, а в середині – електричне поле.
dV0 = αdT
α- диференційна термоерс.
Слайд 19
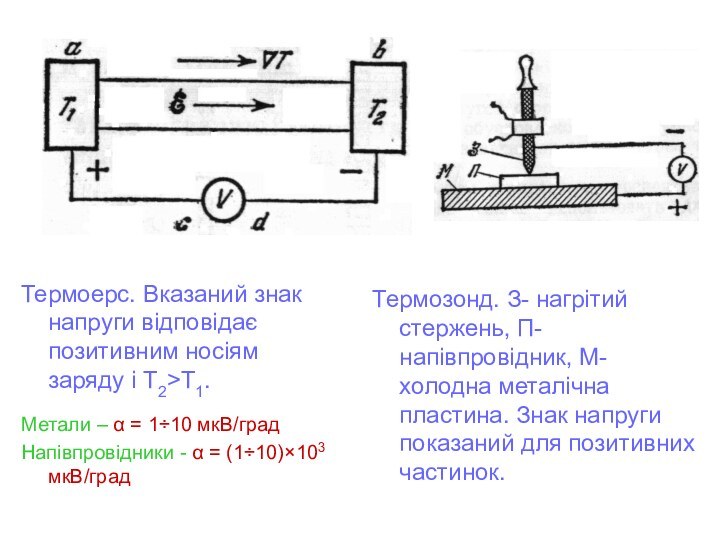
Термоерс. Вказаний знак напруги відповідає позитивним носіям заряду
і Т2>Т1.
Метали – α = 1÷10 мкВ/град
Напівпровідники - α
= (1÷10)×103 мкВ/град
Термозонд. З- нагрітий стержень, П- напівпровідник, М- холодна металічна пластина. Знак напруги показаний для позитивних частинок.
Слайд 20
5. Ефект Томсона.
Якщо в однорідному провіднику є градієнт
температури в напрямку осі Х і в тому ж
напрямку тіче електричний струм густиною j , то в кожній одиниці обєму за одиницю часу виділяється, крім тепла Джоуля j2/σ ще додаткове тепло
-αT j dT/dx.
αT- коефіцієнт Томсона.
При зміні напрямку струму на зворотній тепло Томсона міняє знак: замість поглинання тепла спостерігається його виділення, і навпаки.
При наявності градієнта температури в провіднику є ще тепловий потік, обумовлений теплопровідністю речовини.
Слайд 21
Кількість тепла, що проходить через одиницю поверхні за
одиницю часу в напрямку Х є
-χ dT/dx,
де
χ – коефіцієнт теплопровідності.
Якщо цей потік змінюється в просторі (в результаті зміни χ чи dT/dx ), то в обємі провідника також виділяється тепло.
d/dx(χ dT/dx).
В загальному випадку, коли напрям j і ∇T не співпадає, повна генерація тепла в одиниці обєму за одиницю часу рівна
QV = j2 / σ - αT(j ∇T) + div (χ ∇T).
В стаціонарному випадку QV = 0.
Тому в провіднику встановлюється такий просторовий розподіл температури, при якому тепло, що відводиться теплопровідністю, як раз дорівнює сумі тепла Джоуля і тепла Томсона.
Слайд 22
6. Ефект Пельтє.
Зворотнє виділення тепла спостерігається на границі

контакту двох різних провідників. Кількість тепла, що виділяється на
одиниці площі контакту за одиницю часу Q, рівне
Qs = П12 j.
де j - густина струму через контакт, а П12 - коефіцієнт Пельтє. Він залежить від властивостей провідників, що контактують.
При зміні напрямку струму на зворотній замість виділення тепла спостерігається його поглинання і навпаки. Тобто, П12 = -П21.
Причина виділення (поглинання) тепла Пельтє полягає в тому, що середні енергії електронів Е1 і Е2 в різних провідниках 1 і 2 неоднакові, навіть якщо обидва провідники мають одну і ту ж температуру. При переході з одного провідника в другий змінюється:
1)Потенціальна енергія електрона -eϕ, оскільки на границі розділу є скачок електростатичного потенціалу і тому ϕ1 ≠ ϕ2 .
2) Може змінюватись середня кінетична енергія Е . Причина- не класична статичтика Максвела-Больцмана для електронів, а квантова статистика Фермі-Дірака, у відповідності до якої залежить не лише від температури, але і від концентрації електронів.
Слайд 23
При наявності струму для підтримки температури контакту постійною
від нього необхідно відводити енергію, якщо Е1 > Е2
(виділення тепла Пельтє), або підводити її до контакту, коли Е1<Е2 (поглинання тепла Пельтє).
П12 = П1 – П2.
де П1 і П2 – коефіцієнти Пельтє для провідника 1 і провідника 2, відповідно.
Зв’язок термоелектричних кінетичних коефіцієнтів:
П = α Т,
αT =Т α/dT
Технічне застосування:
-термоелектричні генератори невеликої потужності;
- термоелектричні охолоджуючі пристрої.
Слайд 24
7. Ефект Нернста-Етінгсгаузена.
(термомагнітні ефекти)
Поперечний ефект Нернста-Етінгсгаузена.
Якщо провідник, в
якому є градієнт температури, помістити в магнітне поле, то
в ньому виникне електричне поле Ε перпендикулярне до ∇T и B, тобто в напрямку вектора [∇T× B]. Якщо градієнт температури направлений вздовж осі Х, а магнітна індукція – вздовж осі Z, то електричне поле паралельне осі Y.
Εy = q⊥ Bz dTdx.
q⊥- постійна Нернста-Етінгсгаузена.
Ge: ρ ~1 Ом см , B ~ 103 Гс, dT/dx ~ 102 град/см, то Εy ~ 10-2 В/см.
q⊥ залежить від температури і магнітного поля і при зміні цих величин може навіть міняти знак.
Знак q⊥ не залежить від знаку носіїв заряду.
Слайд 25
Поперечний термомагнітний ефект Нернста-Етінгсгаузена.
Даний ефект виникає по
тій же причині, що і ефект Хола, тобто в
результаті відхилення потоку заряджених частинок силою Лоренца. Відмінність, однак, полягає в тім, що при ефекті Хола направлений потік частинок виникає в результаті їх дрейфу в електричному полі, а в даному випадку – в результаті дифузії.
Слайд 26
8. Ефект Рігі-Ледюка.
Поперечний термомагнітний ефект Рігі-Ледюка.
В провіднику, в
якому є градієнт температури, при включенні магнітного поля зявляється
також поперечна (по відношенню до початкового теплового потоку і напрямку В) різниця температур.
dT/dy = S Bz dt/dz
де S - постійна Рігі-Ледюка, що характеризує властивості даної речовини.
Ефект Рігі-Ледюка пов'язаний з тим, дифундуючи носії заряду переносять з собою тепло (теплопровідність). Без магнітного поля потік тепла направлений від гарячого кінця до холодного, тобто паралельно -∇xТ. В магнітному полі потоки дифузії і тепла повертаються силою Лоренца на деякий кут. Тому виникає складова теплового потоку вздовж осі Y, що і приводить до появи складової градієнта температури -∇yТ. Так як сили Лоренца при даному напрямку дифузії залежать від знаку заряджений частинок, то кут повороту теплового потоку, а значить і постійна мають різні знаки для позитивних і негативних носіїв заряду.
Слайд 27
9. Повздовжні термомагнітні ефекти.
Повздовжні термомагнітні ефекти:
- поздовжній ефект
Нернста-Етінгсгаузена-зміна термоерс в поперечному магнітному полі;
- поздовжній ефект Рігі-Ледюка
– зміна теплопровідності в магнітному полі.
Теплообмін з оточуючим середовищем
Ізотермічний – поперечні градієнти температур рівні 0;
Адіабатичний – поперечні потоки тепла рівні 0.
Величини різних кінетичних коефіцієнтів – електропровідності, постійної Хола, термоерс та ін. – суттєво залежать від властивостей рухливих носіїв заряду: їх заряду, маси, енергетичного спектру в кристалі, а також від особливостей їх взаємодії з кристалічною граткою.