- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Лабораторная работа: Измерение плотности бруска различными способами
Содержание
- 2. Оборудование: деревянный брусок, миллиметровая бумага, линейка, монетки
- 3. Теория Плотность вещества по определению
- 4. В нашем случае объём
- 5. Массу бруска можно измерить
- 6. Размещая грузик на одном
- 7. Принимая, что брусок однороден,
- 8. Ход измеренийЛинейкой измеряем длину ℓ, ширину b
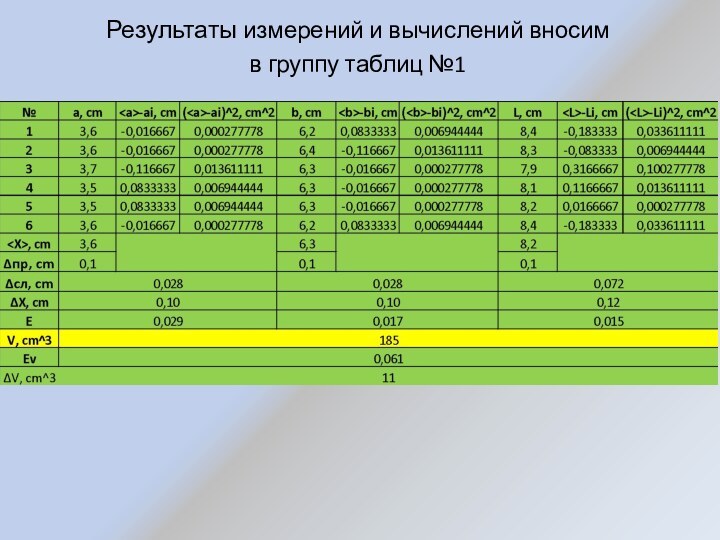
- 9. Результаты измерений и вычислений вносим в группу таблиц №1
- 11. Обработка результатов измерений Для
- 12. Разделив значение абсолютной погрешности
- 13. На примере объёма бруска получаем:∆слa = √∑
- 14. Записываем ответ в виде:V = ( ±
- 15. Массу бруска можно рассчитать
- 16. Так как вес в
- 17. Ход измеренийПриклеиваем полоску миллиметровой бумаги на сосуд
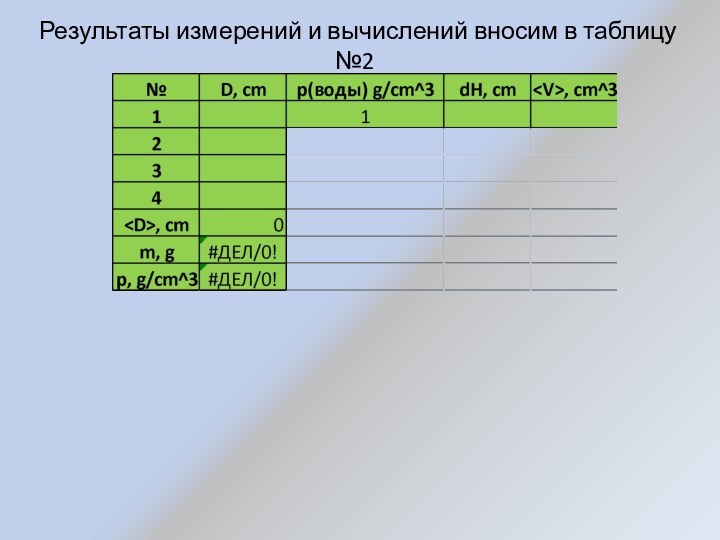
- 18. Результаты измерений и вычислений вносим в таблицу №2
- 19. Скачать презентацию
- 20. Похожие презентации
Оборудование: деревянный брусок, миллиметровая бумага, линейка, монетки известной массы, сосуд с водой, салфетки, скотч.Цели работы: 1. Измерить плотность бруска двумя различными способами. 2. Изучить способы вычисления погрешности измерений.













Слайд 2 Оборудование: деревянный брусок, миллиметровая бумага, линейка, монетки известной
массы, сосуд с водой, салфетки, скотч.
плотность бруска двумя различными способами. 2. Изучить способы вычисления погрешности измерений.
Слайд 3
Теория
Плотность вещества по определению –
масса его единичного объёма. Вычисляется плотность как отношение массы
тела к его объёму.ρ = m/V
Где: ρ – плотность [г/см3]
m – масса [г]
V – объём [см3]
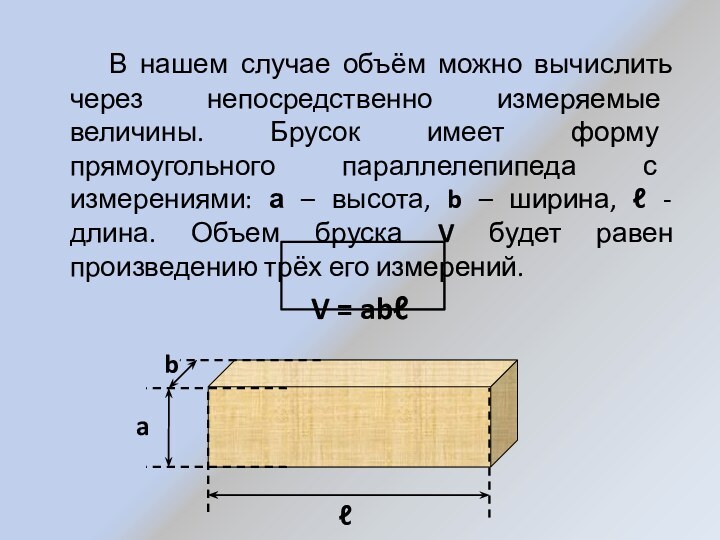
Слайд 4 В нашем случае объём можно
вычислить через непосредственно измеряемые величины. Брусок имеет форму прямоугольного
параллелепипеда с измерениями: а – высота, b – ширина, ℓ - длина. Объем бруска V будет равен произведению трёх его измерений.V = abℓ
a
b
ℓ
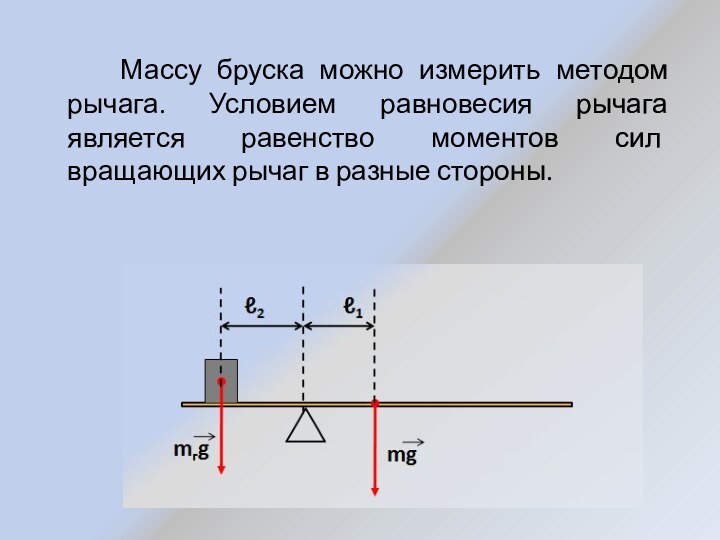
Слайд 5 Массу бруска можно измерить методом
рычага. Условием равновесия рычага является равенство моментов сил вращающих
рычаг в разные стороны.Слайд 6 Размещая грузик на одном из
концов бруска и выдвигая его за край стола, можно
найти такое положение, когда точка приложения силы нормальной реакции практически совпадёт с вертикалью, проходящей через край стола. То есть брусок окажется в неустойчивом положении на краю стола. При этом равенство моментов сил, действующих на брусок запишется в виде:mgℓ1 = mгgℓ2
Где: m – масса бруска [г]
ℓ1 - плечо силы тяжести,
действующей на брусок [см]
mг - известная масса грузика [г]
ℓ2 - плечо силы тяжести, действующей на грузик [см]
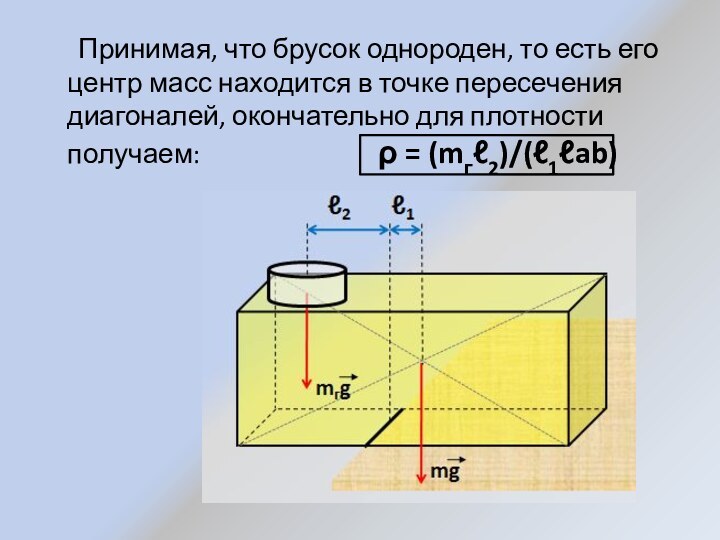
Слайд 7 Принимая, что брусок однороден, то
есть его центр масс находится в точке пересечения диагоналей,
окончательно для плотности получаем: ρ = (mгℓ2)/(ℓ1ℓab)
Слайд 8
Ход измерений
Линейкой измеряем длину ℓ, ширину b и
высоту а бруска в 6 местах. Находим среднее арифметическое
каждого измерения. Вычисляем объём бруска по формуле: V = <ℓ>.При помощи канцелярской кнопки прикрепляем нить с грузиком массы mг = 20 г к торцу бруска, имеющему наименьшую площадь.
Осторожно выдвигаем конец бруска с грузиком за край стола, до того момента, как брусок окажется уравновешенным в неустойчивом положении. Измеряем длину ℓ0 оставшейся на столе части бруска, при помощи линейки, в двух разных положениях с двух разных сторон. Находим среднее арифметическое полученного значения длины.
Вычисляем плечи сил mg и mгg по формулам ℓ1 = <ℓ0> - <ℓ>/2 и ℓ2 = <ℓ> - <ℓ0> соответственно.
Вычисляем массу бруска по формуле: m = mгℓ2/ℓ1.
Вычисляем плотность бруска по формуле: ρ = m/V.
Слайд 11
Обработка результатов измерений
Для каждого
прямого измерения находим отклонение от среднего значения величины -Xi
и квадрат этого отклонения (∆сл = √∑ (
Извлекая квадратный корень из суммы квадратов случайной погрешности ∆сл2 и приборной погрешности ∆пр2, равной цене наименьшего деления прибора (для линейки или миллиметровой бумаги: 0,1 см), находим значение абсолютной погрешности прямого измерения ∆X.
∆X = √(∆сл2 + ∆пр2)
Слайд 12 Разделив значение абсолютной погрешности ∆X
на среднее значение измеряемой величины получаем значение относительной
погрешности измерения E.E = ∆X/
Для вычисления относительной погрешности вычисляемой величины, получаемой умножением или делением измеряемых величин необходимо сложить все относительные погрешности измеряемых величин, входящих в формулу вычисляемой величины.
Для вычисления абсолютной погрешности вычисляемой величины, получаемой сложением или вычитанием измеряемых величин, необходимо сложить абсолютные погрешности этих величин.
Для вычисления же абсолютной погрешности вычисляемой величины необходимо умножить относительную погрешность, на значение данной величины, получаемое при вычислении её из средних значений измеряемых величин.
Слайд 13
На примере объёма бруска получаем:
∆слa = √∑ (-ai)2/6
∆прa
= 0,1 см
∆a = √ (∆сл2a + ∆пр2a )
Ea
= ∆a/ Аналогично для величин b и ℓ.
Далее рассчитываем относительную погрешность объёма бруска.
Ev = Ea+Eb+Eℓ
Затем находим абсолютную погрешность объёма бруска:
∆V = VEv
Слайд 14
Записываем ответ в виде:
V = ( ± ∆V)
г/см3 при Ev =_%
При вычислениях
все величины округляем до того наименьшего количества значащих цифр, которое присутствует в измеряемых величинах (для бруска значащих цифры будет две).При записи ответа абсолютная погрешность округляется до одной значащей цифры в большую сторону, а среднее значение округляется до такого, при котором погрешность приходится лишь на последнюю значащую цифру.
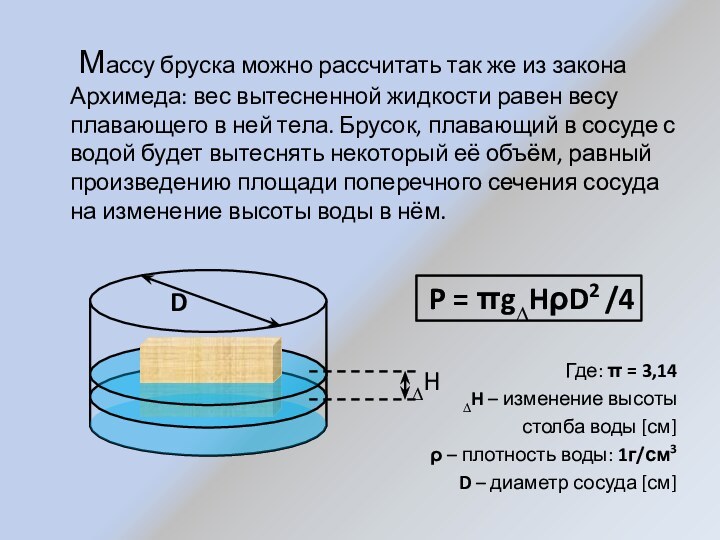
Слайд 15 Массу бруска можно рассчитать так
же из закона Архимеда: вес вытесненной жидкости равен весу
плавающего в ней тела. Брусок, плавающий в сосуде с водой будет вытеснять некоторый её объём, равный произведению площади поперечного сечения сосуда на изменение высоты воды в нём.Где: π = 3,14
∆H – изменение высоты
столба воды [см]
ρ – плотность воды: 1г/см3
D – диаметр сосуда [см]
∆H
D
P = πg∆HρD2 /4
Слайд 16 Так как вес в состоянии
покоя есть произведение массы тела на ускорение свободного падения,
окончательно для массы бруска получаем:m = P/g
m = π∆HρD2 /4
А для плотности:
ρ = π∆HρD2 /4abℓ
Слайд 17
Ход измерений
Приклеиваем полоску миллиметровой бумаги на сосуд с
водой.
Отмечаем на бумаге положение первоначального уровня воды. Опускаем брусок
в сосуд и дожидаемся пока поверхность воды не выровняется. Отмечаем на бумаге высоту нового уровня воды.Находим изменение ∆H уровня воды в сосуде.
Измеряем диаметр сосуда в четырёх местах и находим среднее арифметическое измерений
Рассчитываем массу бруска по формуле: m = π∆Hρ






![[Методическая разработка] Лабораторной работы методическая разработка](/img/tmb/9/861366/53c9f09dc7e9b8ee8527326eded87272-210x.jpg)






















