Презентация на тему Механические характеристики материалов

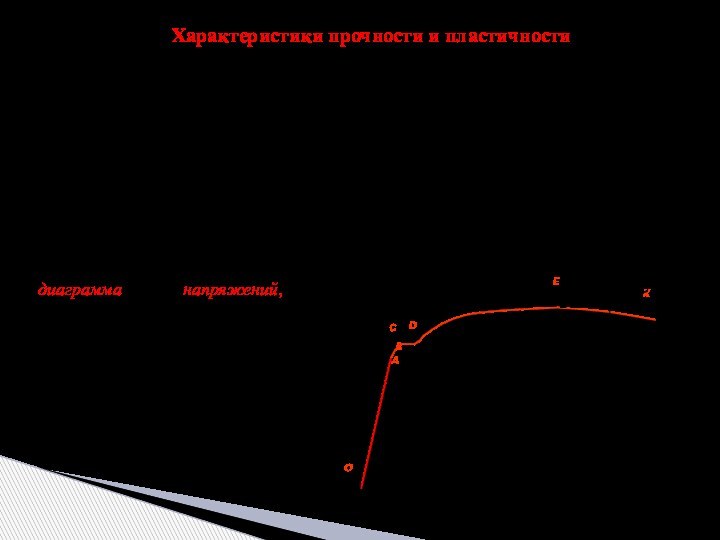
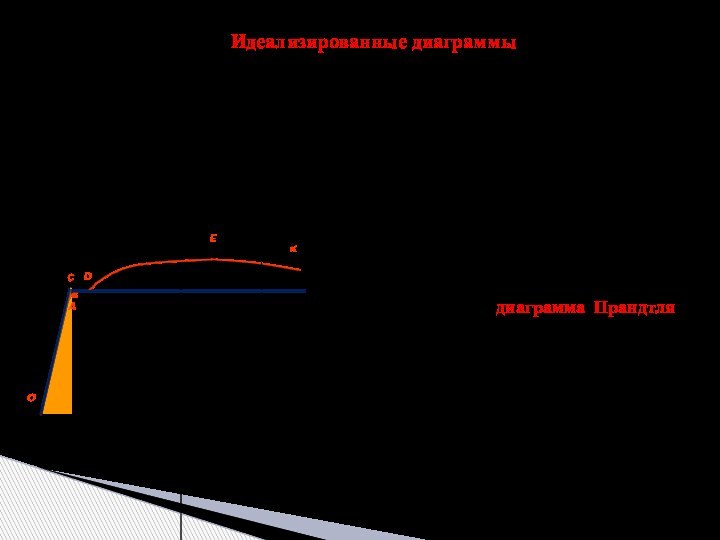
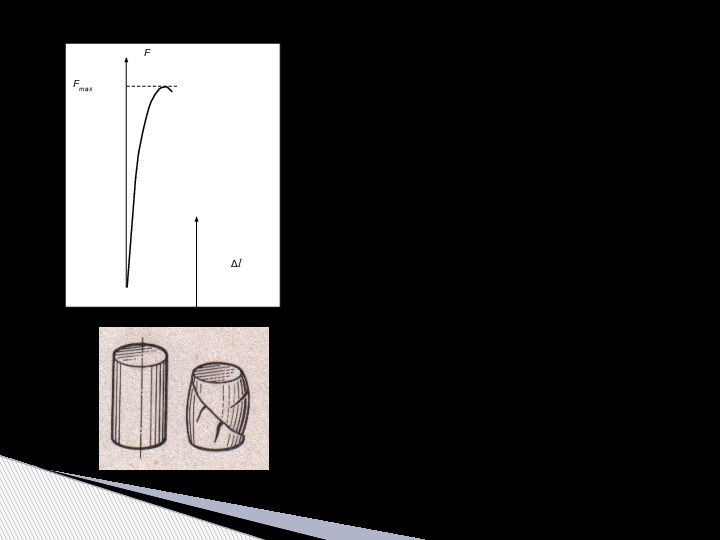
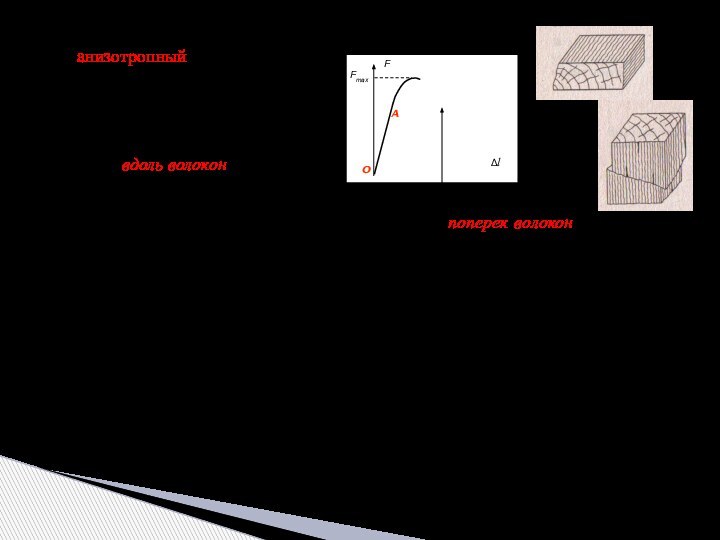
прочностные и деформационные свойства материалов, которые определяют экспериментально на

специальных испытательных машинах. Из всех прочих свойств (твердость, сопротивляемость ударным нагрузкам, противодействие высоким или низким температурам и т.п.) основными являются сопротивление на растяжение и сжатие, дающие наибольшую и важнейшую информацию о механических свойствах металлов.

Испытание на растяжение – проводят на разрывных или универсальных машинах, имеющих специальные захваты для передачи усилия. Используются стандартные образцы специальной формы (l0 – длина рабочей части, l0/d0 = 5 – короткие, l0/d0 = 10 – длинные):

отношением высоты к диаметру h/d = 1,5 - 3.
Образцы

устанавливаются на опорную поверхность
с использованием смазки для ослабления влияния сил трения.

Все машины снабжены устройством для автоматической записи в определенном масштабе диаграммы-графика зависи-мости величины удлинения образца от растягивающей силы.
Современные машины компьюте-ризированы и имеют средства управления процессом нагружения по различным задаваемым программам, вывода данных на экран и сохранения их в файлах для последующей обработки.

диаграммой пластичных материалов является диаграмма растяжения низкоуглеродистой стали (

0,25% С):

2. Далее (AB, до Fуп) деформации начинают расти чуть быстрее и не линейно, но остаются малыми и упругими (исчезающими после снятия нагрузки).

3. При дальнейшем нагружении (BС, до Fт) криволинейная часть переходит в горизонтальную площадку CD, на которой деформации растут без увеличения нагрузки (текучесть). Зона BCD – зона общей текучести.

4. При дальнейшем нагружении (DE, до Fмакс) изменяется структура металла и материал вновь может воспринимать возрастание нагрузки (упрочнение) вплоть до максимальной.

5. Далее (EK, до Fк) в наиболее слабом месте возникает и развивается локальное уменьшение поперечного сечения (шейка). Зона EK – зона местной текучести.

В точке K образец внезапно разрушается
с резким ударным звуком, но без световых эффектов.

1. В начальной стадии (OA, до Fпц) нагружения удлинение растет прямопропорционально величине нагрузки (на этой стадии справедлив закон Гука);

может непосредственно характеризовать прочность и пластичность материала, поскольку нагрузка

зависит от площади поперечного сечения образца, а удлинение – от базовой его длины. Для получения объективных механических характеристик материала, не зависящих от сечения и длины образца, необходимо перейти к напряжениям и относительным удлинениям. Для этого нагрузка делится на начальную или текущую площадь поперечного сечения образца, а по оси абсцисс откладывается соответствующее относительное удлинение для каждой из характерных точек.

Характеристики прочности и пластичности

В результате получается диаграмма напряжений, подобная диаграмме растяжения.

В этой диаграмме характерные точки определяют механические свойства материала.

которого существует пропорциональная (прямая) зависимость между нагрузкой и деформацией

(для Ст3 - σпц =195-200 МПа).

Механические свойства материала:

2. Предел упругости σуп – наибольшее напряжение, при котором в материале не обнаруживается признаков пластической (остаточной) деформации (для Ст3 - σуп =205-210 МПа).

3. Предел текучести σт – наименьшее напряжение, при котором образец деформируется без заметного увеличения растягивающей нагрузки (для Ст3 - σт =220-250 МПа).

напряжение, соответствующее наибольшей нагрузке, предшествующей разрушению образца.
(для Ст3 -

σв =370-470 МПа).

5. Истинный предел прочности или истинное сопротивление разрыву σи – напряжение, соответствующее разрушающей силе FK, вычисленное для площади поперечного сечения образца в месте разрыва A1 (для Ст3 - σв =900-1000 МПа). Поскольку на участке EK образуется шейка и площадь поперечного сечения быстро уменьшается, напряжение увеличивается (EK1) при регистрируемом падении усилия.

Механизм разрушения: в области шейки образуются мелкие продольные трещины, которые затем сливаются в одну центральную трещину, перпендикулярную оси растяжения, далее трещина распространяется к поверхности шейки, разворачиваясь примерно на 450, и при выходе на поверхность образует коническую часть излома.

В результате получается поверхность излома в виде “конуса” и “чашечки”. Стадия образования конической поверхности показывает, что материал в вершине трещины начинает разрушаться по механизму скольжения (по площадкам максимальных касательных напряжений), характерному для хрупких материалов.

его сопротивлении переменным динамическим нагрузкам, а также технологическим свойством

при его обработке (штамповка и др.).
К характеристикам пластичности относятся:

Характеристики пластичности

Δl

dΔl

Относительное удлинение после разрыва δ (%) – отношение приращения расчетной длины образца после разрыва к ее первоначальному значению (для Ст3 - δ = 25-27 %).

2. Относительное сужение после разрыва ψ (%) – отношение уменьшения площади поперечного сечения образца в месте разрыва к начальной площади поперечного сечения (для Ст3 - ψ =60-70 %).

диаграммы растяжения:
Полная удельная работа, совершенная для разрыва образца, равна

площади диаграммы растяжения

упругой деформации:

свойство материала восстанавливать свои первоначальные форму и размеры после

снятия действующих сил.
Пластичность – свойство материала получать значительные остаточные деформации до разрушения.
Хрупкость – свойство материала разрушаться при небольших деформациях.
Твердость – свойство материала сопротивляться продавливанию в него других тел под действием внешних сил.

Модуль упругости материала (модуль Юнга) - Е (Па), коэффициент, устанавливающий линейный закон зависимости между напряжением (до предела пропорциональности) и относительным удлинением, из диаграммы растяжения определяется по формуле:

поперечной деформации μ.

– коэффициент поперечной деформации (коэффициент Пуассона),

постоянная величина для данного материала;

– относительная линейная поперечная деформация (сужение);

– относительная линейная продольная деформация.

абсолютный сдвиг образца;
γ – угол сдвига (относительный сдвиг),

– модуль упругости при сдвиге

γ

γ

– закон Гука при сдвиге

задачи, в которой необходимо иметь аналитическую зависимость между напряжениями

и деформациями. Такую зависимость, представляемой полученной экспериментально диаграммой напряжений, сложно получить в аналитическом виде и использовать в расчетах.

В связи с этим используются упрощенные (идеализированные) диаграммы, отражающие основные закономерности. В частности, для пластичных материалов часто применяется диаграмма Прандтля, состоящая всего из двух прямолинейных участков.
Как видно, диаграмма Прандтля распространяет зону действия закона Гука до предела текучести, после чего предполагается (задается), что материал испытывает далее текучесть вплоть до разрушения.

Идеализированные диаграммы

прямолинейным ( до точки A) и совпадает с аналогичным

участком диаграммы растяжения. Это свидетельствует о том, что модуль упругости у стали можно принимать одинаковым при растяжении и сжатии. Нелинейный участок до площадки текучести также совпадает с подобным участком на диаграмме растяжения. Значения предела пропорциональности и предела текучести при растяжении и сжатии практически одинаковы. Площадка текучести при сжатии выражена очень слабо и после нее кривая уходит все более круто вверх вследствие развития значительных пластических деформаций, приводящих к увеличению площади поперечного сечения. Образец сплющивается принимая бочкообразную форму. На этом испытания заканчивают, т.к. образец разрушить не удастся, не удается определить и предел прочности.

Диаграммы сжатия различных материалов

линейную зависимость, на этом участке форма и размеры образца

меняются незначительно. При приближении к максимальной нагрузке кривая становится более пологой и образец принимает слегка бочкообразную форму. При достижении нагрузкой наибольшего значения появляются трещины под углом примерно 450 и наступает разрушение по площадкам с наибольшими касательными напряжениями (хрупкое разрушение).
Другие хрупкие материалы (камень, бетон) имеют подобную диаграмму и такой же характер разрушения. Хрупкие материалы сопротивляются сжатию значительно лучше, чем растяжению, например, предел прочности серого чугуна на сжатие 560-900 МПа, а на растяжение – 120-190 Мпа.

при сжатии зависит от расположения волокон относительно направления сжимающей

силы.
При сжатии вдоль волокон на участке OA древесина работает почти упруго, деформации растут пропорционально увеличению сжимающей силы. Далее деформации начинают расти более быстро, чем усилие, вследствие возникновения пластических деформаций в отдельных волокнах.
Разрушение происходит при максимальной нагрузке в результате потери местной устойчивости ряда волокон, сопровождаемой сдвигом с образованием продольных трещин.

При сжатии поперек волокон на участке OB древесина работает почти упруго, деформации растут пропорционально увеличению сжимающей силы. Далее деформации начинают расти очень быстро при малом увеличении силы, вследствие уплотнения (спрессовывания) отдельных волокон. При наличии сучков и других пороков (трещин) образец может разрушиться раскалыванием.
Разрушающая нагрузка определяется условно при достижении деформации сжатия, при которой высота образца уменьшается на треть исходной высоты .