- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Механика движения
Содержание
- 2. Список учебной литературыИ.В. Савельев. Курс общей физики.
- 3. Структура механикиФизика – наука о наиболее общих
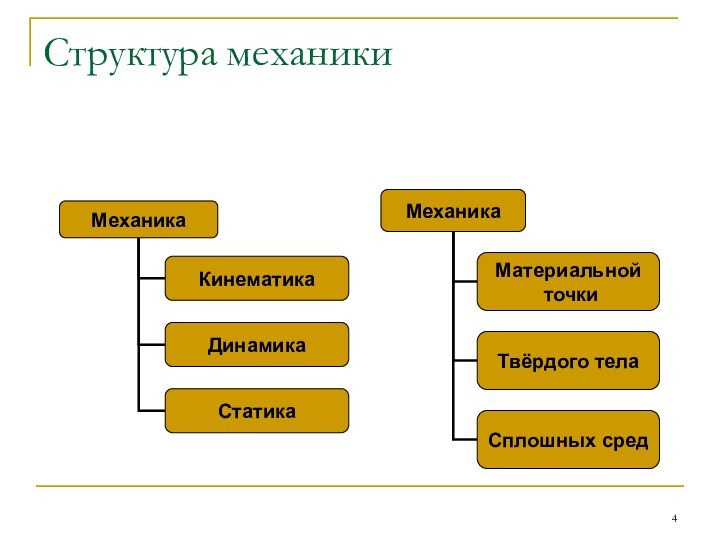
- 4. Структура механики
- 5. Основные понятия механикиОсновная задача механики – зная
- 6. Основные понятия механикиМеханическая система – совокупность тел,
- 7. Основные понятия механикиПоступательное движение – такое, при
- 8. Основные понятия механикиСистема координат состоит из осей,
- 9. Основные понятия механикиПеремещение – это вектор, проведённый от начальной точки движения к конечной (r1,2)Скорость: (1) (2) (3)
- 10. Основные понятия механикиУскорение: (4)В координатном представлении:
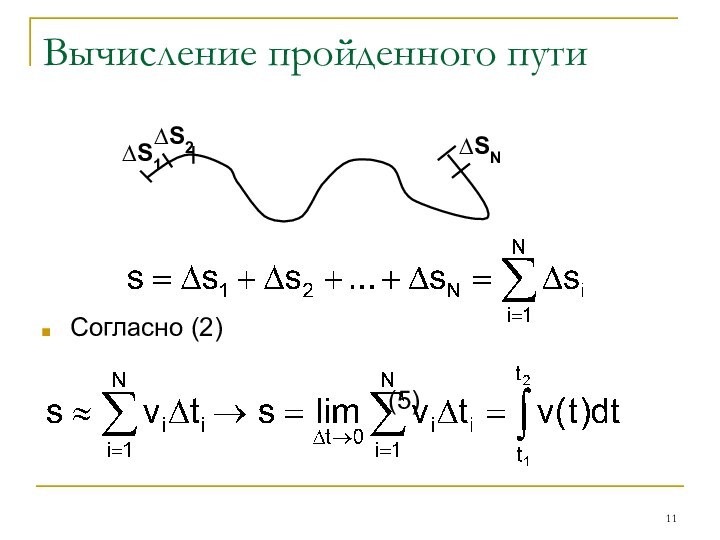
- 11. Вычисление пройденного пути Согласно (2) (5)
- 12. Вычисление перемещенияЕсли в (5) взять интеграл не
- 13. Средняя скоростьПо определению, средняя скорость равна: (7)Если скорость движения изменялась скачками, то (7) перейдёт в: (8)
- 14. Разложение ускорения на нормальную и тангенциальную компонентыВведём
- 15. Разложение ускорения на нормальную и тангенциальную компонентыМожно показать, что производная вектора eτ перпендикулярна к траектории движения
- 16. Разложение ускорения на нормальную и тангенциальную компонентыТаким
- 17. Разложение ускорения на нормальную и тангенциальную компоненты
- 18. Кинематика прямолинейного движенияПрямолинейное движение с постоянным ускорением можно описать с помощью уравнений кинематики прямолинейного движения (10)
- 19. Кинематика прямолинейного движенияВ уравнениях (10) t –
- 20. Кинематика вращательного движенияВращательное движение характеризуют угловыми величинами,
- 21. Кинематика вращательного движенияУгловая скорость направлена вдоль оси
- 22. Кинематика вращательного движенияПри ω=const вращение называют равномернымРавномерное вращение можно характеризовать периодом Т=2π/ω и частотой υ=1/Т ω=2π/Т=2πυ
- 23. Кинематика вращательного движенияУгловое ускорение: (12)Необходимо учитывать, что угловая
- 24. Связь между угловыми и линейными величинамиСвязь между
- 25. Кинематика вращательного движенияУравнения кинематики равноускоренного вращательного движения вокруг фиксированной оси имеют вид: (13)
- 26. Некоторые сведения о векторахВектором будем называть величину,
- 27. Некоторые сведения о векторахДля векторов определены операции
- 28. Некоторые сведения о векторахКоординатное представление векторов. Если
- 29. Некоторые сведения о векторахЗапись вектора в координатном представлении:Сумма векторов определяется суммами их соответствующих координат:
- 30. Некоторые сведения о векторахМодуль суммы двух векторов
- 31. Некоторые сведения о векторахВ координатном представлении векторное произведение можно записать в виде определителя:
- 32. Скачать презентацию
- 33. Похожие презентации
Список учебной литературыИ.В. Савельев. Курс общей физики. Т.1. Механика и молекулярная физикаТ.И. Трофимова. Курс физикиМеханика, колебания и волны в упругих средах. Сборник задач по физике под ред. Д.С. Фалеева. ДВГУПС, 2004

























Слайд 2
Список учебной литературы
И.В. Савельев. Курс общей физики. Т.1.
Механика и молекулярная физика
волны в упругих средах. Сборник задач по физике под ред. Д.С. Фалеева. ДВГУПС, 2004
Слайд 3
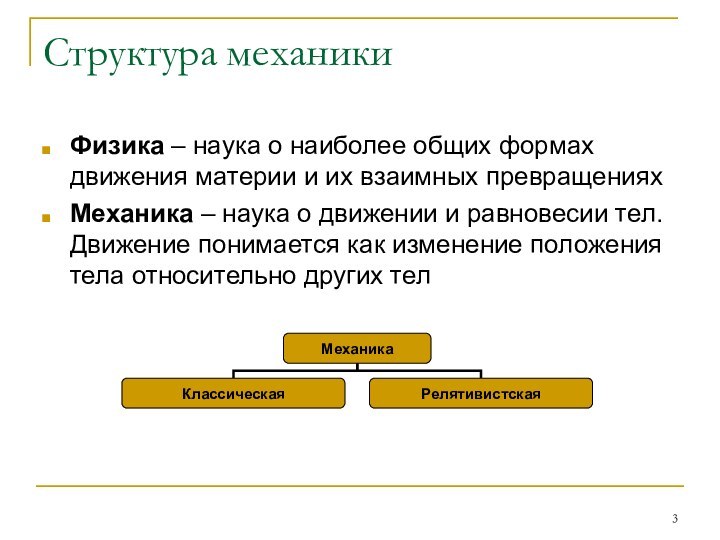
Структура механики
Физика – наука о наиболее общих формах
движения материи и их взаимных превращениях
Механика – наука о
движении и равновесии тел. Движение понимается как изменение положения тела относительно других тел
Слайд 5
Основные понятия механики
Основная задача механики – зная состояние
системы в начальный момент времени и законы, управляющие движением,
определить состояние системы во все последующие моменты времени. Эта задача не может быть решена точноКинематика – это раздел физики, посвящённый изучению движения тел. При этом причины движения не рассматриваются
Слайд 6
Основные понятия механики
Механическая система – совокупность тел, выделенная
для рассмотрения
Система отсчёта – совокупность неподвижных друг относительно друга
тел, по отношению к которым рассматривается движение, и часыМатериальная точка – тело, размерами которого можно пренебречь в условиях данной задачи
Абсолютно твёрдое тело – это тело, деформациями которого можно пренебречь
Слайд 7
Основные понятия механики
Поступательное движение – такое, при котором
любая прямая, связанная с телом перемещается параллельно самой себе
Вращательное
движение – такое, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения
Слайд 8
Основные понятия механики
Система координат состоит из осей, для
определения пространственных координат тела и часов
Траектория – это линия,
которую описывает некоторая материальная точка в процессе движенияПуть – это расстояние между двумя точками, измеренное вдоль траектории движения
Слайд 9
Основные понятия механики
Перемещение – это вектор, проведённый от
начальной точки движения к конечной (r1,2)
Скорость:
(1)
(2)
(3)
Слайд 12
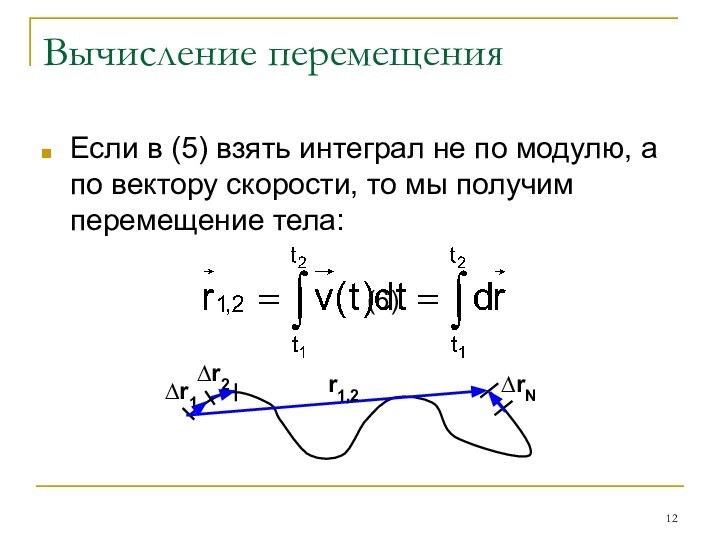
Вычисление перемещения
Если в (5) взять интеграл не по
модулю, а по вектору скорости, то мы получим перемещение
тела:(6)
Слайд 13
Средняя скорость
По определению, средняя скорость равна:
(7)
Если скорость движения
изменялась скачками, то (7) перейдёт в:
(8)
Слайд 14
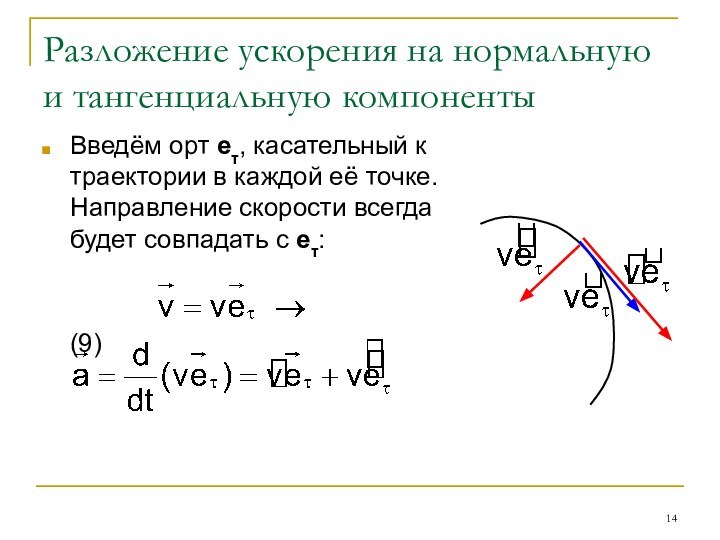
Разложение ускорения на нормальную и тангенциальную компоненты
Введём орт
eτ, касательный к траектории в каждой её точке. Направление
скорости всегда будет совпадать с eτ:(9)
Слайд 15
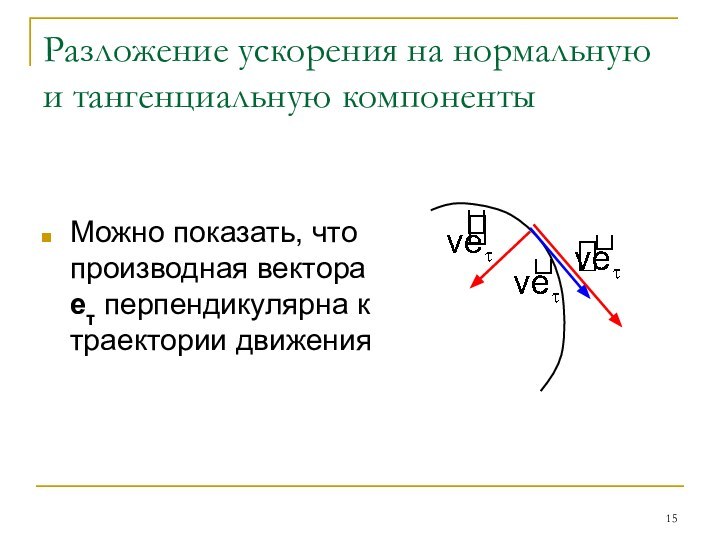
Разложение ускорения на нормальную и тангенциальную компоненты
Можно показать,
что производная вектора eτ перпендикулярна к траектории движения
Слайд 16
Разложение ускорения на нормальную и тангенциальную компоненты
Таким образом,
мы разложили вектор ускорения на две составляющие:
вдоль траектории
движения перпендикулярно к траектории движения
и тем самым показали, что любое движение можно представить как суперпозицию поступательного и вращательного движений
Слайд 18
Кинематика прямолинейного движения
Прямолинейное движение с постоянным ускорением можно
описать с помощью уравнений кинематики прямолинейного движения
(10)
Слайд 19
Кинематика прямолинейного движения
В уравнениях (10) t – время
движения, х – координата, вдоль которой происходит движение, х0
– её начальное значение (в момент t=0), vx – скорость движения, v0x – её начальное значение, ax – ускорениеЕсли направление движения не совпадает с направлением какой-либо координатной оси, то вместо каждого из уравнений (10) надо записать три подобных уравнения для проекций координаты и скорости на оси
Слайд 20
Кинематика вращательного движения
Вращательное движение характеризуют угловыми величинами, имеющими
линейные аналоги
Углы поворота вокруг трёх различных осей характеризуют пространственное
положение точкиУгловая скорость характеризует скорость изменения положения точки
Слайд 21
Кинематика вращательного движения
Угловая скорость направлена вдоль оси вращения
(11)
Модуль
вектора ϕ равен углу поворота, а направление определяется по
правилу правого винтаУгловая скорость определяется в радианах в секунду [рад/с]
Слайд 22
Кинематика вращательного движения
При ω=const вращение называют равномерным
Равномерное вращение
можно характеризовать периодом
Т=2π/ω
и частотой
υ=1/Т
ω=2π/Т=2πυ
Слайд 23
Кинематика вращательного движения
Угловое ускорение:
(12)
Необходимо учитывать, что угловая скорость
может изменяться как по величине, так и по направлению
Слайд 24
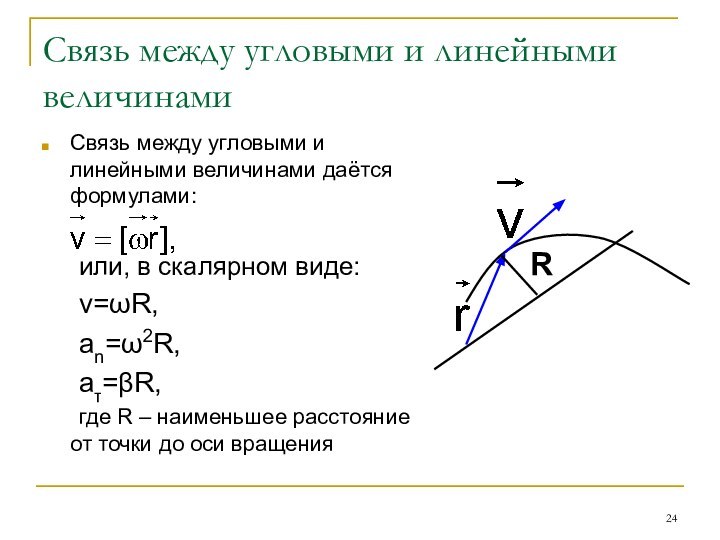
Связь между угловыми и линейными величинами
Связь между угловыми
и линейными величинами даётся формулами:
или, в скалярном виде:
v=ωR,
an=ω2R,
aτ=βR,
где R
– наименьшее расстояние от точки до оси вращенияR
Слайд 25
Кинематика вращательного движения
Уравнения кинематики равноускоренного вращательного движения вокруг
фиксированной оси имеют вид:
(13)
Слайд 26
Некоторые сведения о векторах
Вектором будем называть величину, характеризующуюся
численным значением (модулем) и направлением в пространстве, для которой
задан закон сложения (правило параллелограмма)Различают коллинеарные, компланарные, свободные, скользящие и связанные векторы
Слайд 27
Некоторые сведения о векторах
Для векторов определены операции сложения,
умножения на число, скалярного и векторного произведений
Скалярное произведение двух
векторов – это число:где α - угол между векторами a и b





























