- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Модели негауссовых случайных блужданий с конечной дисперсией
Содержание
- 2. 1. Задача о случайных блужданиях (формулировка Пирсона)Задача
- 3. 2. Задача о случайных блужданияхЗадача о случайных
- 4. 3. ДиффузияЭкспериментальные наблюдения: диффузия частичек угольной пыли
- 5. 4. Случайные блуждания с непрерывным временем (CTRW)Данная
- 6. 5. Случайные блуждания (случай отсутствия второго и
- 7. 6. Распределение ЛевиСвойства устойчивого симметричного распределения Леви:
- 8. 7. Распределения Леви в физике и других
- 9. 8. Случайные блуждания (случай отсутствия моментов закона
- 10. 9. Промежуточные выводыВведение закона прыжка вида: позволяет единым
- 11. 10. Эмпирически наблюдаемые негауссовы случайные блужданияДискретные временные
- 12. 11. Статистические характеристики финансовых временных рядовДискретные временные
- 13. 12. Определение минимального масштаба процессаЭмпирические данные позволяют
- 14. 13. Применение модели «усеченных» блужданий Леви для
- 15. 14. Модификация модели Обнаружено эмпирическое кумулятивное распределение
- 16. 15. Сравнение результатов модели и эмпирических данных.Если
- 17. 16. Выводы Введение закона прыжка позволяет единым
- 18. Публикации1. Видов П.В., Романовский М.Ю., Доходность активов
- 19. Спасибо за внимание!
- 20. Скачать презентацию
- 21. Похожие презентации










Слайд 3
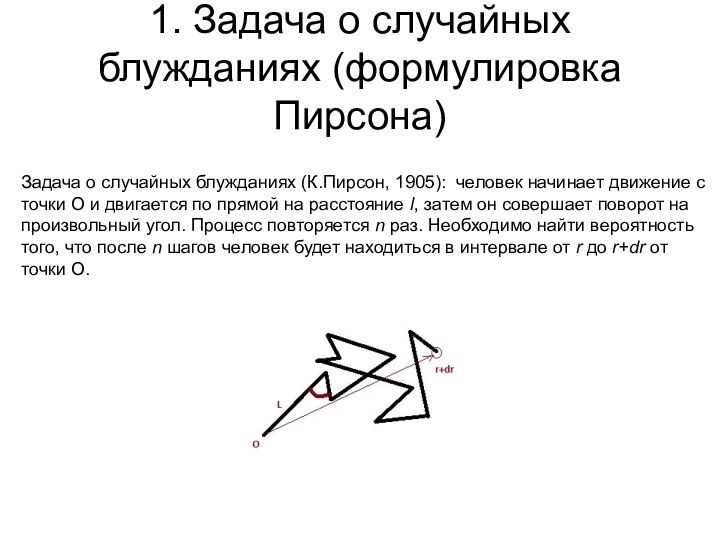
2. Задача о случайных блужданиях
Задача о случайных блужданиях:
нужно найти плотность вероятности того, что частица, испытав N
прыжков в пространстве некоторой размерности G окажется в интервалеКаждый i-ы прыжок может быть произведен в интервал длин
с вероятностью
*Chandrasekhar S Rev.Mod.Phys. 15 1 (1943).
Важнейшим требованием для решения является наличие всех моментов закона прыжка
(1)
(2)
(3)
(4)
(5)
Слайд 4
3. Диффузия
Экспериментальные наблюдения:
диффузия частичек угольной пыли
на
поверхности спирта (Я.Ингенхоуц, 1785)
движения пыльцы в жидкости (Р.
Броун, 1827) Математические результаты:
К.Винер предположил, что движение броуновской частицы является следствием ее соударений с молекулами жидкости (1863)
А.Эйнштейн получил уравнение диффузии
Хаотическое движение молекул жидкости можно представить как случайные блуждания с характерной длиной блуждания и временем . Нас интересует вид функции , которая определяет плотность вероятности того, что частица будет находиться в положении в момент времени при стремлении величин:
Слайд 5
4. Случайные блуждания с непрерывным временем (CTRW)
Данная модель
предполагает, что прыжки или блуждания происходят в независимые случайные
моменты времени, при этом вероятность того, что следующий прыжок произойдет через промежуток времени от до определяется плотностью распределенияВ случае если характерное время между прыжками
конечно, то есть интеграл сходится, можно утверждать, что время, необходимое для совершения N прыжков, равно NT. Таким образом, можно заменить в дискретной задаче N на непрерывное время t/T.
Условная плотность распределения вероятности нахождения частицы в точке x в момент времени t определяется как:
Слайд 6 5. Случайные блуждания (случай отсутствия второго и более
высоких моментов закона прыжка)
Закон элементарного прыжка, не дающий всех
конечных моментов, но обладающий нормировкой: 3/2>β>1/2 , z – характерная длина прыжка
Большие флуктуации могут возникать посредствам одного прыжка (R=r при N=1)
Функция W1(R) - самоподобна
Медленно спадающая асимптотика, значительное количество больших флуктуаций
- Распределение Леви
Слайд 7
6. Распределение Леви
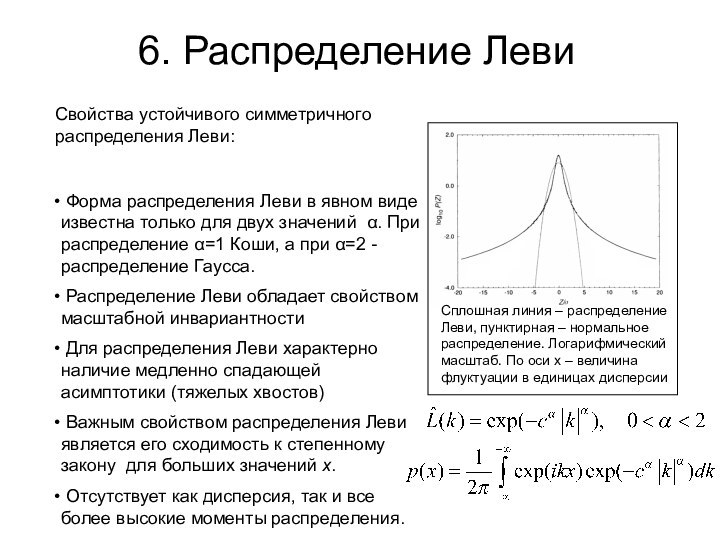
Свойства устойчивого симметричного распределения Леви:
Форма
распределения Леви в явном виде известна только для двух
значений α. При распределение α=1 Коши, а при α=2 - распределение Гаусса.Распределение Леви обладает свойством масштабной инвариантности
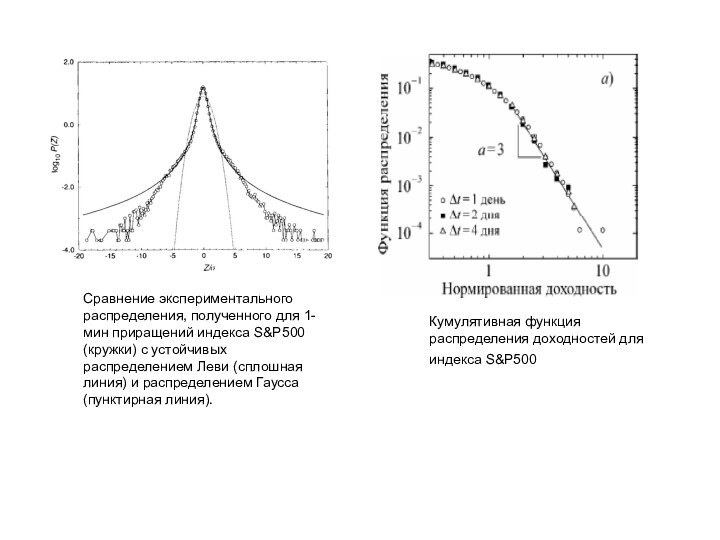
Для распределения Леви характерно наличие медленно спадающей асимптотики (тяжелых хвостов)
Важным свойством распределения Леви является его сходимость к степенному закону для больших значений x.
Отсутствует как дисперсия, так и все более высокие моменты распределения.
Сплошная линия – распределение Леви, пунктирная – нормальное распределение. Логарифмический масштаб. По оси x – величина флуктуации в единицах дисперсии
Слайд 8 7. Распределения Леви в физике и других областях
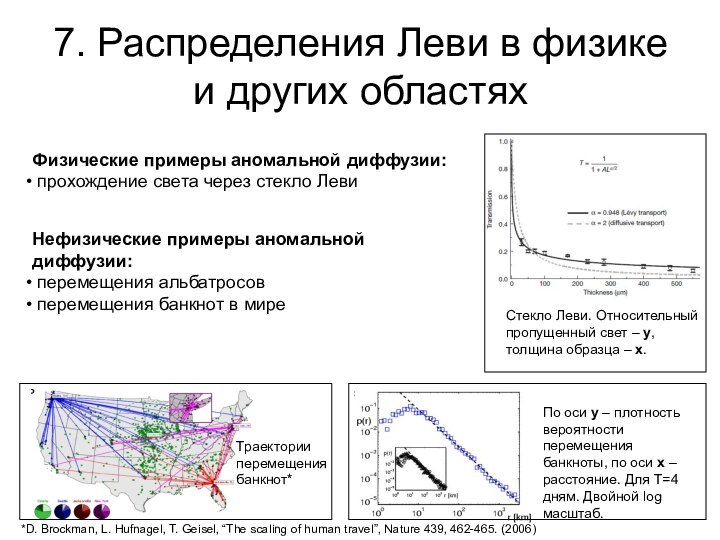
Физические примеры аномальной диффузии:
прохождение света через стекло Леви
Нефизические
примеры аномальной диффузии:перемещения альбатросов
перемещения банкнот в мире
Траектории перемещения банкнот*
По оси y – плотность вероятности перемещения банкноты, по оси x – расстояние. Для T=4 дням. Двойной log масштаб.
*D. Brockman, L. Hufnagel, T. Geisel, “The scaling of human travel”, Nature 439, 462-465. (2006)
Стекло Леви. Относительный пропущенный свет – y, толщина образца – x.
Слайд 9 8. Случайные блуждания (случай отсутствия моментов закона прыжка
выше второго)
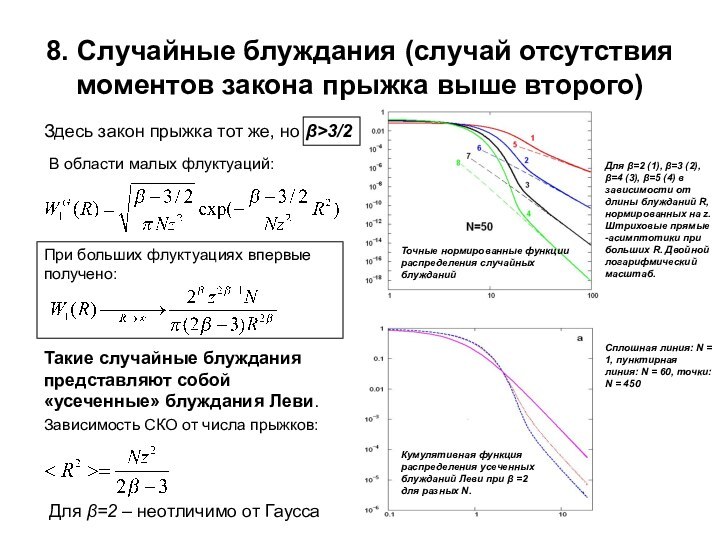
В области малых флуктуаций:
При больших флуктуациях впервые получено:
Зависимость
СКО от числа прыжков:Здесь закон прыжка тот же, но β>3/2
Для β=2 – неотличимо от Гаусса
Для =2 (1), =3 (2), =4 (3), =5 (4) в зависимости от длины блужданий R, нормированных на z. Штриховые прямые -асимптотики при больших R. Двойной логарифмический масштаб.
Кумулятивная функция распределения усеченных блужданий Леви при β =2 для разных N.
Точные нормированные функции распределения случайных блужданий
Сплошная линия: N = 1, пунктирная линия: N = 60, точки: N = 450
Такие случайные блуждания представляют собой «усеченные» блуждания Леви.
Слайд 10
9. Промежуточные выводы
Введение закона прыжка вида:
позволяет единым аналитическим
образом рассмотреть как обычные блуждания Леви, так и усеченные
блуждания Леви.Для усеченных блужданий получены аналитические асимптоты, как для области малых флуктуаций, так и для области больших флуктуаций.
Слайд 11
10. Эмпирически наблюдаемые негауссовы случайные блуждания
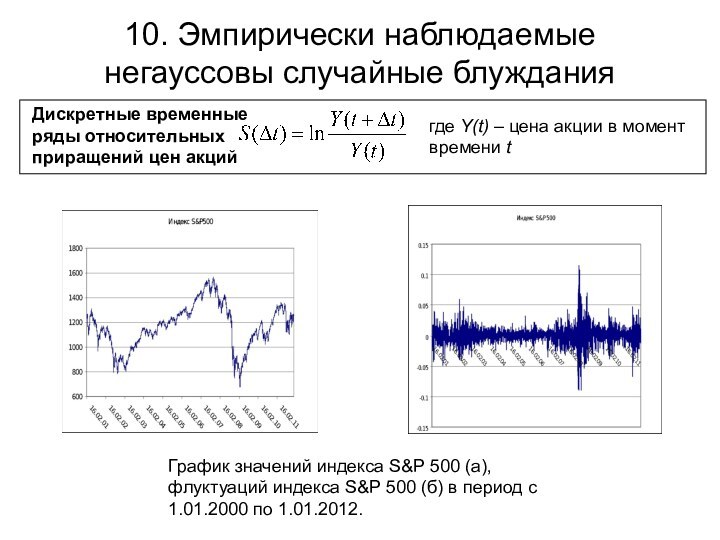
Дискретные временные ряды
относительных приращений цен акций
где Y(t) – цена акции в
момент времени tГрафик значений индекса S&P 500 (а), флуктуаций индекса S&P 500 (б) в период с 1.01.2000 по 1.01.2012.
Слайд 12
11. Статистические характеристики финансовых временных рядов
Дискретные временные ряды
относительных приращений цен акций
где Y(t) – цена акции в
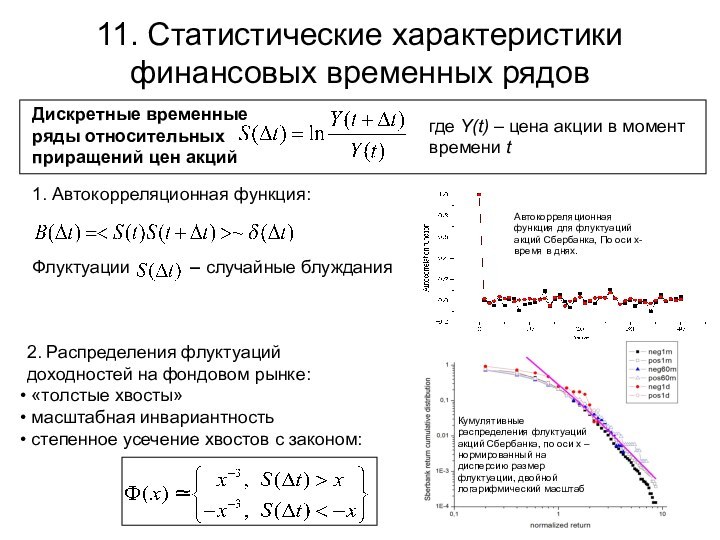
момент времени t1. Автокорреляционная функция:
Флуктуации – случайные блуждания
2. Распределения флуктуаций доходностей на фондовом рынке:
«толстые хвосты»
масштабная инвариантность
степенное усечение хвостов с законом:
Кумулятивные распределения флуктуаций акций Сбербанка, по оси x – нормированный на дисперсию размер флуктуации, двойной логарифмический масштаб
Автокорреляционная функция для флуктуаций акций Сбербанка, По оси x- время в днях.
Слайд 13
12. Определение минимального масштаба процесса
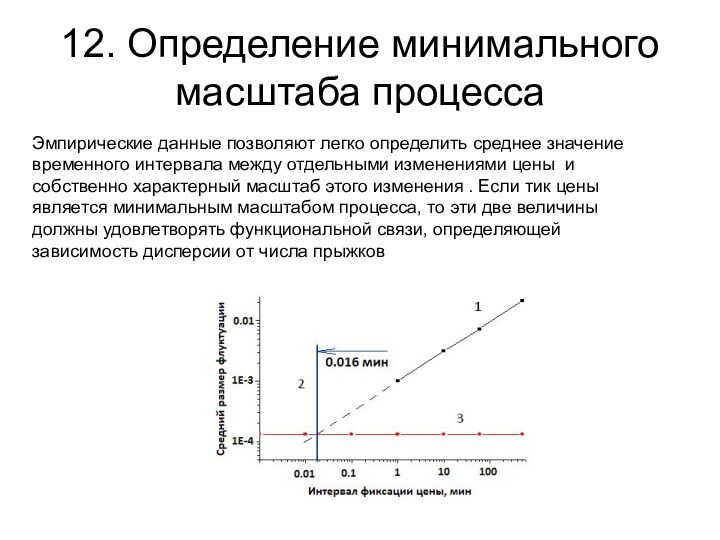
Эмпирические данные позволяют легко
определить среднее значение временного интервала между отдельными изменениями цены
и собственно характерный масштаб этого изменения . Если тик цены является минимальным масштабом процесса, то эти две величины должны удовлетворять функциональной связи, определяющей зависимость дисперсии от числа прыжковСлайд 14 13. Применение модели «усеченных» блужданий Леви для описания
рассматриваемой системы
Характер асимптотики «усеченных» блужданий Леви с законом
единичного прыжка при β=2 соответствует эмпирическим распределениям, однако в этом случае имеет место различное поведение распределения для разных значений N, чего не видно в реальности.
Попробуем применить схему случайных блужданий с непрерывным временем (CTRW). Данная модель позволяет простым образом перейти от дискретных случайных блужданий к непрерывным. Если ввести функцию плотности распределения прыжков за определенное время p(N,t), то наблюдаемая плотность распределения W(R,t) выражается формулой подчинения:
Функция распределения временных интервалов спадает с уменьшением Δt как (Δt)4.4. Учет времени между прыжками не позволяет получить новые результаты в силу наличия математического ожидания величины временного интервала.
Слайд 15
14. Модификация модели
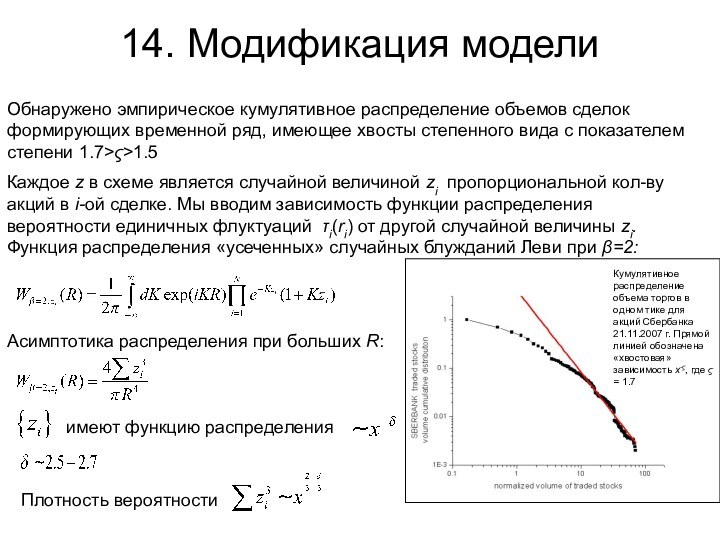
Обнаружено эмпирическое кумулятивное распределение объемов сделок
формирующих временной ряд, имеющее хвосты степенного вида с показателем
степени 1.7>ς>1.5Каждое z в схеме является случайной величиной zi пропорциональной кол-ву акций в i-ой сделке. Мы вводим зависимость функции распределения вероятности единичных флуктуаций τi(ri) от другой случайной величины zi. Функция распределения «усеченных» случайных блужданий Леви при β=2:
Асимптотика распределения при больших R:
имеют функцию распределения
Плотность вероятности
Кумулятивное распределение объема торгов в одном тике для акций Сбербанка 21.11.2007 г. Прямой линией обозначена «хвостовая» зависимость x-ς, где ς = 1.7
Слайд 16
15. Сравнение результатов модели и эмпирических данных.
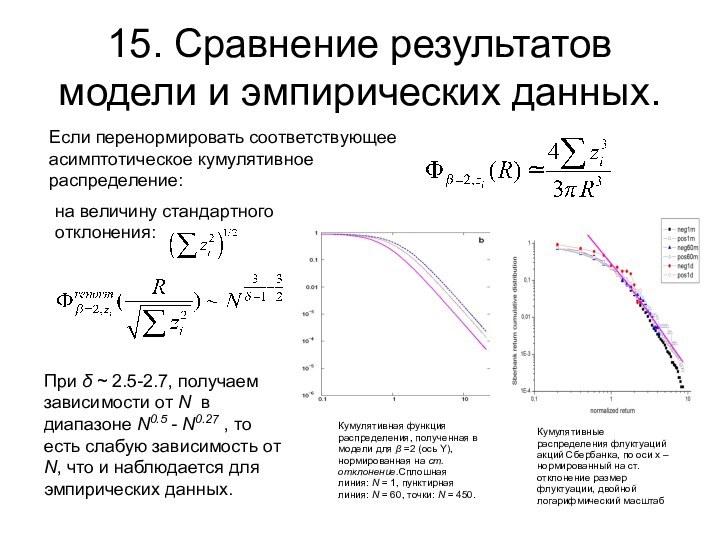
Если перенормировать
соответствующее асимптотическое кумулятивное распределение:
на величину стандартного отклонения:
При δ
~ 2.5-2.7, получаем зависимости от N в диапазоне N0.5 - N0.27 , то есть слабую зависимость от N, что и наблюдается для эмпирических данных. Кумулятивные распределения флуктуаций акций Сбербанка, по оси x – нормированный на ст. отклонение размер флуктуации, двойной логарифмический масштаб
Кумулятивная функция распределения, полученная в модели для β =2 (ось Y), нормированная на ст. отклонение.Сплошная линия: N = 1, пунктирная линия: N = 60, точки: N = 450.
Слайд 17
16. Выводы
Введение закона прыжка позволяет единым аналитическим
образом рассмотреть как обычные блуждания Леви, так и «усеченные»
блуждания Леви.Для усеченных блужданий получены аналитические асимптоты и выяснены законы масштабирования.
Исследована система, в которой наблюдаются негауссовы случайные блуждания, представляющая собой динамику цен акций на российском фондовом рынке.
Кумулятивные распределения флуктуаций российских акций и индексов обладают скейлингом, а асимптотика при больших флуктуациях описывается законом типа 1/x3.
Установлен закон прыжка, удовлетворяющий исследованной системе
Предложена схема модификации модели, позволяющая получить точный аналитический вид распределения, хорошо описывающий реальные данные.
Слайд 18
Публикации
1. Видов П.В., Романовский М.Ю., Доходность активов российского
фондового рынка: автокорреляции и распределения, "Математика. Компьютер. Образование", Тезисы
XV международной конференции (2008)2. Видов П.В., Жуков И.А., Романовский М.Ю., Доходность активов российского фондового рынка: автокорреляции и распределения, "Математика. Компьютер. Образование". Cб. трудов XV международной конференции, Ижевск: Научно-издательский центр "Регулярная и хаотическая динамика", (2008). Том 1, 302 стр. Стр. 196-201
3. П.В. Видов, М.Ю. Романовский, Аналитические представления негауссовых законов случайных блужданий, Труды Института общей физики им. А.М. Прохорова, Т.65, (2009)
4. P.V.Vidov and M.Yu.Romanovsky. Analytical representation of non-Gaussian laws of random walks, Physics of wave phenomena. (2009). V.17, No.3. P.218-228.
5. М.Ю.Романовский, П.В. Видов, В.А. Пыркин, Является ли тик элементарным прыжком в схеме случайных блужданий на фондовом рынке? Компьютерные исследования и моделирование, Т.2, № 2, с.219-223, (2010)
6. Видов П.В., Романовский М.Ю., "Неклассические случайные блуждания и феноменология флуктуаций доходности ценных бумаг на фондовом рынке" УФН, 181, 774–778 (2011)
7. M.Yu. Romanovsky, P.V. Vidov, Analytical representation of stock and stock-indexes returns: Non-Gaussian random walks with various jump laws, Physica A, 390, 21-22 (2011)