Слайд 2
1. Инертность тел. Масса. Импульс. Сила.
Раздел механики,
изучающий законы взаимодействия тел, называется динамикой.
Опыт показывает, что всякое
тело «оказывает сопротивление» при любых попытках изменить его скорость, как по модулю, так и по направлению. Это свойство, выражающее степень сопротивления тела к изменению его скорости, называют инертностью.
Масса – это свойство тела, характеризующее его инертность.
В системе СИ масса измеряется в килограммах (кг).
Один килограмм – это масса эталона, хранящегося в Палате мер и весов в Севре (Франция), одна двенадцатая от суммарной массы 6,022·1026 атомов изотопа углерода‑12 или масса 1·10‑3 м3 воды при температуре +40о C.
Слайд 3
Произведение массы тела на его скорость именуется импульсом
тела: .
В системе
СИ импульс измеряется в кг·м/с.
Сказанное про массу и изменение скорости верно не во всех системах, а только в тех, где при отсутствии внешних воздействий скорость движения тел не меняется. Такие системы отсчета, в которых не меняются вектора скорости всех тел, которые не испытывают внешних воздействий (или внешние воздействия скомпенсированы) называются инерциальными. Понятие инерции введено Галилео Галилеем в 1632 году.
Сила – это количественная мера взаимодействия тел.
Сила является причиной изменения скорости тела. В механике Ньютона силы могут иметь различную физическую причину: сила трения, сила тяжести, упругая сила и т. д.
Сила является векторной величиной. Векторная сумма всех сил, действующих на тело, называется равнодействующей силой.
В системе СИ сила измеряется в Ньютонах: 1 Н = (кг·м)/с2
Слайд 4
2. Законы Ньютона
Первый Закон Ньютона
Законы динамики были
открыты великим ученым И. Ньютоном (1687 г.). Три закона динамики,
сформулированные Ньютоном, лежат в основе так называемой классической механики. Законы Ньютона следует рассматривать как обобщение опытных фактов.
Первый закон Ньютона: существуют системы отсчета, называемые инерциальными, в которых при отсутствии воздействия других тел частица сохраняет стационарное состояние движения: движется равномерно и прямолинейно (в частном случае - покоится).
Другая формулировка первого закона Ньютона: существуют инерциальные системы отсчёта.
Слайд 5
Второй закон Ньютона
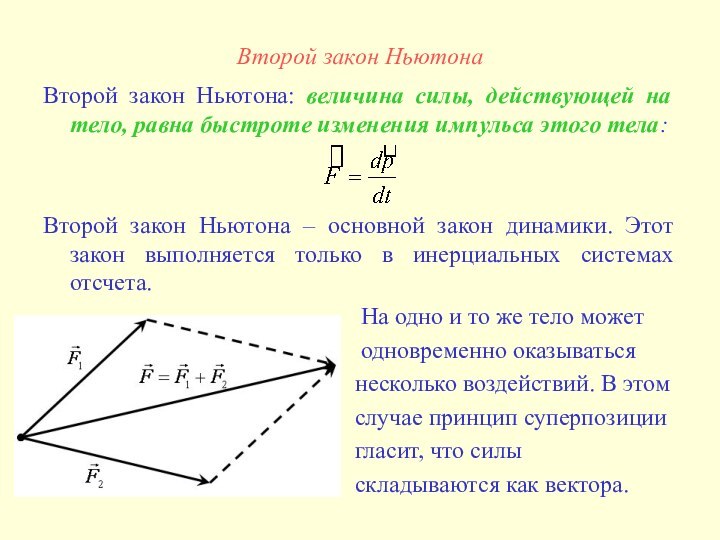
Второй закон Ньютона: величина силы,
действующей на тело, равна быстроте изменения импульса этого тела:
Второй закон Ньютона – основной закон динамики. Этот закон выполняется только в инерциальных системах отсчета.
На одно и то же тело может
одновременно оказываться
несколько воздействий. В этом
случае принцип суперпозиции
гласит, что силы
складываются как вектора.
Слайд 6
Третий закон Ньютона
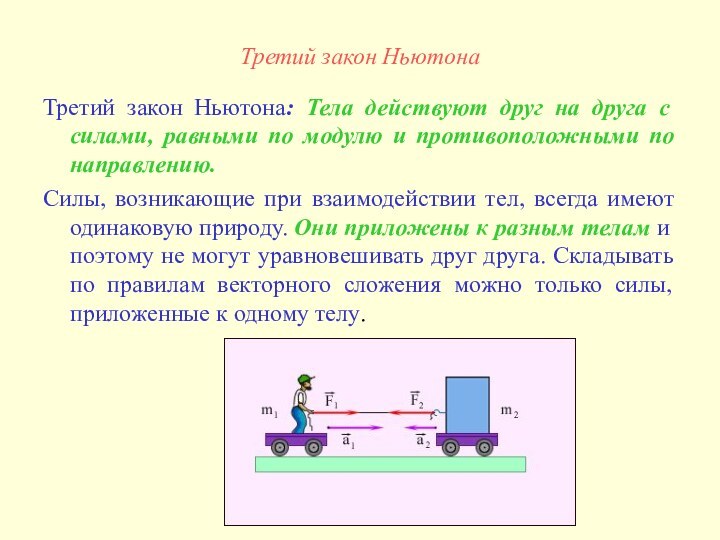
Третий закон Ньютона: Тела действуют
друг на друга с силами, равными по модулю и
противоположными по направлению.
Силы, возникающие при взаимодействии тел, всегда имеют одинаковую природу. Они приложены к разным телам и поэтому не могут уравновешивать друг друга. Складывать по правилам векторного сложения можно только силы, приложенные к одному телу.
Слайд 7
3. Виды сил в механике
3.1. Сила тяготения
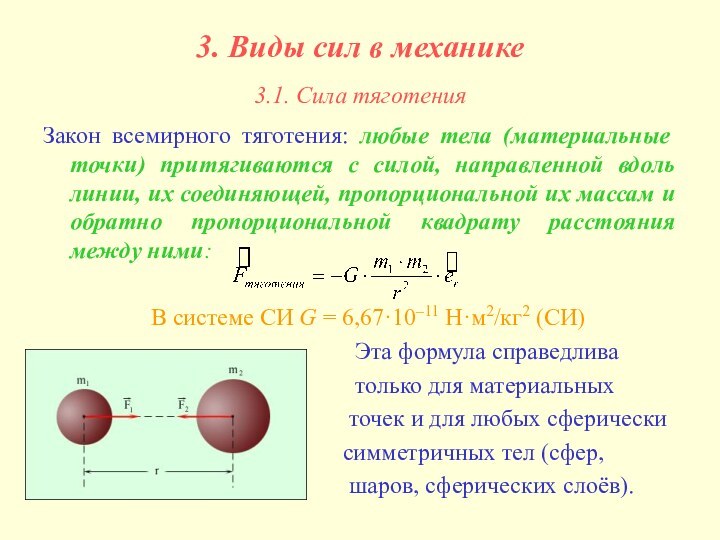
Закон
всемирного тяготения: любые тела (материальные точки) притягиваются с силой,
направленной вдоль линии, их соединяющей, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:
В системе СИ G = 6,67·10–11 Н·м2/кг2 (СИ)
Эта формула справедлива
только для материальных
точек и для любых сферически
симметричных тел (сфер,
шаров, сферических слоёв).
Слайд 8
Сила тяжести
Если ввести переменную g, то закон
всемирного тяготения
будет выглядеть так:
,
Заметим, что масса как мера инерции, входящая в уравнение для второго закона Ньютона, в точности равна массе как мере гравитации, входящей в закон всемирного тяготения. Это утверждение носит название принципа эквивалентности инертной и гравитационной масс и подтверждено с высокой точностью многочисленными экспериментами.
В тех задачах, где изменение расстояния между центрами гравитационно взаимодействующих тел намного меньше самого расстояния, величину изменения обычно можно считать несущественной и принимать постоянной для всех точек пространства, описываемых в задаче.
Слайд 9
3.2. Реакция опоры и натяжение нити
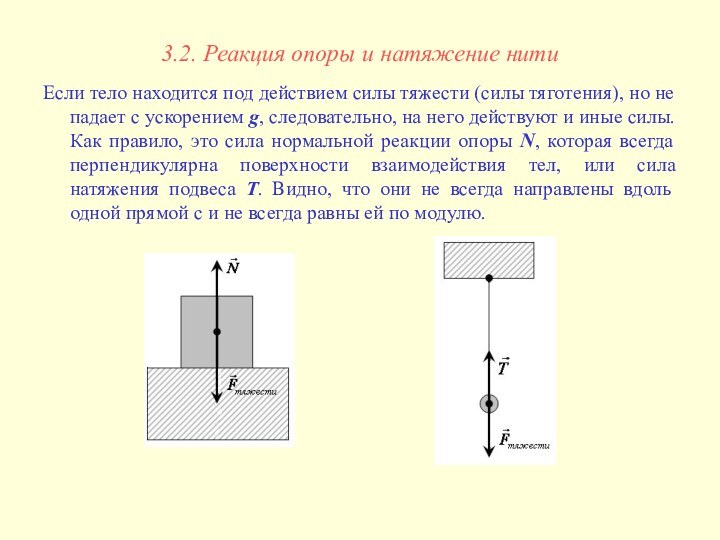
Если тело
находится под действием силы тяжести (силы тяготения), но не
падает с ускорением g, следовательно, на него действуют и иные силы. Как правило, это сила нормальной реакции опоры N, которая всегда перпендикулярна поверхности взаимодействия тел, или сила натяжения подвеса Т. Видно, что они не всегда направлены вдоль одной прямой с и не всегда равны ей по модулю.
Слайд 10
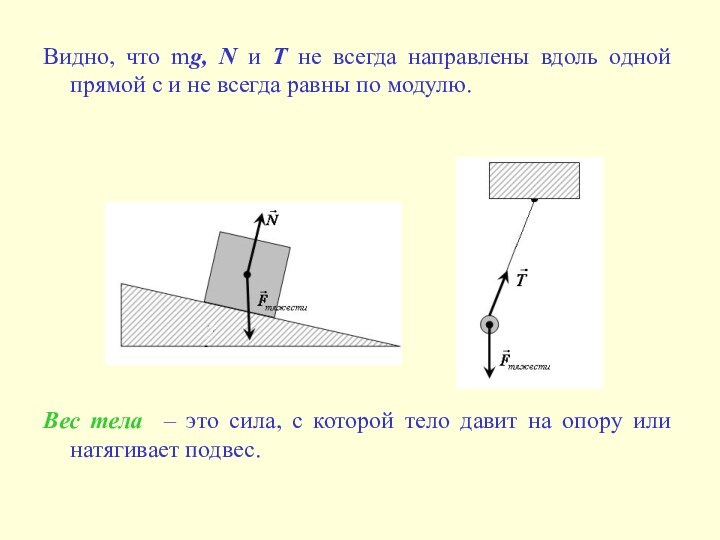
Видно, что mg, N и T не всегда
направлены вдоль одной прямой с и не всегда равны
по модулю.
Вес тела – это сила, с которой тело давит на опору или натягивает подвес.
Слайд 11
3.3. Сила трения
Трение – один из видов
взаимодействия тел. Оно возникает при соприкосновении двух тел. Трение,
как и все другие виды взаимодействия, подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело. Силы трения, как и упругие силы, имеют электромагнитную природу. Они возникают вследствие взаимодействия между атомами и молекулами соприкасающихся тел.
Выделяют два типа сил трения: сухого и вязкого.
Слайд 12
Сухое трение
Различают силы трения покоя, скольжения и качения.
Сила
трения покоя возникают, когда вдоль границы раздела двух тел,
неподвижных друг относительно друга. При этом и скорость, и ускорение равны нулю, поэтому
,
где – все прочие силы. Когда сила сухого трения скольжения достигает максимально возможной (предельной) величины, то тела начинают двигаться друг относительно друга. Эта предельная величина рассчитывается по формуле
,
где – коэффициент трения покоя, зависящий только от природы контактирующих веществ, качества поверхностей и от температуры.
Слайд 13
Сила сухого трения скольжения
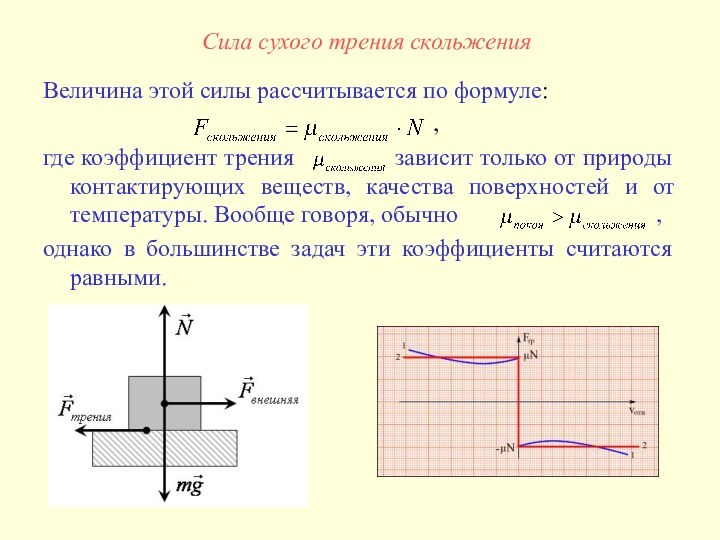
Величина этой силы рассчитывается
по формуле:
,
где коэффициент трения зависит только от природы контактирующих веществ, качества поверхностей и от температуры. Вообще говоря, обычно ,
однако в большинстве задач эти коэффициенты считаются равными.
Слайд 14
Сила трения качения
Перемещению катящегося тела мешает образование
углубления под ним и «горки» перед ним. Величина силы
трения качения рассчитывается по формуле: ,
где коэффициент трения зависит только от природы контактирующих веществ, качества поверхностей и от температуры. Обычно .
Слайд 15
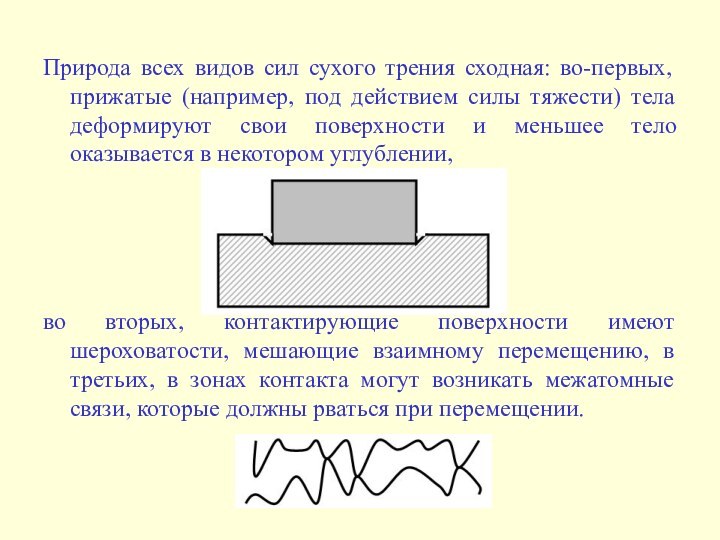
Природа всех видов сил сухого трения сходная: во-первых,
прижатые (например, под действием силы тяжести) тела деформируют свои
поверхности и меньшее тело оказывается в некотором углублении,
во вторых, контактирующие поверхности имеют шероховатости, мешающие взаимному перемещению, в третьих, в зонах контакта могут возникать межатомные связи, которые должны рваться при перемещении.
Слайд 16
Вязкое трение
При движении твердого тела в жидкости или
газе возникает силa вязкого трения. Сила вязкого трения значительно
меньше силы сухого трения. Она также направлена в сторону, противоположную относительной скорости тела. При вязком трении нет трения покоя.
Сила вязкого трения сильно зависит от скорости тела. При достаточно малых скоростях Fтр ~ υ, при больших скоростях Fтр ~ υ2. При этом коэффициенты пропорциональности в этих соотношениях зависят от формы тела.
Слайд 17
3.4. Сила упругости и деформация твердых тел
При
деформации тела возникает сила, которая стремится восстановить прежние размеры
и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
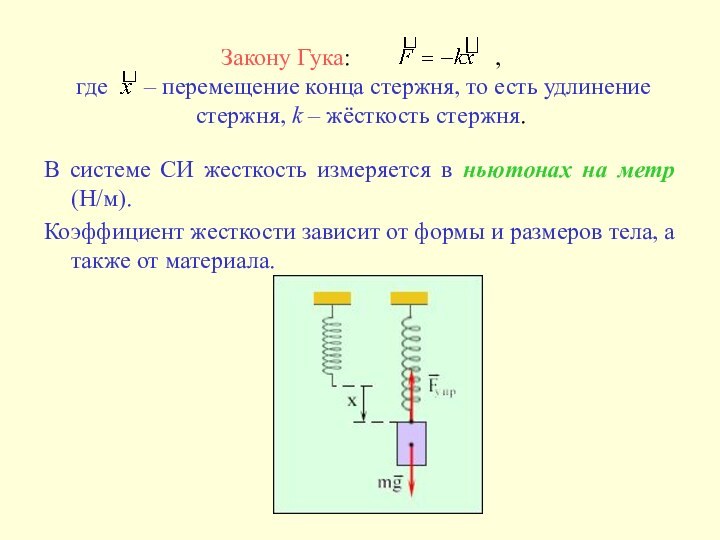
,
где
– перемещение конца стержня, то есть удлинение стержня, k – жёсткость стержня.
В системе СИ жесткость измеряется в ньютонах на метр (Н/м).
Коэффициент жесткости зависит от формы и размеров тела, а также от материала.
Слайд 19
В физике закон Гука для деформации растяжения или
сжатия принято записывать в другой форме.
Отношение ε = x/l называется
относительной деформацией,
а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением.
Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела.
Для различных материалов модуль Юнга меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.
Слайд 20
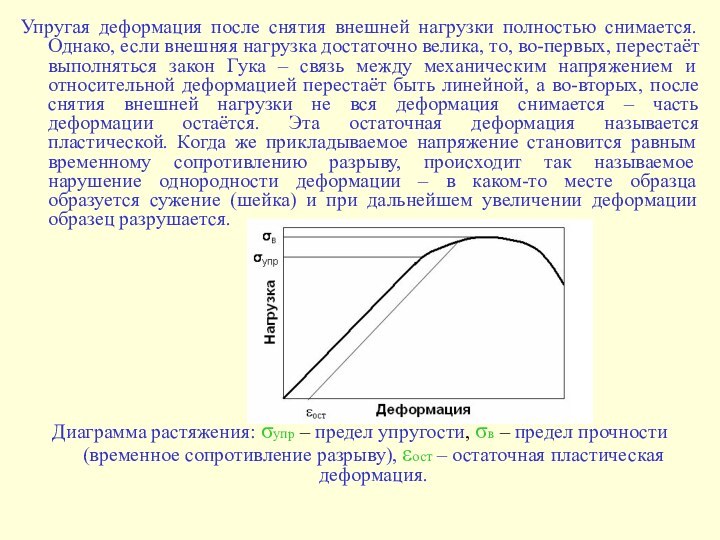
Упругая деформация после снятия внешней нагрузки полностью снимается.
Однако, если внешняя нагрузка достаточно велика, то, во-первых, перестаёт
выполняться закон Гука – связь между механическим напряжением и относительной деформацией перестаёт быть линейной, а во-вторых, после снятия внешней нагрузки не вся деформация снимается – часть деформации остаётся. Эта остаточная деформация называется пластической. Когда же прикладываемое напряжение становится равным временному сопротивлению разрыву, происходит так называемое нарушение однородности деформации – в каком-то месте образца образуется сужение (шейка) и при дальнейшем увеличении деформации образец разрушается.
Диаграмма растяжения: σупр – предел упругости, σв – предел прочности (временное сопротивление разрыву), εост – остаточная пластическая деформация.
Слайд 21
4. Инерциальные и неинерциальные системы отсчета
Слайд 22
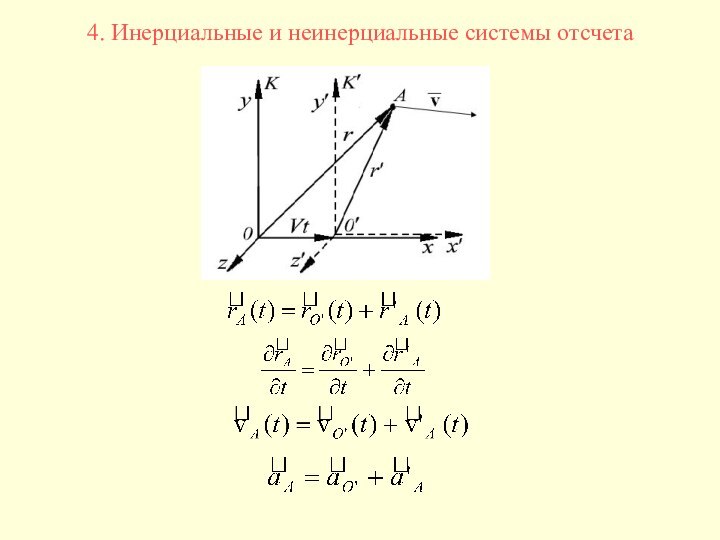
Если у нас обе системы инерциальные (то есть
) и тело A
движется с ускорением , то – ускорение инвариантно по отношению к переходу из одной инерциальной системы отсчёта в другую.
Ускорения появляются при наличии силы, действующей на тело A: .
То есть, при переходе из одной инерциальной системы отсчёта в другую силы, действующие на тела, не меняются. А следовательно, выполняется принцип относительности Галилея: все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли данная система отсчёта или движется равномерно и прямолинейно. Поскольку
, то – преобразование Галилея.