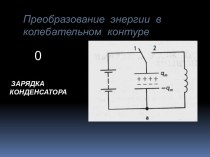
Слайд 2
Тепловое равновесие.
Температура.
Молекулярная физика и термодинамика изучают свойства
и поведение макроскопических систем, т.е. систем, состоящих из огромного
числа атомов и молекул. Типичные системы, с которыми мы сталкиваемся в повседневной жизни, содержат около 1025 атомов.
Состояние макроскопической системы, в котором она может находиться неопределённо долгое время, называется равновесным .
Равновесное состояние системы в целом может быть описано при помощи величин, называемых макроскопическими параметрами, к числу которых относят давление, объем и т. д. Каждый из параметров характеризует некоторое свойство системы. Так объем V мера свойства системы занимать ту или иную область пространства; давление Р – мера свойства системы сопротивляться внешнему изменению ее объёма.
Слайд 3
Одним из наиболее важных параметров, характеризующих равновесные свойства
макроскопической системы, является температура.
Введем этот параметр, для
чего рассмотрим два тела, которые могут взаимодействовать и обмениваться энергией. Этот тип взаимодействия, который называется тепловым, приводит к тому, что в результате столкновений молекул в области контакта двух тел происходит передача энергии от быстрых молекул к медленным. Это означает, что энергия движения атомов в одном теле уменьшается, в другом – увеличивается. Тело, которое теряет энергию, называют более нагретым, а тело, к которому энергия переходит – менее нагретым. Такой переход энергии продолжается до тех пор, пока не установится состояние теплового равновесия. В состоянии теплового равновесия степени нагретости тел одинаковы. Для характеристики степени нагретости тела вводят параметр, называемый температурой.
Слайд 4
Теория создана немецким физиком Р. Клаузисом в 1957
году для модели реального газа, которая называется идеальный газ.
Основные признаки модели:
расстояния между молекулами велики по сравнению с их размерами;
взаимодействие между молекулами на расстоянии отсутствует;
при столкновениях молекул действуют большие силы отталкивания;
время столкновения много меньше времени свободного движения между столкновениями.
Идеальный газ. Основное уравнение молекулярно-кинетической теории идеального газа.
Слайд 5
Молекулярно-кинетическая теория (МКТ) устанавливает связи между макро- и
микропараметрами идеального газа. Основное уравнение МКТ выражает связь давления
газа со средней кинетической энергией поступательного движения молекул. Давление газа на стенки сосуда является результатом многочисленных ударов молекул. При каждом ударе стенка получает силовой импульс, величина которого зависит от скорости молекул и, следовательно, от энергии их движения. При огромном числе ударов создается постоянное давление газа на стенку. Число ударов зависит от концентрации молекул n. Таким образом, можно ожидать, что давление газа связано с концентрацией молекул и с энергией их движения. Получим основное уравнение МКТ.
Слайд 6
Средняя квадратичная скорость молекул.
Из основного уравнения молекулярно-кинетической теории
можно получить формулу для расчета средней квадратичной скорости молекул.
Произведение
массы одной молекулы m0 на число молекул в единице объема n равно плотности вещества m0n.
Слайд 7
Экспериментальные газовые законы
Всякое изменение состояния газа называется
термодинамическим процессом.
Простейшими процессами в идеальном газе являются изопроцессы. Это
процессы, при которых масса газа и один из его параметров состояния (температура, давление или объем) остаются постоянными.
Изопроцесс, протекающий при постоянной температуре, называется изотермическим.
Экспериментально Р. Бойлем и Э. Мариоттом было установлено, что при постоянной температуре произведение давления газа на объем для данной массы газа есть величина постоянная (закон Бойля–Мариотта):
Графически этот закон в координатах РV изображается линией, называемой изотермой.
Слайд 8
Изопроцесс, протекающий в идеальном газе, в ходе которого
давление остается постоянным, называется изобарным.
Зависимость объема газа от его
температуры при постоянном давлении была установлена Л. Гей-Люссаком, который показал, что объем газа данной массы при постоянном давлении возрастает линейно c увеличением температуры (закон Гей-Люссака):
V = V0·(1 + a·t), где V – объем газа при температуре t, °С; V0 – его объем при 0°С.
Величина называется температурным коэффициентом объемного расширения. Для всех газов a = (1/273°С–1). Следовательно,
V = V0·(1 + ·t).
Графически зависимость объема от температуры изображается прямой линией – изобарой
Слайд 9
Изопроцесс, протекающий в газе, при котором объем остается
постоянным, называется изохорным.
Исследования зависимости давления данной массы газа от
температуры при неизменном объеме были впервые проведены французским физиком Шарлем. Им было установлено, что давление газа данной массы при постоянном объеме возрастает линейно с увеличением температуры (закон Шарля):
P = P0(1+ t).
Величина называется температурным коэффициентом давления. Ее значение не зависит от природы газа; для всех газов = 1/273 °С–1.
Слайд 10
Абсолютная шкала температур.
Если изохору продолжить в область
отрицательных температур, то в точке пересечения с осью абсцисс
имеем
P = P0(1 + ·t) = 0
Отсюда температура, при которой давление идеального газа обращается в нуль, t = –273°С (точнее,–273,16°С). Эта температура выбрана в качестве начала отсчета термодинамической шкалы температур, которая была предложена английским ученым Кельвиным. Эта температура называется нулем Кельвина (или абсолютным нулем).
Слайд 11
Уравнение Клапейрона или объединённый газовый закон
Уравнение состояния идеального
газа – уравнение Менделеева-Клапейрона