по скоростям
Закон Максвелла описывает функцию
f(v), которая называется функцией распределения молекул по скоростям. Функция распределения молекул идеального газа по скоростям:
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


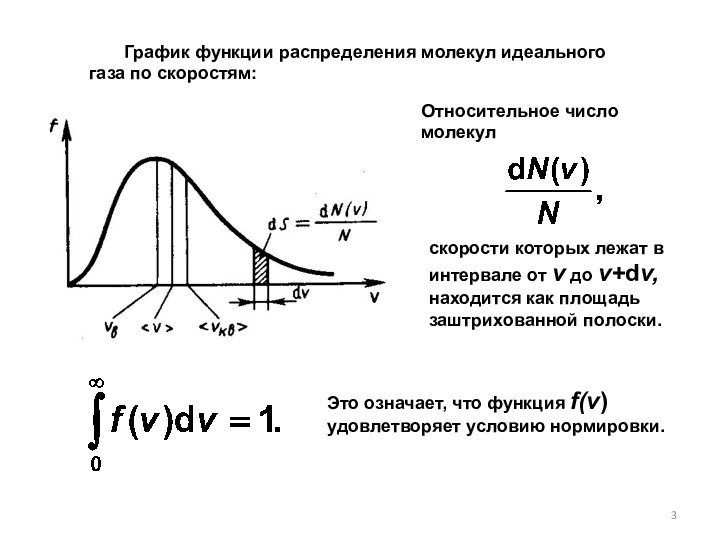


































Функция распределения молекул идеального газа по скоростям:
Это означает, что функция f(v) удовлетворяет условию нормировки.
Относительное число молекул
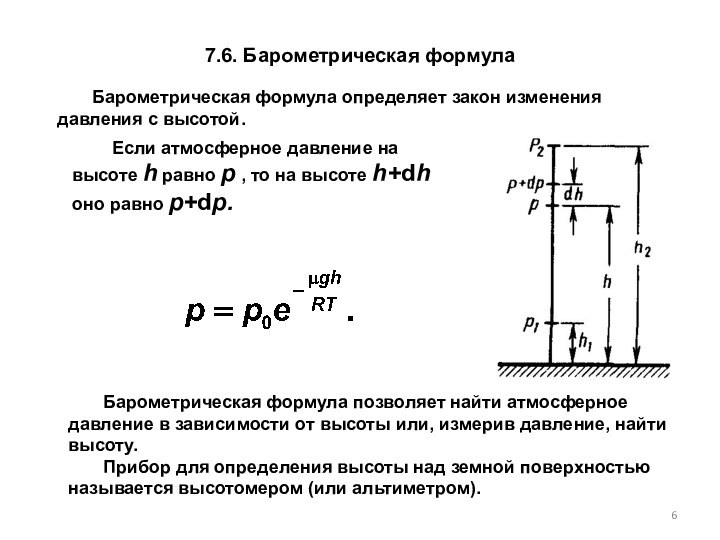
Барометрическая формула определяет закон изменения давления с высотой.
Если атмосферное давление на высоте h равно р , то на высоте h+dh оно равно p+dp.
Обозначим: П=m0gh — потенциальная энергия молекулы, то:
Поскольку p=n k T, то барометрическую формулу можно записать в виде:
Заменим:
– формула распределения Больцмана.
Под длиной пробега понимают среднюю длину свободного пробега молекул Если Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d:
Средняя длина свободного пробега молекул:
Броуновское движение взвешенных частиц вызывается ударами молекул среды, в которой частицы взвешены.
Броуновское движение — беспорядочное движение микроскопических видимых, взвешенных в жидкости или газе частиц твердого вещества, вызываемое тепловым движением частиц жидкости или газа.
При нагревании серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю поверхность второго цилиндра, давая изображение щели О.
Исследуя толщину осажденного слоя, можно оценить распределение молекул по скоростям, которое соответствует максвелловскому распределению.
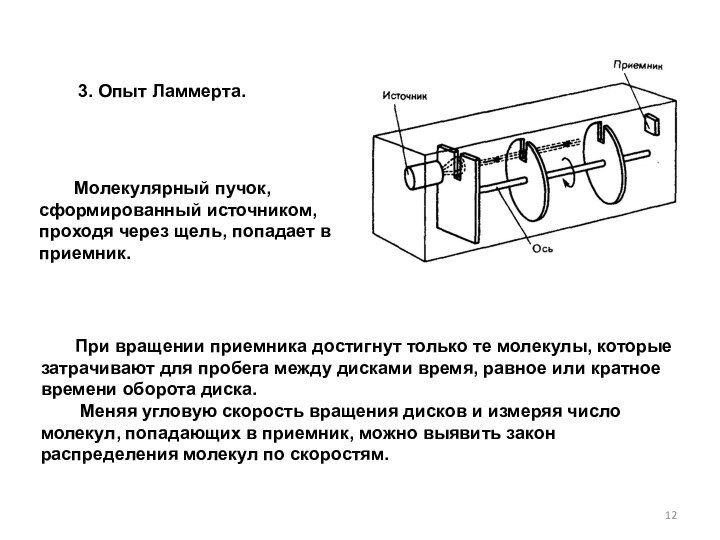
При вращении приемника достигнут только те молекулы, которые затрачивают для пробега между дисками время, равное или кратное времени оборота диска.
Меняя угловую скорость вращения дисков и измеряя число молекул, попадающих в приемник, можно выявить закон распределения молекул по скоростям.
Перенос энергии в форме теплоты подчиняется закону Фурье:
jE — плотность теплового потока, величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х,
λ — теплопроводность,
— градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке.
— плотность газа,
— средняя скорость теплового движения молекул,
— средняя длина свободного пробега.
Явление диффузии для химически однородного газа подчиняется закону Фука:
jm — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х,
D — диффузия (коэффициент диффузии),
dρ/dx — градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке.
Взаимодействие двух слоев согласно второму закону Ньютона можно рассматривать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе.
jp — плотность потока импульса — величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х,
Из записанных выше формул вытекают простые зависимости между λ, D и η :
8.1. Внутренняя энергия и число степеней свободы
Термодина́мика — раздел физики, изучающий соотношения и превращения теплоты и других форм энергии.
Любая термодинамическая система обладает определенной внутренней энергией.
Внутренняя энергия — энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц.
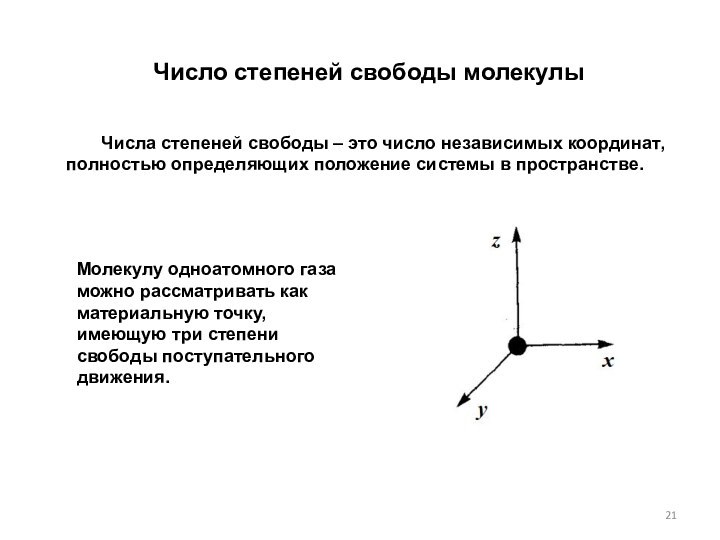
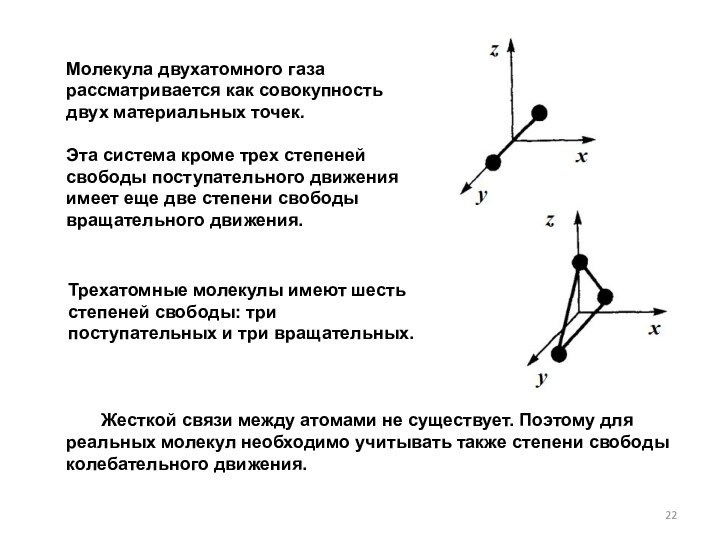
Молекулу одноатомного газа можно рассматривать как материальную точку, имеющую три степени свободы поступательного движения.
Трехатомные молекулы имеют шесть степеней свободы: три поступательных и три вращательных.
Жесткой связи между атомами не существует. Поэтому для реальных молекул необходимо учитывать также степени свободы колебательного движения.
На каждую поступательную и вращательную степени свободы приходится кинетическая энергия:
На каждую колебательную степень свободы энергия:
Внутренняя энергия для произвольной массы т газа:
М — молярная масса, ν — количество вещества.
Существует две формы изменения внутренней энергии системы: передача теплоты и работа против внешних.
Q - количество теплоты, полученным системой,
А - работа, совершаемая системой против внешних сил.
Первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение работы против внешних сил.
Т. е., если система вернулась в исходное состояние, то изменение внутренней энергии равно нулю, а работа при этом нулю не равна:
Другая формулировка первого начала термодинамики
тогда, согласно первому началу термодинамики:
Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии равно нулю:
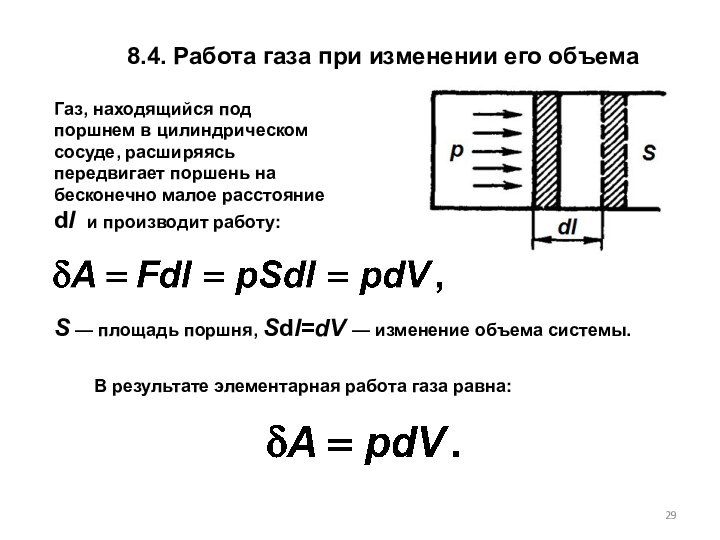
S — площадь поршня, Sdl=dV — изменение объема системы.
В результате элементарная работа газа равна:
Молярная теплоемкость—величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:
[Дж/(кг ⋅ К)]
— количество вещества.
[Дж/(моль ⋅ К]
Удельная теплоемкость с связана с молярной Сm, соотношением:
М — молярная масса вещества.
Молярная теплоемкость газа при постоянном объеме СV равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1 К.
Если:
то:
Оно показывает, что Ср всегда больше СV на величину молярной газовой постоянной.
При рассмотрении термодинамических процессов важную роль играет отношение Сp к СV :
— коэффициент Пуассона.
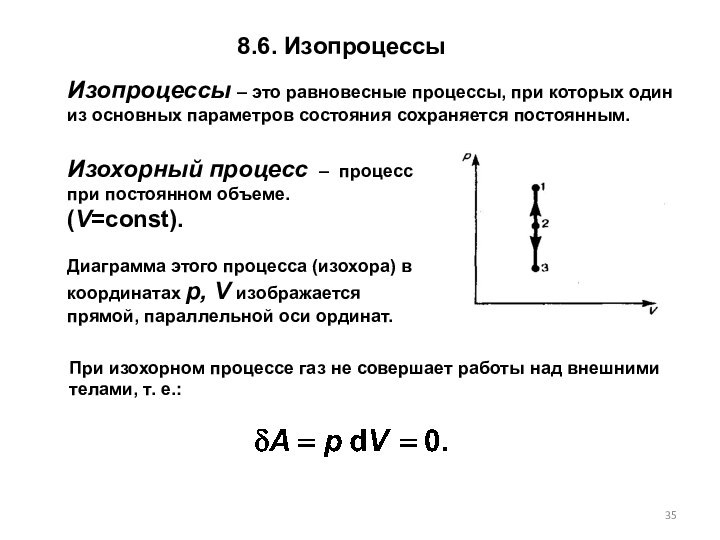
При изохорном процессе газ не совершает работы над внешними телами, т. е.:
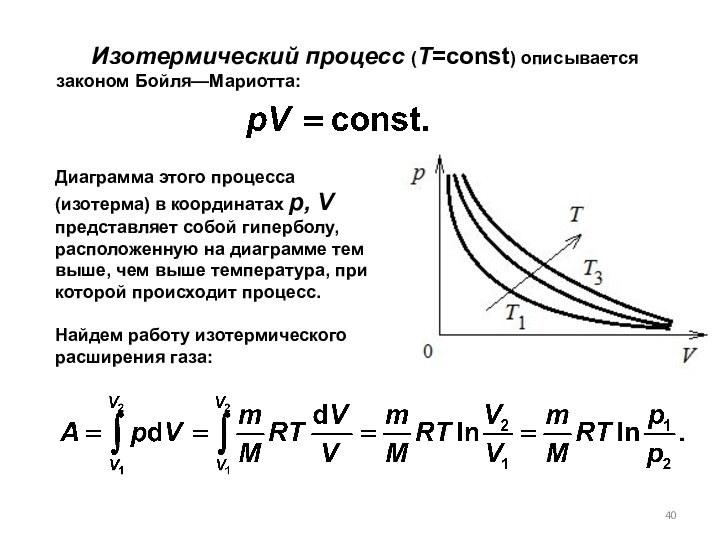
8.6. Изопроцессы
Поскольку
то для произвольной массы газа получим:
Из первого начала термодинамики:
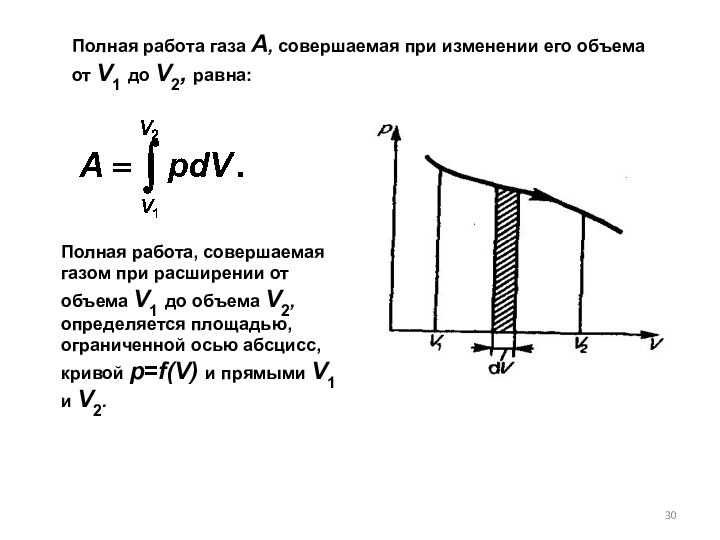
(определяется площадью заштрихованного прямоугольника).
При изобарном процессе работа газа при увеличения объема от V1 до V2 равна:
его внутренняя энергия возрастает на величину:
В изобарном процессе при сообщении газу массой т количества теплоты:
т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
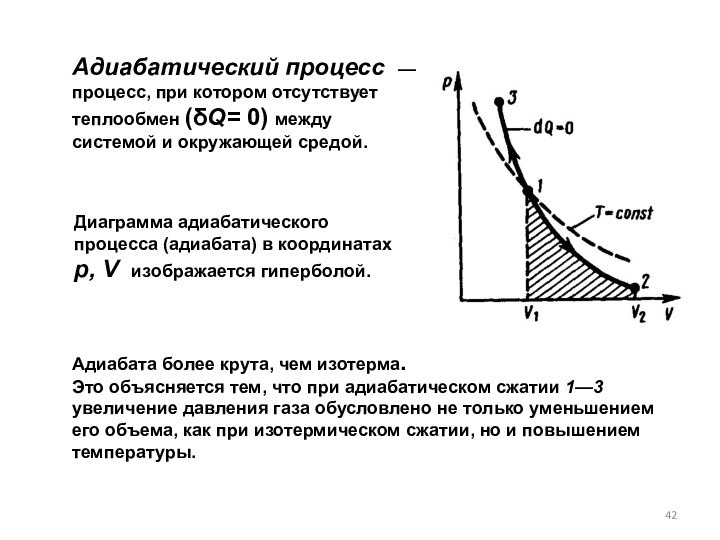
Адиабата более крута, чем изотерма.
Это объясняется тем, что при адиабатическом сжатии 1—3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.
тогда:
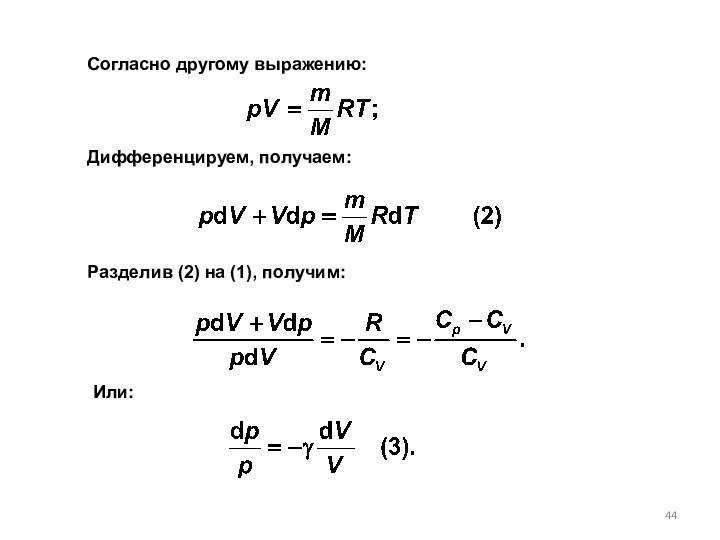
8.7. Уравнение адиабатического процесса (уравнение Пуассона)
получим другие выражения адиабатического процесса:
Исходя из первого начала термодинамики при условии постоянства теплоемкости (C=const) можно вывести уравнение политропы:
n=(С—Сp)/(С—СV)—показатель политропы.