Слайд 2
Большинство задач теоретической и математической физики приводят к
нелинейным уравнением. Именно нелинейные системы поражают разнообразием и неисчерпаемым
запасом уникальных эффектов, которые находят многочисленные приложения в науке и технике. Наиболее актуальные проблемы требуют немедленного анализа, хотя в настоящее время нет общих методов решения систем нелинейных уравнений
Слайд 3
ТУРБУЛЕНТНОСТЬ
Турбулентность — слово далеко не новое. Вам оно известно
как слово, описывающее внезапную тряску во время полета. Тем
не менее турбулентность в механике жидкостей — совершенно другое дело. Летная турбулентность, технически называемая «турбулентностью при ясном небе», возникает при встрече двух воздушных тел, движущихся на разных скоростях. Физики, однако, с трудом объясняют это явление турбулентности в жидкостях.
Слайд 4
ТУРБУЛЕНТНОСТЬ
Турбулентность в жидкостях окружает нас всюду. Струя, вытекающая
из крана, полностью распадается на хаотичные частицы жидкости, отличные
от единого потока, которые мы получаем, когда открываем кран. Это один из классических примеров турбулентности, который используется для объяснения явления школьникам и студентам.
Слайд 5
ТУРБУЛЕНТНОСТЬ
Турбулентность распространена в природе, ее можно встретить в
различных геофизических и океанических потоках. Она также важна для
инженеров, поскольку часто рождается в потоках над лопастями турбин, закрылками и другими элементами. Турбулентность характеризуется случайными колебаниями в таких переменных, как скорость и давление.
Слайд 6
ТУРБУЛЕНТНОСТЬ
Хотя на тему турбулентности было проведено много экспериментов
и получено много эмпирических данных, мы все еще далеки
от убедительной теории о том, что именно вызывает турбулентность в жидкости, как она контролируется и что именно упорядочивает этот хаос. Решение проблемы осложняется еще и тем, что уравнения, определяющие движение жидкости — уравнения Навье-Стокса — весьма трудно анализировать.
Слайд 7
ТУРБУЛЕНТНОСТЬ
Ученые прибегают к высокопроизводительным методикам вычислений, наряду с
экспериментами и теоретическими упрощениями в процессе изучения явления, но
полной теории турбулентности нет и нет.
Слайд 8
ТУРБУЛЕНТНОСТЬ
Таким образом, турбулентность жидкости остается одной из важнейших
нерешенных проблем физики на сегодняшний день. Нобелевский лауреат Ричард
Фейнман назвал ее «наиболее важной нерешенной проблемой классической физики».
Слайд 9
ТУРБУЛЕНТНОСТЬ
Когда квантового физика Вернера Гейзенберга спросили, если бы
он предстал перед Богом и получил возможность попросить его
о чем угодно, что бы это было, физик ответил: «Я задал бы ему два вопроса. Почему относительность? И почему турбулентность? Думаю, на первый вопрос у него точно будет ответ».
Слайд 10
ТУРБУЛЕНТНОСТЬ
Основная проблема в том, что интересные нам проблемы
турбулентных потоков почти всегда в высочайшей степени нелинейны, и
математики, которая сумела бы справиться с такими чрезвычайно нелинейными проблемами, похоже, не существует. Среди многих физиков долгое время было распространено поверье, что когда в их теме всплывает новая проблема, каким-то образом, словно по волшебству, необходимая для решения математика вдруг оказывается уже изобретенной.
Слайд 11
ТУРБУЛЕНТНОСТЬ
Важность изучений турбулентности породила новое поколение вычислительных методик.
Решение, хотя бы приблизительное, теории турбулентности позволит науке делать
лучшие прогнозы погоды, проектировать энергоэффективные автомобили и самолеты и лучше понимать различные природные явления.
Слайд 12
Человеку даже без специального физического или технического образования
несомненно знакомы слова "электрон, протон, нейтрон, фотон". А вот
созвучное с ними слово "солитон" многие, вероятно, слышат впервые. Это и неудивительно: хотя то, что обозначается этим словом, известно более полутора столетий, надлежащее внимание солитонам стали уделять лишь с последней трети ХХ века. Солитонные явления оказались универсальными и обнаружились в математике, гидромеханике, акустике, радиофизике, астрофизике, биологии, океанографии, оптической технике.
Слайд 13
Во всех вышеперечисленных областях есть одна общая черта:
в них или в отдельных их разделах изучаются волновые
процессы, а проще говоря - волны. В наиболее общем смысле волна - это распространение возмущения какой-либо физической величины, характеризующей вещество или поле. Это распространение обычно происходит в какой-то среде - воде, воздухе, твердых телах.
Слайд 14
Возможность существования солитонов в оптическом волокне предсказал в
1972 году физик-теоретик Акира Хасегава, сотрудник фирмы "Белл". Но
в то время еще не было световодов с низкими потерями в тех областях длин волн, где можно наблюдать солитоны.
Слайд 15
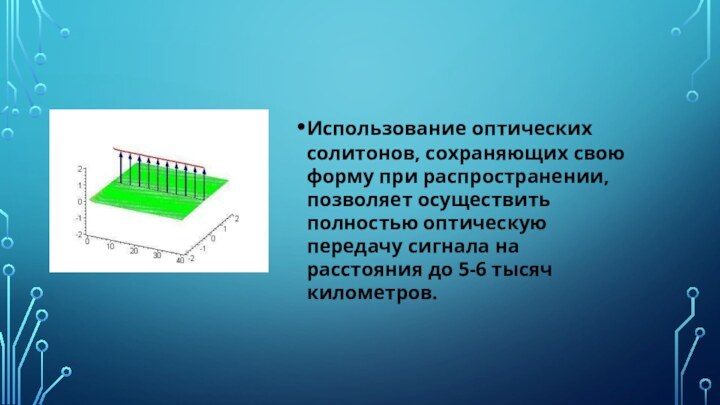
Использование оптических солитонов, сохраняющих свою форму при распространении,
позволяет осуществить полностью оптическую передачу сигнала на расстояния до
5-6 тысяч километров.
Слайд 17
В геноме человека находятся так называемые голографические солитоны,
представляющие собой полевые (волновые) многомерные энергоинформационные структуры, свидетельствующие о
сосредоточении большого количества энергии в очень малом объёме пространства, мигрирующие как внутри физического тела, так и за его пределами, и вызывающие различные функциональные расстройства.
Слайд 18
Хаос – высшая степень порядка. Хаос (греч. Chaos)
– 1)в греческой мифологии и философии: беспредельное пространство (представляющее
собой беспорядочную смесь материальных элементов мира), из которого произошло всё материальное. 2)крайний беспорядок, неразбериха. Что же понятие «Хаос» означает теперь?
Слайд 19
Теория хаоса математический аппарат, описывающий поведение некоторых
нелинейных динамических систем, подверженных, при определённых условиях, явлению, известному
как хаос, которое характеризуется сильной чувствительностью поведения системы к начальным условиям.
Слайд 20
Первая хаотическая система, обнаруженная Лоренцем, точно соответствует механическому
устройству – водяному колесу, которое ведёт себя очень сложным
образом
Слайд 21
Аттракторами часто называют режим движения к которому стремится
со временем эволюция динамической системы. Например, вырожденным, но достаточно
типичным случаем предельного режима движения является состояние покоя, когда аттрактор представляет собой точку в фазовом пространстве. Такой аттрактор есть, например, в системе пружинного маятника с трением о воздух.
Слайд 22
Странный Аттрактор - уже из четвертого измерения, самоорганизующийся.
То, что поверхностный взгляд воспринимает как абсолютный Хаос, в
котором не заметно никакого порядка, имеет определенный порядок, базирующийся на Странном Аттракторе, если наблюдение ведется из четвертого измерения. Четырехмерность Странного Аттрактора получается за счет добавления пульсаций (вибраций). Важнейшей характеристикой Странного Аттрактора является чувствительность к начальным условиям («Эффект бабочки»).
Слайд 23
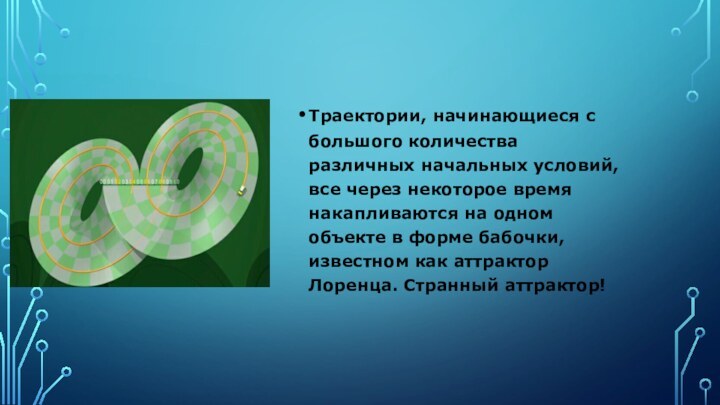
Траектории, начинающиеся с большого количества различных начальных условий,
все через некоторое время накапливаются на одном объекте в
форме бабочки, известном как аттрактор Лоренца. Странный аттрактор!