Презентация на тему Определение критериев физического подобия для механической системы

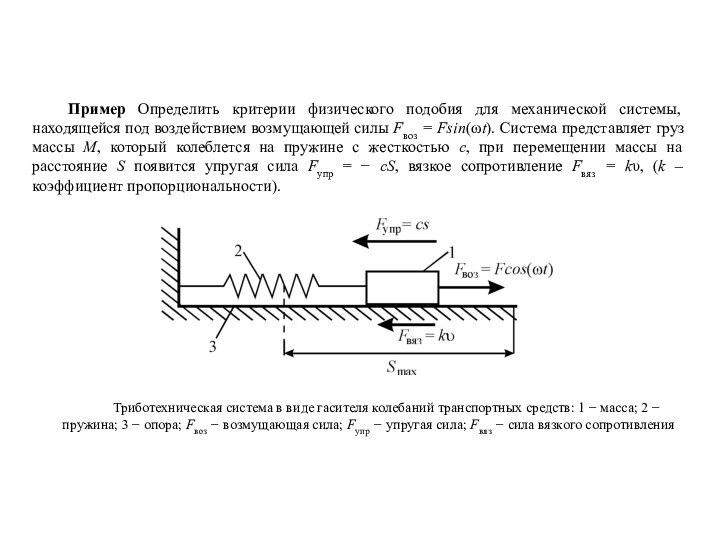
гасителя вертикальных колебаний.

1. Выявляем параметры, которые определяют процесс колебания

механической системы:
1)P1 – М (кг), 2) Р2 – ω (с−1), 3) Р3 – F (кг⋅м/с2),
4) Р4 – S (м), 5) P5 – μ (кг/с), 6) P6 − c (кг/с2),
7) P7 − t (c).

Участвующих величин будет семь (m = 7). Функциональная зависимость, подлежащая исследованию, получит вид:
Ф(Р1, Р2, Р3, Р4, Р5, Р6, Р7) = 0 или Ф(М, ω, F, S, μ, с, t) = 0, где Р1, Р2 ,…, Р7 − параметры системы.

2. Выберем три (k = 3) независимые единицы применительно к системе измерений LMT (здесь L – линейный размер, м; М − масса, кг; Т − время, с). В качестве основных (базисных) параметров примем: P1 = М, кг; Р2 = ω, с−1, P3 = F, кг⋅м/с2.

P1 = [M] =

[L]0 [M]1 [T]0,
P2 = [ω] = [L]0 [M]0 [T]−1,
P3 = [F] = [L]1 [M]1 [T]−2.

Остальные четыре параметра (Ni − k = 7 − 4 = 3) уравнения примут вид

P4 = [S] = [L]1 [M]0 [T]0,
P5 = [μ] = [L]0 [M]1 [T]−1,
P6 = [c] = [L]0 [M]1 [T]−2,
P7 = [t] = [L]0 [M]0 [T]1.

4. Проверяем правильность сделанного выбора по числу независимых (базисных) параметров (k = 3), составив матрицу размерностей

Используя формулы Крамера

параметров р1, р2, р3 и их количество (k =

3) выбрано правильно и величины М, ω, F действительно независимы.

Определитель D = 0 принимается в частных случаях, например, при использовании в опытах одинаковых материалов как для модели, так и образца, т. е. Сλ = Сμ = СТ = СНВ = 1 или λм = λ0, μм = μ0, Ем = Е0, НВм = НВ0 и т.д. (здесь λ – теплопроводность; μ – коэффициент Пуассона; Е – модуль упругости; НВ – твердость материала)

− k критериев подобия. В общем виде их можно

записать в виде дробей:

Нахождение критериев подобия заключается в отыскании значений показателей степени.

могут быть найдены из определителя D1-3 после

замены в нем i-строки на строку, составленную из показателей степени αS,μ,c,t , βS, μ,c,t , εS, μ,c,t величин p4, p5, p6, p7 взятых из формулы:

6. Определяются значения показателей степени α, β, ε.

запишем в следующем виде:

Так как ω = 1/Т, то

действием сил представляется функциональной зависимостью из критериев подобия

Ф(π4; π5; π6; π7) = 0

или

приняты масса М, длина L, время Т, температура θ,

а за независимые параметры – σ – напряжение; t – время; l – длина; ϑ – температура.

Cоставим систему уравнений размерностей всех величин
ln [a] = 0 ln M + 2 ln L – ln T + 0 ln θ,
ln [σ] = ln M – ln L – 2 ln T + 0 ln θ,
ln [t] = 0 ln M + 0 ln L + ln T + 0 ln θ,
ln [l] = 0 ln M + ln L + 0 ln T + 0 ln θ,
ln [ϑ] = 0 ln M + 0 ln L + 0 ln T + ln θ.