- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Определение напряжений на различных площадках
Содержание
- 2. Напряжения на наклонных площадках
- 3. Элементарный объём в форме параллепипеда, связанный с
- 4. Положение наклонной площадки характеризуется вектором нормали
- 5. Составим уравнение равновесия сил в проекции на
- 6. Чтобы определить нормальное напряжение на наклонной площадке,
- 7. С учетом закона парности касательных напряжений (yx=
- 8. Главные площадки и главные напряжения
- 9. Нормальные и касательные напряжения на наклонной площадке
- 10. Предположим, что наклонная площадка с направляющими косинусами
- 11. Проекции по координатным осям:Px = xl +
- 12. Система уравнений имеет ненулевое решение (нулевое не
- 13. Сгруппируем слагаемые по степеням главного напряжения- 3
- 14. Введенные обозначения называются инвариантами напряженного состояния. Так
- 15. Виды напряженных состояний в точке
- 16. Объемное (трехосное) напряженное состояниеI10, I20, I30, следовательно
- 17. Примеры различных видов напряженных состояний
- 18. Объемное- возникает во время объемной штамповки
- 19. Плоское-возникает при изгибе или изгибе с кручением
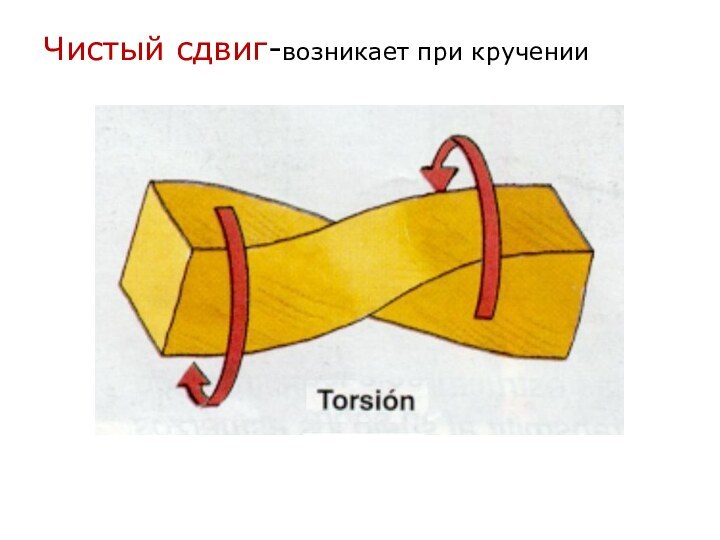
- 20. Чистый сдвиг-возникает при кручении
- 21. Линейное- возникает при растяжении-сжатии
- 22. Экстремальные свойства главных напряжений. Круговая диаграмма Мора
- 23. = 1l2 + 2m2 + 3n2
- 24.
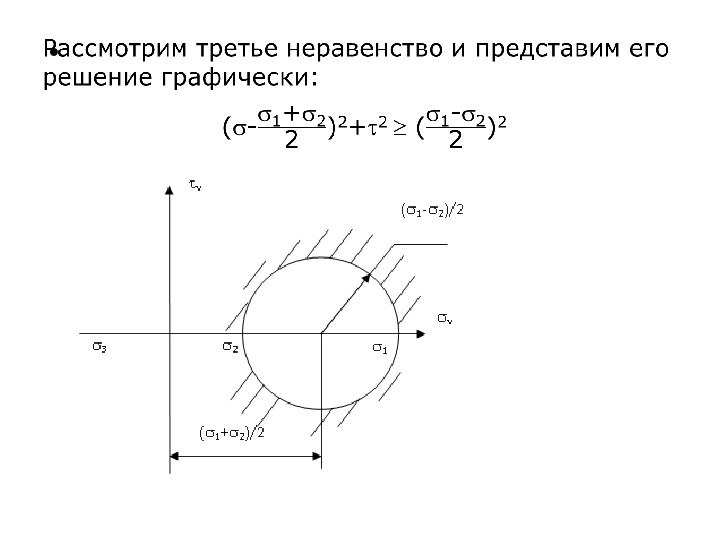
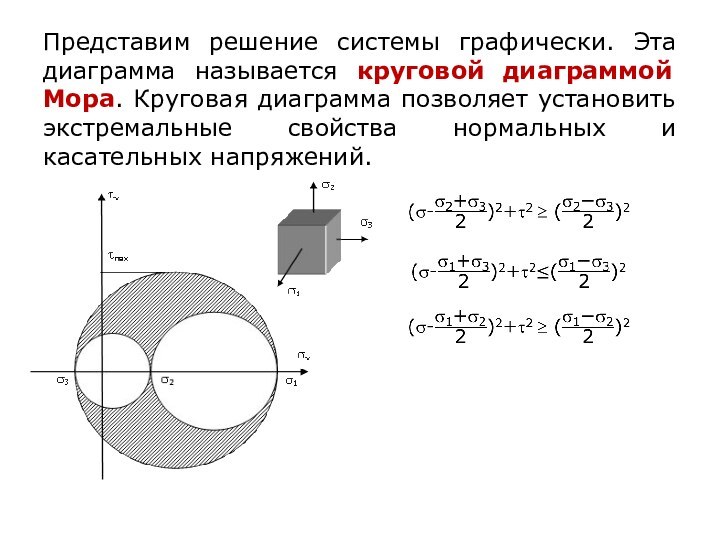
- 29. Представим решение системы графически. Эта диаграмма называется
- 30. Скачать презентацию
- 31. Похожие презентации
Напряжения на наклонных площадках


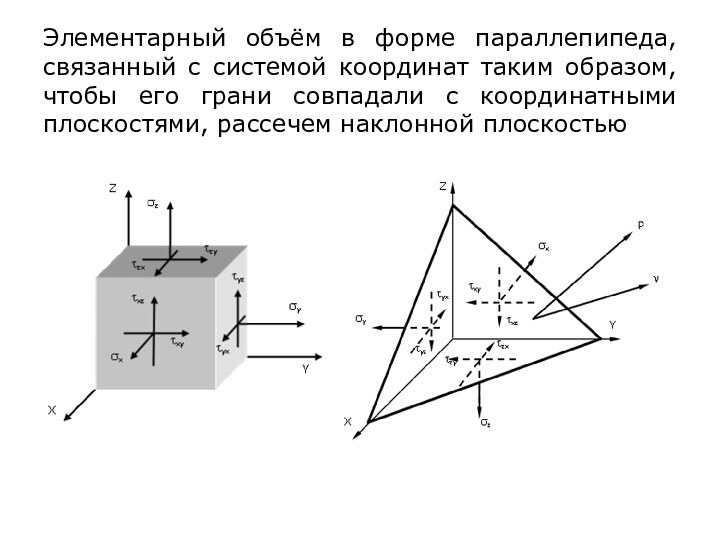















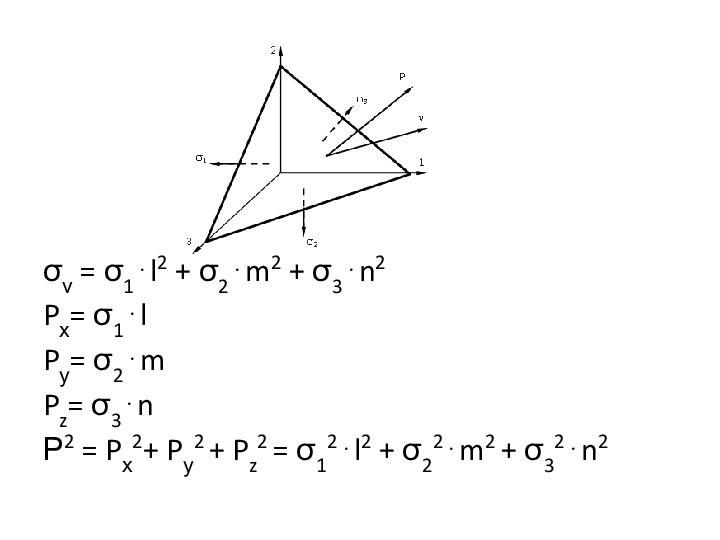




Слайд 4 Положение наклонной площадки характеризуется вектором нормали с
направляющими косинусами l, m, n. На наклонной площадке площадью
dF действует полное напряжение Р с проекциями по осям Рх, Ру, Рz. Пусть нормальные и касательные напряжения на гранях, совпадающих с координатными плоскостями, известны. Необходимо найти нормальное и касательное напряжение на наклонной площадке - и . Площадки, отсекаемые на координатных плоскостях, будут иметь площади:dFx = dFl, dFy = dFm, dFz = dFn.
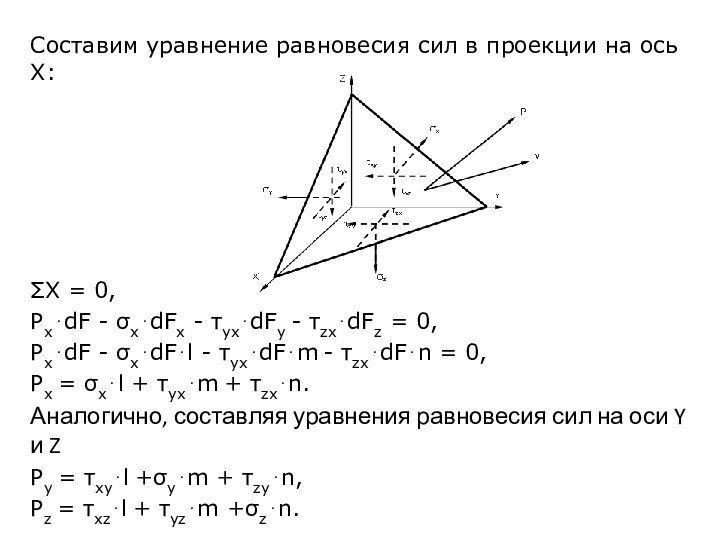
Слайд 5 Составим уравнение равновесия сил в проекции на ось
Х:
Х = 0,
PxdF - xdFx - yxdFy - zxdFz = 0,
PxdF - xdFl - yxdFm - zxdFn = 0,
Px = xl + yxm + zxn.
Аналогично, составляя уравнения равновесия сил на оси Y и Z
Py = xyl +ym + zyn,
Pz = xzl + yzm +zn.
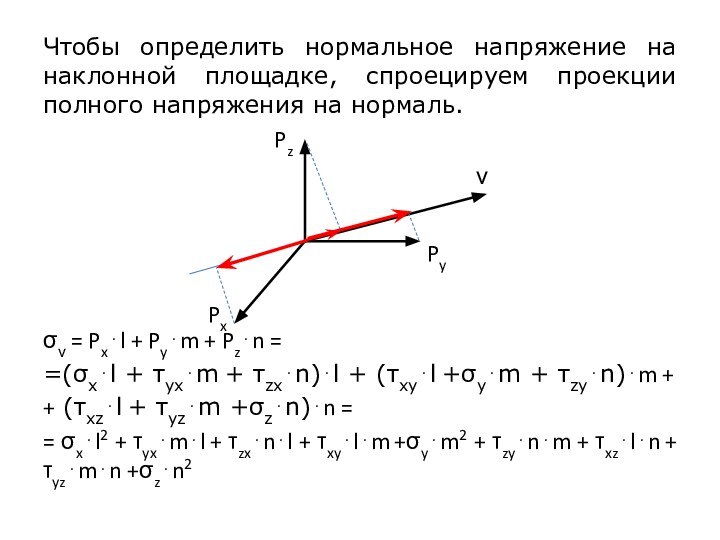
Слайд 6 Чтобы определить нормальное напряжение на наклонной площадке, спроецируем
проекции полного напряжения на нормаль.
= Pxl + Pym
+ Pzn ==(xl + yxm + zxn)l + (xyl +ym + zyn)m +
+ (xzl + yzm +zn)n =
= xl2 + yxml + zxnl + xylm +ym2 + zynm + xzln + yzmn +zn2
Px
Py
Pz
Слайд 7 С учетом закона парности касательных напряжений (yx= xy,
yz= zy, zx= xz), получаем основную квадратичную форму нормальных
напряжений: = xl2 + ym2 +zn2 + 2yxml + 2zxnl + 2zynm
Полученное выражение позволяет определить нормальное напряжение на любой наклонной площадке, поскольку при выводе этого выражения никаких ограничений на положение площадки не накладывалось. Теперь найдем величину касательного напряжения на наклонной площадке:
Р2 = Px2 + Pу2+ Pz2 = 2 + 2,
2= Px2 + Pу2+ Pz2 - 2.
Слайд 9 Нормальные и касательные напряжения на наклонной площадке зависят
от ее положения, то есть от направляющих косинусов l,
m, n.Площадки, на которых касательные напряжения равны нулю и действуют только нормальные напряжения, называются главными. Нормальные напряжения на этих площадках называются главными напряжениями.
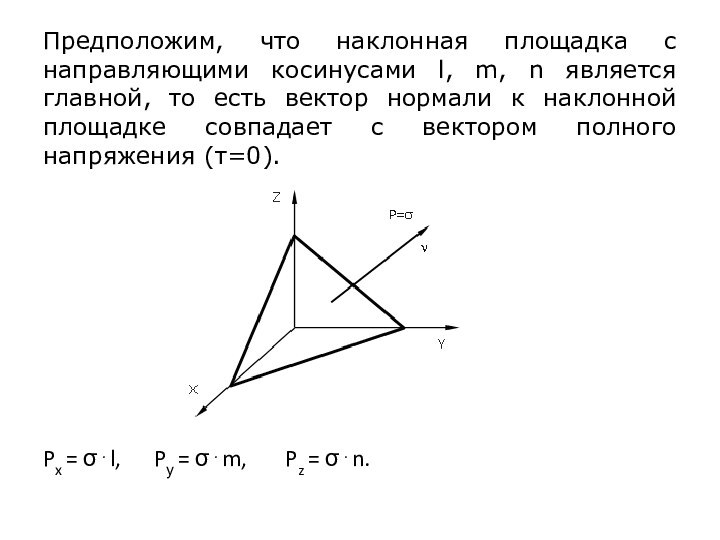
Предположим, что наклонная площадка с направляющими косинусами l, m, n является главной, то есть вектор нормали к наклонной площадке совпадает с вектором полного напряжения. Тогда нормальное напряжение на этой площадке равно полному напряжению, а касательное напряжение равно нулю.
Слайд 10 Предположим, что наклонная площадка с направляющими косинусами l,
m, n является главной, то есть вектор нормали к
наклонной площадке совпадает с вектором полного напряжения (=0).Px = l, Pу = m, Pz = n.
Слайд 11
Проекции по координатным осям:
Px = xl + yxm
+ zxn = l,
Pу = xyl + ym +
zyn = m, Pz = xzl + yzm + zn = n.
В данных уравнениях четыре неизвестных (направляющие косинусы l, m, n и главное напряжение ), поэтому необходимо четвертое уравнение:
(x - )l + yxm + zxn = 0
xyl + (y - )m + zyn = 0
xzl + yzm + (z - )n = 0
l2 + m2 + n2 = 1
Слайд 12 Система уравнений имеет ненулевое решение (нулевое не устраивает
из-за четвертого уравнения системы), когда равен нулю главный определитель
системы:x - yx zx
xy y - zy = 0
xz yz z -
Раскроем определитель
(x - )(y - )(z - ) + yxzyxz + xyyzzx - xz(y - )zx - xyyx(z - ) - yzzy(x - ) = 0.
Слайд 13
Сгруппируем слагаемые по степеням главного напряжения
- 3 +
2(x + y + z) - (yz + xz
+ xу - xz2 - xу2 - уz2) + (xyz + 2xyyzzx - yxz2 - zxу2 - - хуz2) = 0.Запишем это уравнение в более компактной форме
3 – I12 + I2 – I3 = 0
где I1 = x + y + z,
I2 = yz + xz + xу - xz2 - xу2 - уz2,
I3 = xyz + 2xyyzzx - yxz2 - zxу2 - хуz2
Слайд 14 Введенные обозначения называются инвариантами напряженного состояния. Так как
главные напряжения в точке являются физической характеристикой, то они
не зависят от выбора системы координат, а, следовательно, и значения инвариантов также не зависят от выбора системы координат.Решая кубическое уравнение, получим три вещественных корня – три главных напряжения, которые нумеруются в порядке убывания: 1 2 3. Подставляя величину главного напряжения в систему, можно определить положение главной площадки, т.е. определить ее направляющие косинусы. Три главных площадки в точке взаимно перпендикулярны.
Слайд 16
Объемное (трехосное) напряженное состояние
I10, I20, I30, следовательно три
главных напряжения отлично от нуля.
Плоское (двухосное) напряженное состояние
I10, I20,
I3=0, следовательно два главных напряжения отлично от нуля.Чистый сдвиг (частный случай плоского)
I1=0, I20, I3=0, следовательно два главных напряжения отлично от нуля (причем 1 =-3).
Линейное (одноосное) напряженное состояние
I10, I2=0, I3=0, следовательно одно главное напряжение отлично от нуля.
Слайд 23
= 1l2 + 2m2 + 3n2
Pх=
1l
Pу= 2m
Pz= 3n
Р2 = Pх2+ Pу2 + Pz2 =
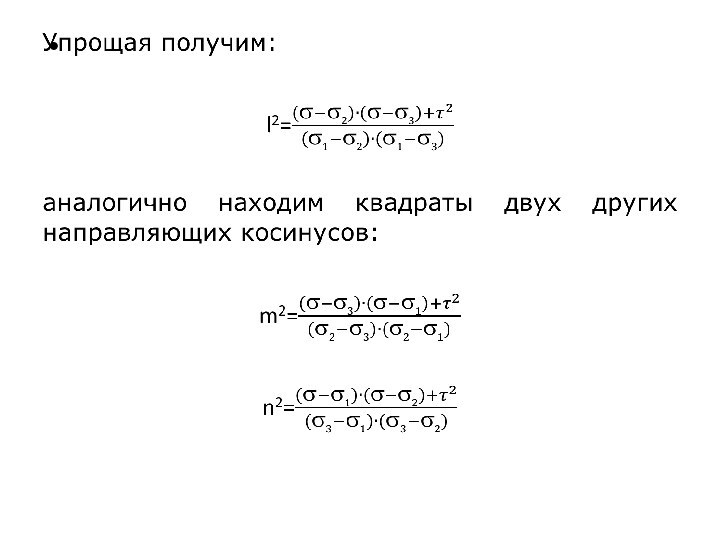
12l2 + 22m2 + 32n2 Слайд 24 =
1l2 + 2m2 + 3n2
2 + 2 = 12l2 + 22m2 + 32n21 = l2 + m2 + n2
Умножим каждое уравнение на произвольные множители a, b, c и сложим, сгруппировав при этом слагаемые по направляющим косинусам
а + b(2 + 2) + с =
= l2(а1 + b12 + с) + m 2(а2 + b22 + с) + +n2(а3 + b32 + с)





























