Презентация на тему Основные законы теории электромагнитного поля

взаимодействия между электрическими зарядами, теорема Гаусса,
закон БиоСавара, описывающий

магнитные поля, возбуждаемые движущимися электрическими зарядами и закон Ампера,
Сила Лоренца - сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу.
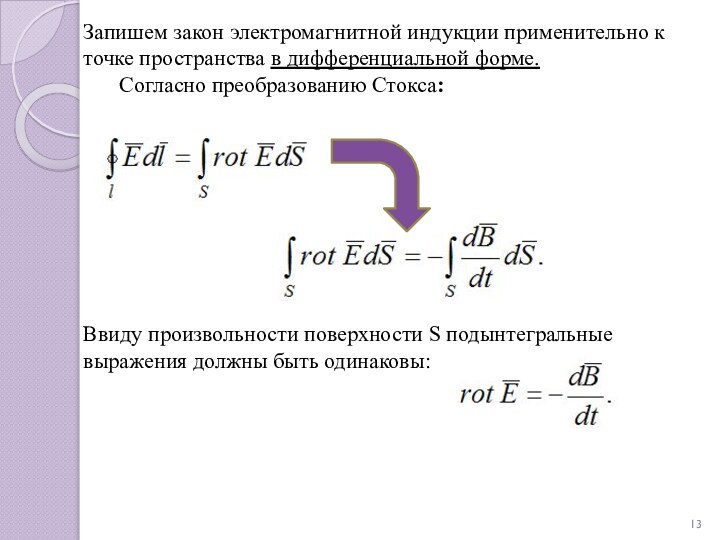
законы электромагнитной индукции Фарадея, согласно которым изменение магнитного потока порождает электрическое поле и индуцирует ток в проводниках (см. также Правило Ленца).
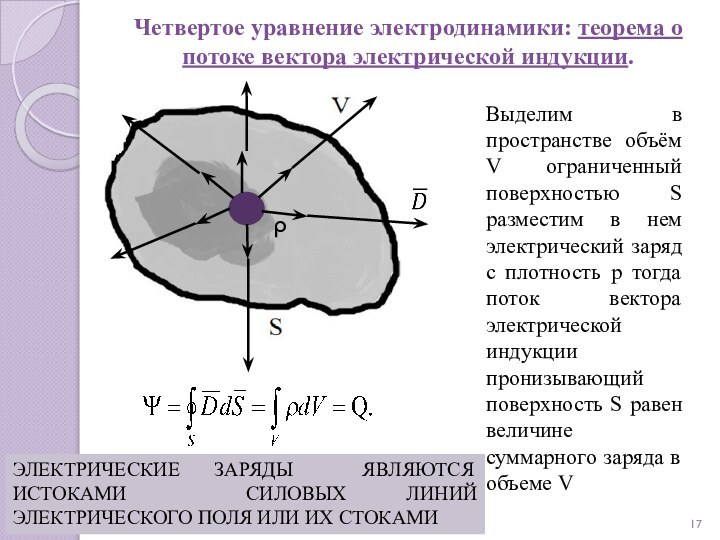
гипотеза об отсутствии в природе магнитных монополей.

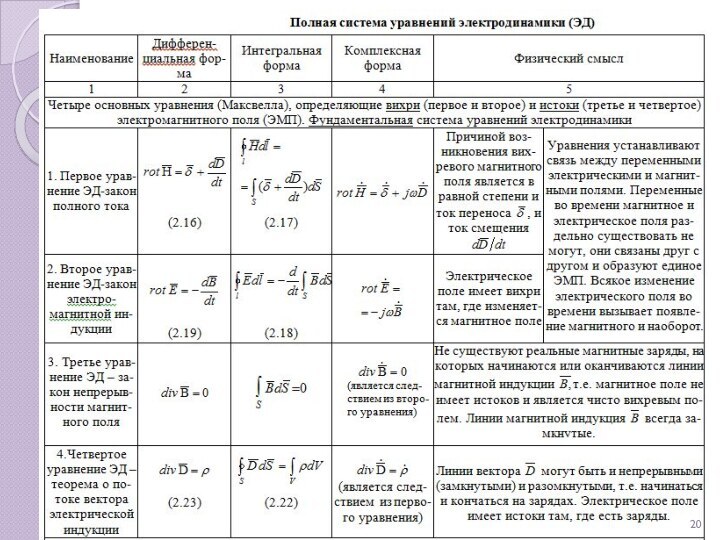
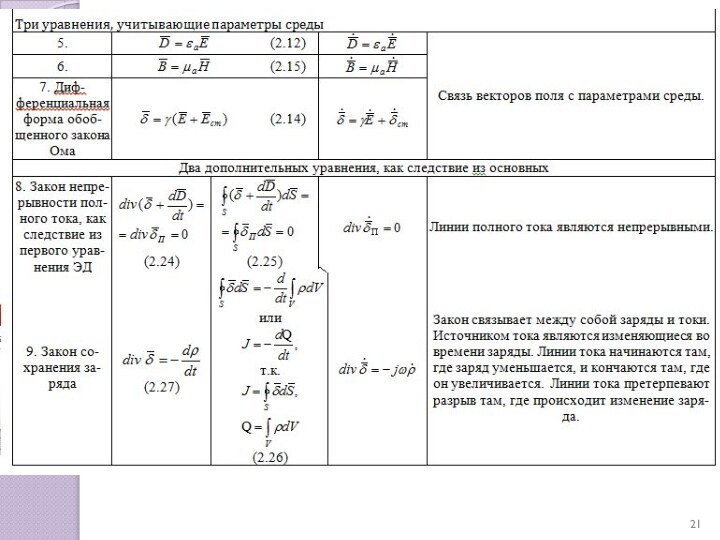
Уравнения, сформулированные Джеймсом Клерком Максвеллом, возникли на основе ряда важных экспериментальных открытий, которые были сделаны в начале XIX века.

магнитного поля и обобщая результаты опытов Эрстеда и Фарадея,

Максвелл создал теорию электромагнитного поля. Теория Максвелла – теория близкодействия, согласно которой электрические и магнитные взаимодействия распространяются со скоростью, равной скорости света в данной среде.

В основе теории Максвелла лежат два положения.
Всякое переменное электрическое поле порождает вихревое магнитное поле.

2. Всякое переменное магнитное поле порождает вихревое электрическое поле

и магнитных явлений.
Между пластинами конденсатора заряды не могут

перемещаться. Согласно Максвеллу, через конденсатор протекают токи смещения, причем в тех участках, где отсутствуют проводники.
Максвелл ввел понятие плотность тока смещения Рассмотрим, каково направление векторов плотностей токов проводимости и смещения. При зарядке конденсатора (рис.а) ток течет от правой обкладки к левой, поле в конденсаторе усиливается.

D- вектор электрического смещения (индукция)

(например, ионов или свободных электронов).
В случае, если этот

ток идёт не в веществе, а в свободном пространстве, нередко вместо термина
«ток проводимости» употребляют термин «ток переноса». Иначе говоря, ток переноса обусловлен переносом электрических зарядов в свободном пространстве заряженными частицами или телами под действием электрического поля.

В природе можно выделить два вида токов:
ток связанных зарядов и ток проводимости.

это перемещение средних положений связанных электронов и ядер, составляющих молекулу, относительно центра молекулы

пространстве не разделены, они находятся в одном и том

же объеме. Поэтому Максвелл ввёл понятие полного тока

Закон показывает, что причиной возникновения магнитного поля является в равной степени и ток переноса, и ток смещения, а также устанавливает количественную связь между током и магнитным полем.
Ток смещения называется током, потому что его действие такое же, как тока переноса. Физически ток смещения обнаруживается потому, что переменное электрическое поле вызывает появление магнитного поля.

плотность тока jk.
Электрический ток вызывает магнитное поле Н.
Выделим в

пространстве контур L на который опирается поверхность S. Величина тока который пронизывает эту поверхность равна интегралу плотности тока по поверхность S, количественную связь между величиной тока и напряженностью магнитного поля установил АМПЕР,

опытным путем он установил ток пронизывающий поверхность S равен циркуляции вектора напряженности магнитного поля по контуру L. Чтобы вычислить циркуляцию надо в каждой точки контура вектор напряженности поля скалярно умножить на векторный элемент дуги dl и проинтегрировать по контуру.

системы в некоторый момент времени
Построим поверхность S опирающийся на

контур L.

если уменьшать контур L стягивая в точку , циркуляция вектора магнитного поля будет стремиться к нулю, между тем амперметр в цепи конденсатора показывает , что ток втекает внутрь поверхность s ,таким образом интегралы не равны друг другу

S наружу вытекает такой же ток какой втекает во

внутрь тогда сумма токов будет равна нулю Максвелл назвал это ток смещения. Ток смещения связан с изменением во времени электрического поля и плотность его равна скорости изменения вектора электрической индукции D.

Мы получили закон полного тока (первое уравнение электродинамики) в интегральной форме.

Согласно этому закону, циркуляция вектора напряженности магнитного поля по замкнутому контуру равна полному току, протекающему сквозь поверхность, натянутую на этот контур

тока в дифференциальной форме ( для решения задач:
Согласно этому

закону, вихрь вектора напряженности магнитного поля в каждой точке равен объемной плотности полного тока в этой точке.

Для получения закона полного тока в интегральной форме проинтегрируем уравнение по произвольной поверхности S

Используя теорему Стокса о связи между интегралами по контуру и по поверхности

произвольный контур L
Изменение во времени магнитного поля вызывает появление

электрического
Обойдя контур определим ЭДС наводимую в нем, она равна скорости изменения магнитного потока пронизывающего площадь S контура взятую с обратным знаком

Количественная связь между скоростью изменения магнитной индукции и электрическим полем

в интегральной форме
магнитный поток (поток вектора магнитной индукции) через

поверхность S.

Согласно этому закону, меняющееся во времени магнитное поле вызывает независимо от параметров среды такое электрическое поле, что для всякого произвольного контура циркуляция вектора напряженности этого поля равна взятой с обратным знаком скорости увеличения магнитного потока через поверхность, ограниченную этим контуром.

в дифференциальной форме.
Согласно преобразованию Стокса:

Ввиду произвольности поверхности S подынтегральные

выражения должны быть одинаковы:

В ПРИРОДЕ НЕ СУЩЕСТВУЮТ И СИЛОВЫЕ ЛИНИИ МАГНИТНОГО ПОЛЯ

ЗАМКНУТЫ САМИ НА СЕБЯ

магнитного поля в интегральной форме:
Согласно этому закону, магнитный поток

сквозь замкнутую повер­хность равен нулю. Для того чтобы получить этот закон в дифферен­циальной форме, используем преобразование Остроградского-Гаусса

Так как объем V произволен, то подынтегральное выражение равно нулю

дифференциальной форме. Он показывает, что магнитное поле не имеет

истоков. Линии индукции магнитного поля всегда замкнутые.
Закон непрерывности справедлив для любых полей в любой среде, потому что в любой среде индукции поля учитывают и внешнее, и наведенное поле.

индукции.

Выделим в пространстве объём V ограниченный поверхностью S разместим

в нем электрический заряд с плотность р тогда поток вектора электрической индукции пронизывающий поверхность S равен величине суммарного заряда в объеме V

V

ρ

 

ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ ЯВЛЯЮТСЯ ИСТОКАМИ СИЛОВЫХ ЛИНИЙ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ИЛИ ИХ СТОКАМИ

индукции.

Теорема о потоке вектора электрической индукции в интегральной форме:

Согласно

этой теореме, поток вектора электрической индукции через замкнутую поверхность равен суммарному свободному заряду Q, который находится в объеме, ограниченном этой поверхностью.
Для того чтобы получить эту теорему в дифференциальной форме, используем преобразование Остроградского-Гаусса. С учетом произвольности объема получим эту теорему в следующем виде:

объемной плотности свободных зарядов в каждой точке поля. Источниками

вектора электрической индукции являются только свободные заряды. Поэтому введение вектора позволяет получить очень удобные соотношения между полем и зарядами, в которых не фигурирует поляризация среды. Силовые линии электрического поля начинаются на положительных зарядах и оканчиваются на отрицательных.

Из этих уравнений следует, что электромагнитное поле представляет собой

особую форму материи, характерную тем, что она осуществляет взаимодействие электрических зарядов и связывает их в единую систему. Поле и заряды при этом выступают как формы проявления этой единой материальной системы.

Уравнения электродинамики определяют как законы взаимодействия поля и зарядов, так и внутренние свойства самого электромагнитного поля.

вытекает ряд важных выводов:
1. Существуют электромагнитные волны, то

есть распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы и перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны

Принцип распространения электромагнитной волны состоит в том, что вектора напряженности электрического и магнитного поля E и H колеблются в фазе, т.е. они достигают максимума и минимума в одних и тех же точках пространства

вдоль направления распространения плоской волны.
Фронт волны представляет собой

геометрическое место точек поля с одинаковой фазой: у плоской волны одной из этих поверхностей является плоскость , перпендикулярная направлению распространения волны. У плоской однородной волны поверхности равных фаз и равных амплитуд совпадают.

Любой волновой процесс характеризуется
длиной волны ,
коэффициентом фазы ,
фазовой и групповой скоростями.

между двумя точками поля бегущей волны, разность фаз которых

равна.
Фазовая скорость это скорость перемещения фронта волны. Фазовая скорость может быть больше скорости света, т.к. она не представляет собой скорости переноса энергии электромагнитного поля.

Монохроматическое поле характеризуется постоянной частотой , фазой и векторными амплитудами и .

Как известно, с помощью монохроматического колебания нельзя передавать информацию.
Передача информации неизбежно связана с модуляцией и спектром частот.
Если волной передается сигнал, который может быть представлен при помощи спектрального разложения в виде ряда или интеграла Фурье, то его можно считать суммой близких по частоте монохроматических волн.

, как скорости перемещения огибающей группы монохроматических волн,

близких между собой по частоте. Групповая скорость характеризует скорость перемещения весьма узкополосного сигнала и, следовательно, скорость перемещения энергии поля такого сигнала. Отсюда следует, что групповая скорость не может быть больше скорости света. На отдельные группы волн показаны пунктиром.

Коэффициент фазы показывает набег фазы бегущей волны на единицу длины.

с конечной скоростью, зависящей от свойств среды.
Свойства электромагнитных волн: -распространяются

не только в веществе, но и в вакууме; - распространяются в вакууме со скоростью; - это поперечные волны; - это бегущие волны (переносят энергию).

Источником электромагнитных волн являются ускоренно движущиеся электрические заряды. Колебания электрических зарядов сопровождаются электромагнитным излучением, имеющим частоту, равную частоте колебаний зарядов.