Презентация на тему Коды и антиподы

полезный сигнал и затрудняющее его приём. Ниже приведена

Внешние источники помех вызывают в основном импульсные помехи, а внутренние – флуктуационные

связано с добавлением к сходной комбинации (k-символов) контрольных (r-символов).

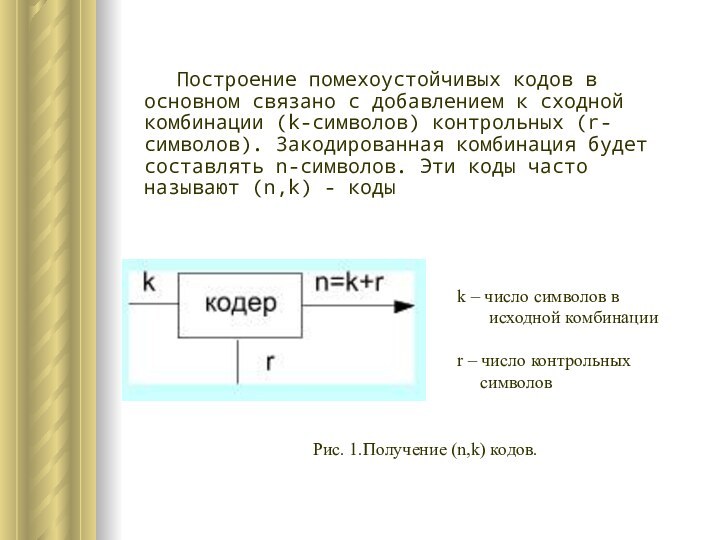
k – число символов в
исходной комбинации

r – число контрольных
символов

Рис. 1.Получение (n,k) кодов.

путём добавления к передаваемой комбинации, состоящей из k информационных

Пример 1. Построим коды для проверки на чётность, где k – исходные комбинации, r контрольные символы.

1. Код с проверкой на чётность.

обнаружения ошибок будет равна
Так как вероятность ошибок p

Вероятность появления всевозможных ошибок, как обнаруживаемых так и не обнаруживаемых, равна
, где - вероятность отсутствия искажений в кодовой комбинации. Тогда .

При передаче большого количества кодовых комбинаций , число кодовых комбинаций, в которых ошибки обнаруживаются, равно:

не обнаруживаемыми ошибками равно
Тогда коэффициент обнаружения для кода

Например, для кода с k=5 и вероятностью ошибки
коэффициент обнаружения составит . То есть 90% ошибок обнаруживаем, при этом избыточность будет составлять или 17%.

и нулей. Число кодовых комбинаций составит
2. Код с

Пример 2. Коды с двумя единицами из пяти и тремя единицами из семи.

Этот код позволяет обнаруживать любые одиночные ошибки и часть многократных ошибок. Не обнаруживаются этим кодом только ошибки смещения, когда одновременно одна единица переходит в ноль и один ноль переходит в единицу, два ноля и две единицы меняются на обратные символы и т.д.

этого кода возможны смещения трёх типов.
Вероятность появления не обнаруживаемых

При p<<1 тогда

Вероятность появления всевозможных ошибок как обнаруживаемых, так и не обнаруживаемых будет составлять

. Тогда коэффициент обнаружения будет равен
Например, код при

Элементы данного кода заменяются двумя символами, единица «1» преобразуется

Вместо комбинации 1010011 передается 10011001011010. Ошибка обнаруживается в том случае, если в парных элементах будут одинаковые символы 00 или 11 ( вместо 01 и 10).

Например, при k=5, n=10 и вероятности ошибки . Но при этом избыточность будет
составлять 50%

Back 3

такая же комбинация по длине. В линию посылается удвоенное

Приём инверсного кода осуществляется в два этапа. На первом этапе суммируются единицы в первой основной группе символов. Если число единиц чётное, то контрольные символы принимаются без изменения, если нечётное, то контрольные символы инвертируются. На втором этапе контрольные символы суммируются с информационными символами по модулю два.

При ненулевой сумме, принятая комбинация бракуется. Покажем суммирование для

Обнаруживающие способности данного кода достаточно велики. Данный код обнаруживает практически любые ошибки, кроме редких ошибок смещения, которые одновременно происходят как среди информационных символов, так и среди соответствующих контрольных. Например, k=5, n=10 и . Коэффициент обнаружения будет составлять .

угла поворота тела вращения в код. Принцип работы можно

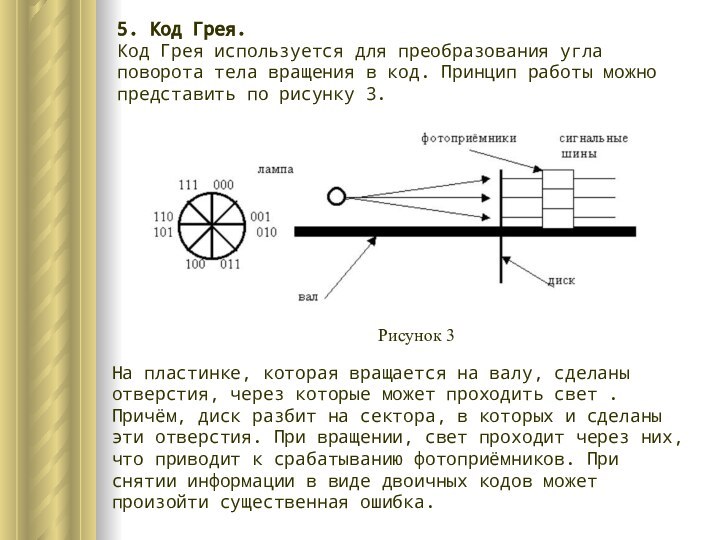
На пластинке, которая вращается на валу, сделаны отверстия, через которые может проходить свет . Причём, диск разбит на сектора, в которых и сделаны эти отверстия. При вращении, свет проходит через них, что приводит к срабатыванию фотоприёмников. При снятии информации в виде двоичных кодов может произойти существенная ошибка.

Рисунок 3

8. Двоичные коды этих цифр отличаются во всех разрядах.
Если

слева
направо, имеют положительный вес, а все чётные единицы

Разряды в коде Грея не имеют постоянного веса. Вес k-разряда определяется следующим образом

Например:

Непостоянство весов разрядов затрудняет выполнение арифметических операций в коде Грея, поэтому необходимо уметь делать перевод кода Грея в обычный двоичный код и наоборот. Алгоритм перевода чисел можно представить следующим образом.

Пусть - двоичный код, - код Грея.

Грея выполнится по следующему алгоритму:
Например:
Обратный переход из кода Грея

Например:

ошибки. Идею
представления корректирующих кодов можно
представить с помощью

Корректирующие коды

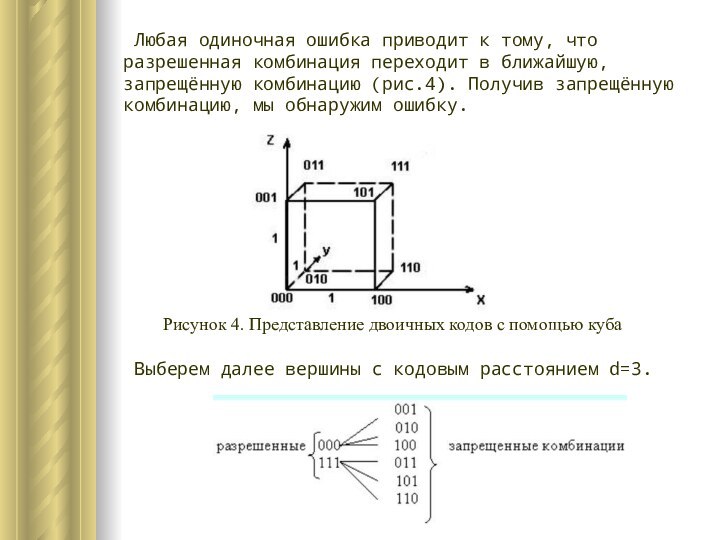
Возьмём трёхмерный куб (рис 4), длина рёбер, в котором равна одной единице.

Рисунок 4. Представление двоичных кодов с помощью куба

между вершинами определяется минимальным количеством рёбер, находящихся между вершинами.

Иначе, кодовое расстояние – это то минимальное число элементов, в которых одна кодовая комбинация отличается от другой.

Для определения кодового расстояния достаточно сравнить две кодовые комбинации по модулю 2. Так, сложив две комбинации

Определим, что расстояние между ними d=7.

комбинаций размещаются на вершинах трёхмерного куба. Такой код имеет

Если выберем комбинации с кодовым расстоянием d=2, например, 000, 110, 101, 011, то такой код позволит обнаруживать однократные ошибки. Назовём эти комбинации разрешенными, предназначенными для передачи информации. Все остальные 001, 010, 100,111 – запрещённые.

разрешенная комбинация переходит в ближайшую, запрещённую комбинацию (рис.4). Получив

Рисунок 4. Представление двоичных кодов с помощью куба

Выберем далее вершины с кодовым расстоянием d=3.

обнаружить две ошибки. Таким образом, увеличивая кодовое расстояние можно

Большинство корректирующих кодов являются линейными кодами.

Кроме того, корректирующие коды являются групповыми кодами.

1101 1110 0111 1011

2) 0000 1101 1110 0111 - не группа, так как не соблюдается условие замкнутости
( 1101 +1110 = 0011)

3) 000 001 010 011 100 101 110 111 - группа

Большинство корректирующих кодов образуются путём добавления к исходной k – комбинации r-контрольных символов. В итоге в линию передаются n=k+4 символов. При этом корректирующие коды называются (n,k) кодами. Как можно определить необходимое число контрольных символов?

ошибку необходимое число контрольных разрядов будет составлять
Это равносильно известной

Если необходимо исправить две ошибки, то число различных исходов будет составлять . Тогда

, в этом случае обнаруживаются однократные и двукратные ошибки. В общем случае, число контрольных символов должно быть не меньше

Хэмминга для числа контрольных символов.

1101101, 1001011.
2. Определить величину кодового расстояния d, обеспечивающего исправление