Презентация на тему Распределенные джозефсоновские переходы

Изменение фазы на длине dx
равно:

Здесь t =2λ+ ti – расстояние между электродами, “видимое” внешним магнитным полем Ве, а

погонные индуктивности электродов
с размерностью [Гн/м]

(1)

(2)

по координате, получим с учетом (1)
где
- джозефсоновская глубина

-погонная плотность критического тока

(3)

Переписав определение в виде

Замечаем, что это та длина, на которой приведенная индуктивность ячейки становится сравнимой с 1 и существенны эффекты самоиндукции

условий, следующих из (1) и (2)
(4)

(3) необходимо уравнение для джозефсоновского тока J:
где R0 [Ом

(5)

Найдем значение для перехода типа “сэндвич”

Если - индукция поля в зазоре, то

джозефсоновский ток не

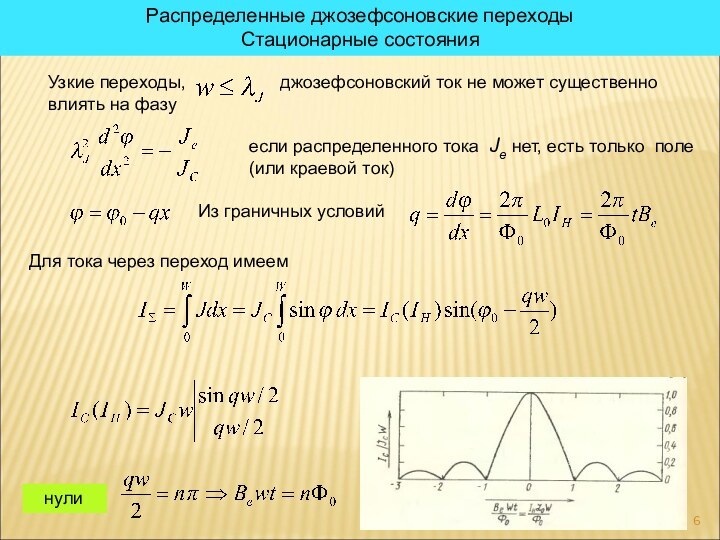
если распределенного тока Je нет, есть только поле
(или краевой ток)

Из граничных условий

Для тока через переход имеем

нули

ос Х порядка

(6)

(7)

(8)

длиной w, шириной w’ на единицу длины по направлению

где

поскольку

Во внешнем поле H0 потенциал Гиббса на единицу длины одного вихря