Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Реальные газы физика

Содержание

Реальные газыДля реальных газов наблюдается отклонение от закона К.-М., кроме того, при некоторых значениях внешних параметров они могут быть переведены в жидкое и даже твёрдое состояниеОтступление от законов идеального газа связаны с наличием межмолекулярного взаимодействия
Лекции по физике. Молекулярная физика и основы термодинамикиРеальные газы. Межмолекулярные взаимодействия. Низкие температуры Реальные газыДля реальных газов наблюдается отклонение от закона К.-М., кроме того, при Межмолекулярное взаимодействиеМежмолекулярные силы притяженияПоляризационные силы обусловлены несимметричностью распределения зарядов в нейтральной в Межмолекулярное взаимодействиеСилы притяжения обратно пропорциональны расстоянию в 7-й степениСилы отталкивания возрастают экспоненциально Межмолекулярное взаимодействиеВ уравнении Ван-дер-Ваальса применяется более грубая аппроксимация – молекулы считаются абсолютно Уравнение Ван-дер-ВаальсаУчтём влияние сил отталкивания. Конечный объём молекул приводит к уменьшению доступного Уравнение Ван-дер-ВаальсаТеперь учтём влияние сил притяжения. Оно проявляется в появлении избыточного давления: P+Pi=n⋅k⋅T, где Уравнение Ван-дер-Ваальса Уравнение Ван-дер-ВаальсаУчитывая совместное действие сил притяжения и отталкивания получим окончательно уравнение Ван-дер-Ваальса: (P+a/V2)⋅(V-b)=R⋅T для ν молей: (P+a⋅ν2/V2)⋅(V/ν-b)=R⋅T или: (P+a⋅ν2/V2)⋅(V-ν⋅b)=ν⋅R⋅T Другие уравнения состоянияУравнение Дитеричи: P⋅(V-b)=R⋅T⋅exp(-a/[R⋅T⋅V]) в пределе b Другие уравнения состоянияУравнение Бертло: (P+a/(Т⋅V2))⋅(V-b)=R⋅TУравнение Клаузиуса: здесь улучшение достигается за счёт введения третьего параметра Другие уравнения состоянияУравнение Камерлинг-Оннеса: P⋅V=R⋅T(1+B2(T)/V+B3(T)/V2+…), где В2, В3, …- второй, третий и т.д. вириальные Изотермы Ван-дер-ВаальсаУравнение В.д.В. Можно привести к виду: P⋅V3-(R⋅T+P⋅b)⋅V2+a⋅V-a⋅b=0 (*) это кубическое уравнение относительно V при Изотермы Ван-дер-ВаальсаПриравнивая коэффициенты при одинаковых степенях V, получим: Рк⋅Vк3=a⋅b, 3Рк⋅Vк2=a, 3Рк⋅Vк=R⋅Tк+Pк⋅bИз этих трёх уравнений Изотермы Ван-дер-ВаальсаРасхождение экспериментальных и теоретических значений свидетельствует о неточности уравнения В.д.В. Изотермы реальных газовНа изотермах реальных газов нет участка с (∂P/∂V)>0. Это неустойчивое Изотермы реальных газовL-B – перегретая жидкостьA-G – переохлаждённый парПравило Максвелла: реальная изотерма Перегретая жидкость Изотермы реальных газовНиже кривой АКS находится двухфазная область, а выше - однофазнаяОт Критическое состояние Изотермы реальных газовПравило рычагаПусть состояние газа характеризуется точкой М в двухфазной области Насыщенный пар Внутренняя энергия газа В.д.В.Для однофазных состояний: Эффект Джоуля-ТомсонаЭффект Джоуля-Томсона заключается в изменении температуры газа при его прохождении через Эффект Джоуля-ТомсонаПри b=0, а≠0 газ всегда охлаждаетсяПри b≠0, а=0 – всегда нагреваетсяСуществует Методы получения низких температурИспарение жидкостиЭффект Джоуля-ТомсонаАдиабатическое расширение газаРастворение одного вещества в другомПри Свойства веществ при низких температурах Конец лекции
Слайды презентации

Слайд 2 Реальные газы
Для реальных газов наблюдается отклонение от закона

Реальные газыДля реальных газов наблюдается отклонение от закона К.-М., кроме того,

К.-М., кроме того, при некоторых значениях внешних параметров они

могут быть переведены в жидкое и даже твёрдое состояние
Отступление от законов идеального газа связаны с наличием межмолекулярного взаимодействия

Слайд 3 Межмолекулярное взаимодействие
Межмолекулярные силы притяжения
Поляризационные силы обусловлены несимметричностью распределения

Межмолекулярное взаимодействиеМежмолекулярные силы притяженияПоляризационные силы обусловлены несимметричностью распределения зарядов в нейтральной

зарядов в нейтральной в целом молекуле
Дисперсионные силы обусловлены появлением

наведённой поляризации при сближении молекул
Силы отталкивания возникают на малых расстояниях из-за взаимного перекрытия электронных оболочек молекул. Они имеют квантовую природу

Слайд 4 Межмолекулярное взаимодействие
Силы притяжения обратно пропорциональны расстоянию в 7-й

Межмолекулярное взаимодействиеСилы притяжения обратно пропорциональны расстоянию в 7-й степениСилы отталкивания возрастают

степени
Силы отталкивания возрастают экспоненциально при уменьшении расстояния
Взаимодействие молекул удобно

описывать потенциальной энергией взаимодействия U(r)
Потенциал Леннарда-Джонса:
U(r)=a1/r12-a2/r6,
где a1 и a2 - константы

Слайд 5 Межмолекулярное взаимодействие
В уравнении Ван-дер-Ваальса применяется более грубая аппроксимация

Межмолекулярное взаимодействиеВ уравнении Ван-дер-Ваальса применяется более грубая аппроксимация – молекулы считаются

– молекулы считаются абсолютно твёрдыми шарами с диаметром d
d

является нечётко определённым параметром

Слайд 6 Уравнение Ван-дер-Ваальса
Учтём влияние сил отталкивания. Конечный объём молекул

Уравнение Ван-дер-ВаальсаУчтём влияние сил отталкивания. Конечный объём молекул приводит к уменьшению

приводит к уменьшению доступного объёма и увеличению давления по

сравнению с идеальным газом. Для одного моля запишем:
P⋅(V-b)=R⋅T,
где b – объём одного моля молекул газа

Слайд 7 Уравнение Ван-дер-Ваальса
Теперь учтём влияние сил притяжения. Оно проявляется

Уравнение Ван-дер-ВаальсаТеперь учтём влияние сил притяжения. Оно проявляется в появлении избыточного

в появлении избыточного давления:
P+Pi=n⋅k⋅T,
где Pi – избыточное «внутреннее» давление:
Pi=,
где

Nb – число молекул в пристеночном слое, отнесённое к единице площади, f – сила, действующая со стороны объёма газа
Nb~1/V, f~1/V → Pi=a/V2,
где а - константа

Слайд 8 Уравнение Ван-дер-Ваальса

Уравнение Ван-дер-Ваальса

Слайд 9 Уравнение Ван-дер-Ваальса
Учитывая совместное действие сил притяжения и отталкивания

Уравнение Ван-дер-ВаальсаУчитывая совместное действие сил притяжения и отталкивания получим окончательно уравнение Ван-дер-Ваальса: (P+a/V2)⋅(V-b)=R⋅T для ν молей: (P+a⋅ν2/V2)⋅(V/ν-b)=R⋅T или: (P+a⋅ν2/V2)⋅(V-ν⋅b)=ν⋅R⋅T

получим окончательно уравнение Ван-дер-Ваальса:
(P+a/V2)⋅(V-b)=R⋅T
для ν молей:
(P+a⋅ν2/V2)⋅(V/ν-b)=R⋅T
или:
(P+a⋅ν2/V2)⋅(V-ν⋅b)=ν⋅R⋅T

Слайд 10 Другие уравнения состояния
Уравнение Дитеричи:
P⋅(V-b)=R⋅T⋅exp(-a/[R⋅T⋅V])
в пределе b

Другие уравнения состоянияУравнение Дитеричи: P⋅(V-b)=R⋅T⋅exp(-a/[R⋅T⋅V]) в пределе b

a

является полуэмпирическим. При умеренных давлениях оно лучше чем уравнение В.д.В., но зато при высоких давлениях совершенно непригодно

Слайд 11 Другие уравнения состояния
Уравнение Бертло:
(P+a/(Т⋅V2))⋅(V-b)=R⋅T
Уравнение Клаузиуса:



здесь улучшение достигается

Другие уравнения состоянияУравнение Бертло: (P+a/(Т⋅V2))⋅(V-b)=R⋅TУравнение Клаузиуса: здесь улучшение достигается за счёт введения третьего параметра

за счёт введения третьего параметра

Слайд 12 Другие уравнения состояния
Уравнение Камерлинг-Оннеса:
P⋅V=R⋅T(1+B2(T)/V+B3(T)/V2+…),
где В2, В3, …- второй,

Другие уравнения состоянияУравнение Камерлинг-Оннеса: P⋅V=R⋅T(1+B2(T)/V+B3(T)/V2+…), где В2, В3, …- второй, третий и т.д.

третий и т.д. вириальные коэффициенты
Уравнение состояния любого газа может

быть приведено к данному виду

Слайд 13 Изотермы Ван-дер-Ваальса
Уравнение В.д.В. Можно привести к виду:
P⋅V3-(R⋅T+P⋅b)⋅V2+a⋅V-a⋅b=0 (*)
это кубическое

Изотермы Ван-дер-ВаальсаУравнение В.д.В. Можно привести к виду: P⋅V3-(R⋅T+P⋅b)⋅V2+a⋅V-a⋅b=0 (*) это кубическое уравнение относительно V

уравнение относительно V при некоторых P и T имеет

три корня, а в некоторой области P и T – один
В критической точке, где все корни равны:
P⋅V3-(R⋅T+P⋅b)⋅V2+a⋅V-a⋅b=Рк(V-Vк)3=0

Слайд 14 Изотермы Ван-дер-Ваальса
Приравнивая коэффициенты при одинаковых степенях V, получим:
Рк⋅Vк3=a⋅b, 3Рк⋅Vк2=a,

Изотермы Ван-дер-ВаальсаПриравнивая коэффициенты при одинаковых степенях V, получим: Рк⋅Vк3=a⋅b, 3Рк⋅Vк2=a, 3Рк⋅Vк=R⋅Tк+Pк⋅bИз этих трёх

3Рк⋅Vк=R⋅Tк+Pк⋅b
Из этих трёх уравнений можно найти:
Vк=3b, Рк=a/27b2, Тк=8a/(27R⋅b)
Отношение Kк=R⋅Tк/(Рк⋅Vк)=8/3=2,67 называется

критическим коэффициентом
Для одного моля идеального газа Kк=R⋅T/(Р⋅V)=1
Для реальных газов Kк>8/3

Слайд 15 Изотермы Ван-дер-Ваальса
Расхождение экспериментальных и теоретических значений свидетельствует о

Изотермы Ван-дер-ВаальсаРасхождение экспериментальных и теоретических значений свидетельствует о неточности уравнения В.д.В.

неточности уравнения В.д.В.

Слайд 16 Изотермы реальных газов
На изотермах реальных газов нет участка

Изотермы реальных газовНа изотермах реальных газов нет участка с (∂P/∂V)>0. Это

с (∂P/∂V)>0. Это неустойчивое состояние
Область D-B – жидкое состояние

с малой сжимаемостью
Область А-Е – газообразное состояние
Область L-G – двухфазное состояние жидкость-пар

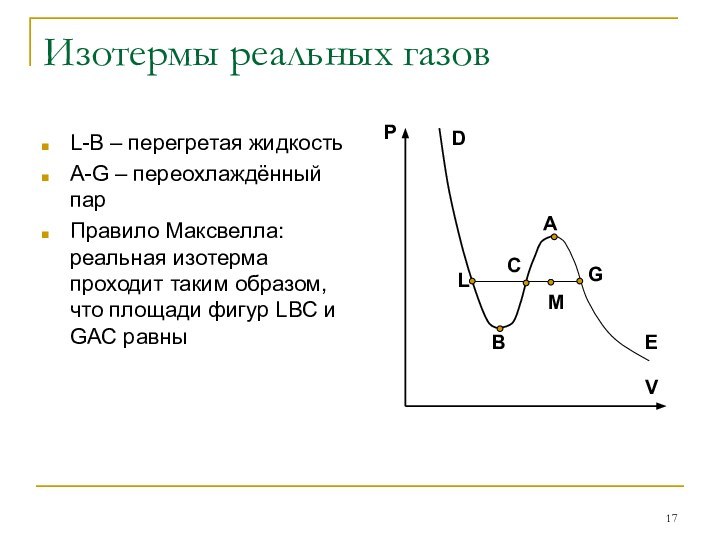
Слайд 17 Изотермы реальных газов
L-B – перегретая жидкость
A-G – переохлаждённый

Изотермы реальных газовL-B – перегретая жидкостьA-G – переохлаждённый парПравило Максвелла: реальная

пар
Правило Максвелла: реальная изотерма проходит таким образом, что площади

фигур LBC и GAC равны

Слайд 18 Перегретая жидкость

Перегретая жидкость

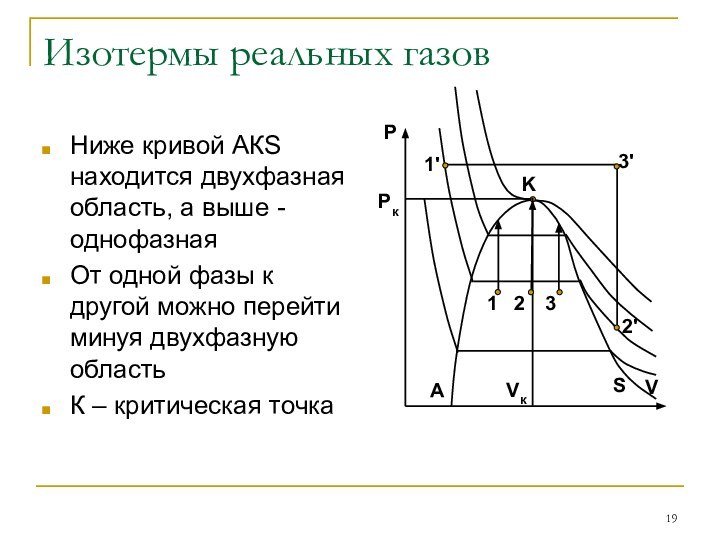
Слайд 19 Изотермы реальных газов
Ниже кривой АКS находится двухфазная область,

Изотермы реальных газовНиже кривой АКS находится двухфазная область, а выше -

а выше - однофазная
От одной фазы к другой можно

перейти минуя двухфазную область
К – критическая точка

Слайд 20 Критическое состояние

Критическое состояние

Слайд 21 Изотермы реальных газов
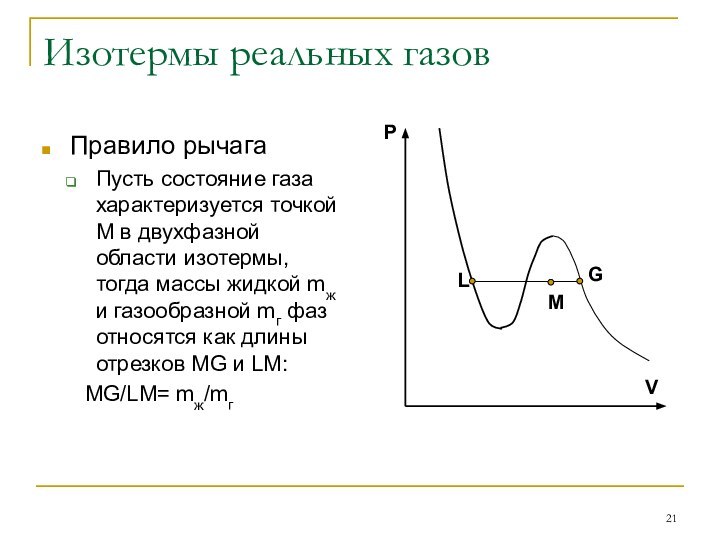
Правило рычага
Пусть состояние газа характеризуется точкой

Изотермы реальных газовПравило рычагаПусть состояние газа характеризуется точкой М в двухфазной

М в двухфазной области изотермы, тогда массы жидкой mж

и газообразной mг фаз относятся как длины отрезков MG и LM:
MG/LM= mж/mг

Слайд 22 Насыщенный пар

Насыщенный пар

Слайд 23 Внутренняя энергия газа В.д.В.
Для однофазных состояний:

Внутренняя энергия газа В.д.В.Для однофазных состояний:

Слайд 24 Эффект Джоуля-Томсона
Эффект Джоуля-Томсона заключается в изменении температуры газа

Эффект Джоуля-ТомсонаЭффект Джоуля-Томсона заключается в изменении температуры газа при его прохождении

при его прохождении через малое отверстие (дросселировании)
Для идеального газа

эффект отсутствует
Для реального газа эффект может быть как положительным (ΔТ/ΔР>0, газ охлаждается), так и отрицательным

Слайд 25 Эффект Джоуля-Томсона
При b=0, а≠0 газ всегда охлаждается
При b≠0,

Эффект Джоуля-ТомсонаПри b=0, а≠0 газ всегда охлаждаетсяПри b≠0, а=0 – всегда

а=0 – всегда нагревается
Существует температура инверсии Ti=(27/4)ТК при которой

эффект нулевой
Выше Ti газ нагревается при дросселировании, ниже Ti газ охлаждается
Для большинства газов Ti>>комнатной температуры
Для водорода и гелия Ti<<комнатной температуры

Слайд 26 Методы получения низких температур
Испарение жидкости
Эффект Джоуля-Томсона
Адиабатическое расширение газа
Растворение

Методы получения низких температурИспарение жидкостиЭффект Джоуля-ТомсонаАдиабатическое расширение газаРастворение одного вещества в

одного вещества в другом
При откачивании паров 3He можно получить

температуру 0,3 К
С помощью метода адиабатического размагничивания парамагнитных солей можно получить температуру ~10-3 К

Слайд 27 Свойства веществ при низких температурах

Свойства веществ при низких температурах
  • Имя файла: realnye-gazy-fizika.pptx
  • Количество просмотров: 237
  • Количество скачиваний: 3
- Предыдущая Животные на английском языке
Следующая - МОЙ ЛЮБИМЫЙ И РОДНОЙ ГОРОД КРАСНОДАР

Похожие презентации

Ворот-разновидность рычага Ворот-разновидность рычага 186
Физика и безопасность дорожного движения Физика и безопасность дорожного движения 141
Роль физиков в ВОВ Роль физиков в ВОВ 140
Подготовка к ЕГЭ Подготовка к ЕГЭ 165
Физика. Что изучает физика? Физика. Что изучает физика? 163
Мореплаватели и воздухоплаватели Мореплаватели и воздухоплаватели 118
Цепь Цепь 146
Люминесцентный анализ Люминесцентный анализ 156
Комп’ютерна томографія Комп’ютерна томографія 146
Презентация к уроку Линзы Презентация к уроку Линзы 115
Синхронды машина Синхронды машина 128
Техническая эксплуатация и ремонт теплообменника жесткой конструкции типа ТН, на установке УПН Техническая эксплуатация и ремонт теплообменника жесткой конструкции типа ТН, на установке УПН 145
Презентация к уроку физики 8 класс Агрегатные состояния вещества. Плавление и кристаллизация. Презентация к уроку физики 8 класс Агрегатные состояния вещества. Плавление и кристаллизация. 128
Презентация Развитие универсальных учебных действий (УУД) на уроках физики. Презентация Развитие универсальных учебных действий (УУД) на уроках физики. 184
Презетація по фізиці з'єднання конденсаторів Презетація по фізиці з'єднання конденсаторів 152
Электроизмерительные приборы и их применение Электроизмерительные приборы и их применение 143
Презентация: Измерение фокусного расстояния собирающей линзы. Получение изображений при помощи линзы Презентация: Измерение фокусного расстояния собирающей линзы. Получение изображений при помощи линзы 166
Джеймс Клерк Максвелл Джеймс Клерк Максвелл 142
Презентация по физике на тему механическое движение Презентация по физике на тему механическое движение 140
Правильное питание для детей Правильное питание для детей 137
Презентации к урокам физики Презентации к урокам физики 158
Свойства электромагнитных излучений Свойства электромагнитных излучений 118
Гальванический элемент Гальванический элемент 150
Электризация тел Электризация тел 143
Урок по физике на тему Тепловое движение. Температура (8 класс) Урок по физике на тему Тепловое движение. Температура (8 класс) 164
Урок-викторина по физике для 8-9 классов Урок-викторина по физике для 8-9 классов 191
Дифференциальный термометр сопротивления Дифференциальный термометр сопротивления 102
Влияние электромагнитного поля на организм человека Влияние электромагнитного поля на организм человека 124
Презентация по физике на тему Атомное ядро Презентация по физике на тему Атомное ядро 142
Магнитное поле и его географическое изображение. Магнитное поле и его географическое изображение. 138