- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
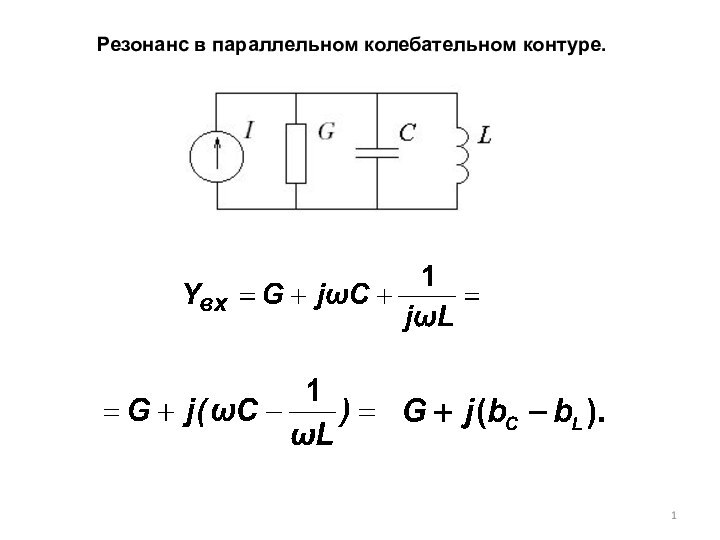
Презентация на тему Резонанс в параллельном резонансном контуре
Содержание
- 2. - резонансная частота контура.
- 3. Векторная диаграмма
- 4. Свойства параллельного колебательного контура.
- 5. Максимальное напряжение в момент резонанса:Добротность контура:
- 6. 5.9. Автоколебания Автоколебания происходят за счет
- 7. Пример механической автоколебательной системы
- 8. 5.10. Волновые процессы. Продольные и поперечные волныВолновым
- 9. Упругими волнами (или механическими) называются механические возмущения,
- 10. Гармонической упругой волной называется волна, если соответствующие
- 11. Волновым фронтом называется геометрическое место точек, до
- 12. Волна может быть плоской или сферической.Продольная плоская волнаПоперечная плоская волнаПродольная сферическая волнаПоперечная сферическая волна
- 13. Бегущими волнами называются волны, которые переносят в
- 14. Рассмотрим плоскую волну, предполагая,
- 15. Для характеристики волн используется волновое число:Фазовой скоростью
- 16. Уравнение сферической бегущей волны: r — расстояние
- 17. Распространение волн в однородной
- 18. 5.12. Интерференция волн.Когерентными называются волны, если разность
- 19. d1 и d2 — расстояния от источников
- 20. Условие максимума: разность хода волн равна целому
- 21. разность хода волн равна нечетному числу длин
- 22. Стоячие волны Другой частный случай
- 23. Сложим уравнения прямой и
- 24. Амплитуда стоячей волны изменяется
- 25. Координаты пучностей и узлов
- 26. Эффект Доплера. Доплер (1803-1853) – австрийский физик,
- 27. Длина звуковой волны:Период воспринимаемого наблюдателем звука:Связь длины
- 28. Случай 2. Источник движется. Наблюдатель неподвижен.Длина звуковой волны:Период воспринимаемого наблюдателем звука:Связь длины волны и частоты:
- 29. Частота звуковой волны, воспринимаемая наблюдателем:
- 30. Скачать презентацию
- 31. Похожие презентации


























Слайд 6
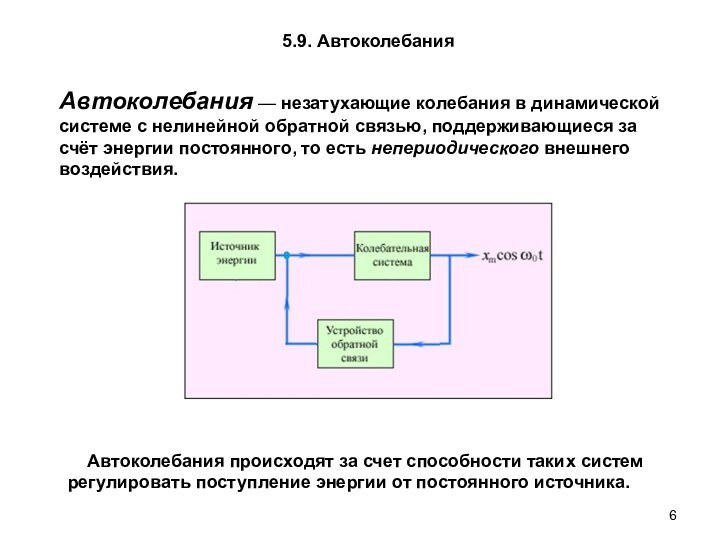
5.9. Автоколебания
Автоколебания происходят за счет способности
таких систем регулировать поступление энергии от постоянного источника.
незатухающие колебания в динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, то есть непериодического внешнего воздействия.Слайд 7 Пример механической автоколебательной системы –
часовой механизм с анкерным ходом.
Источник энергии –
поднятая вверх гиря или заведенная пружина. Колебательная система – маятник на подвесе.
Обратная связь – взаимодействие анкера с ходовым колесом.
Анкер позволяет ходовому колесу повернуться на один зубец за один полупериод.
Слайд 8
5.10. Волновые процессы. Продольные и поперечные волны
Волновым процессом
или волной называется процесс распространения колебаний в сплошной среде.
Основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.
Типы волн:
волны на поверхности жидкости,
упругие волны,
электромагнитные волны.
Слайд 9 Упругими волнами (или механическими) называются механические возмущения, распространяющиеся
в упругой среде.
Упругие волны бывают продольные и поперечные.
В продольных волнах частицы среды колеблются в направлении распространения волны,
В поперечных — в плоскостях, перпендикулярных направлению распространения волны.
Слайд 10 Гармонической упругой волной называется волна, если соответствующие ей
колебания частиц среды являются гармоническими.
Расстояние
между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны .Слайд 11 Волновым фронтом называется геометрическое место точек, до которых
доходят колебания к моменту времени t.
Волновой поверхностью называется геометрическое
место точек, колеблющихся в одинаковой фазе.
Слайд 12
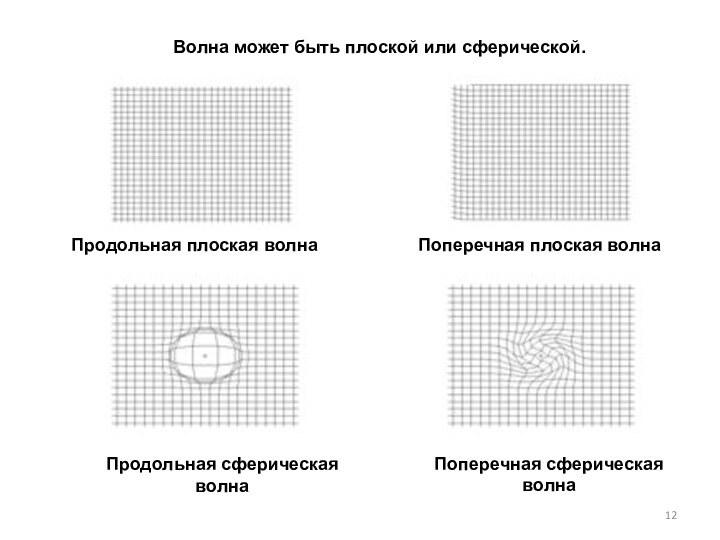
Волна может быть плоской или сферической.
Продольная плоская волна
Поперечная
плоская волна
Продольная сферическая волна
Поперечная сферическая волна
Слайд 13 Бегущими волнами называются волны, которые переносят в пространстве
энергию.
Перенос энергии волнами характеризуется вектором
плотности потока энергии (вектор Умова). 5.11. Уравнение бегущей волны. Фазовая скорость. Волновое уравнение.
Русский физик, философ, Николай Алексеевич Умов (1846—1915)
Направление вектора Умова совпадает с направлением переноса энергии.
Модуль вектора равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны.
Слайд 14 Рассмотрим плоскую волну, предполагая, что
колебания носят гармонический характер, а ось х совпадает с
направлением распространения волныВолновые поверхности перпендикулярны оси х.
Все точки волновой поверхности колеблются одинаково.
Смещение будет зависеть только от x и t :
Расстояние x волна пройдет за время:
Тогда уравнение бегущей волны без учета начальной фазы будет иметь вид:
Слайд 15
Для характеристики волн используется волновое число:
Фазовой скоростью называется
скорость перемещения волны:
Полное уравнение бегущей волны с учетом начальной
фазы:С учетом k уравнение бегущей волны будет иметь вид:
Слайд 16
Уравнение сферической бегущей волны:
r — расстояние от
центра волны до рассматриваемой точки среды
Фазовая скорость волны зависит
от частоты волны: Это явление называют дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется диспергирующей средой.
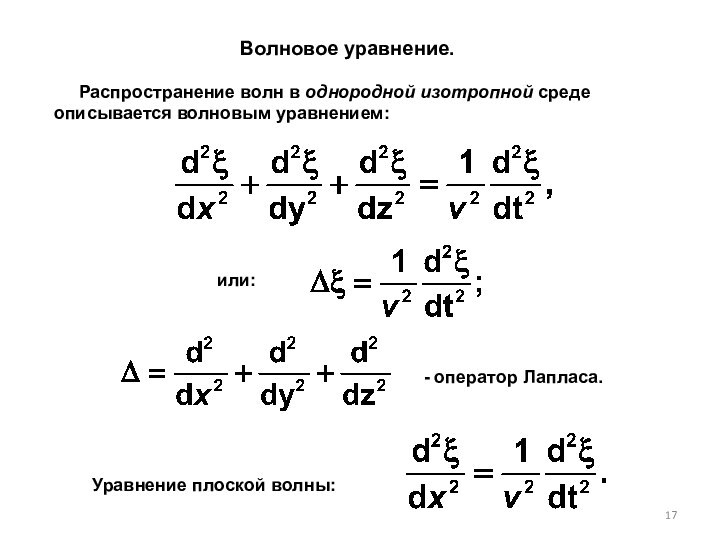
Слайд 17 Распространение волн в однородной изотропной
среде описывается волновым уравнением:
- оператор Лапласа.
Уравнение плоской волны:
Волновое
уравнение. или:
Слайд 18
5.12. Интерференция волн.
Когерентными называются волны, если разность их
фаз остается постоянной во времени.
Когерентными
могут быть лишь волны, имеющие одинаковую частоту. Наложение когерентных волн вызывает усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих воли.
Это явление называется интерференцией волн.
Слайд 19 d1 и d2 — расстояния от источников волн
до рассматриваемой точки C, k — волновое число, 1
и 2 — начальные фазы обеих накладывающихся сферических волн. Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками S1 и S2 .
Слайд 20
Условие максимума:
разность хода волн равна целому числу длин
волн.
При наложении когерентных волн в какой-либо
точке пространства амплитуда колебаний этой точки будет зависеть от разности расстояний от источников до рассматриваемой точки. Разность расстояний называется разностью хода.
В этом случае волны в рассматриваемой точке приходят с одинаковыми фазами и усиливают друг друга – амплитуда колебаний этой точки максимальна и равна удвоенной амплитуде.
Слайд 21
разность хода волн равна нечетному числу длин полуволн.
Волны приходят в рассматриваемую точку в противофазе
и гасят друг друга. Амплитуда колебаний данной точки равна нулю.Условие минимума:
Слайд 22
Стоячие волны
Другой частный случай интерференции
- стоячие волны.
Стоячие волны образуются
при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами. Две плоские волны распространяются навстречу друг другу вдоль оси х в среде без затухания (одинаковые амплитуды и частоты).
Уравнение стоячей волны.
Слайд 23 Сложим уравнения прямой и обратной
волн и получим уравнение стоячей волны:
Точки, в которых амплитуда колебаний максимальна, называются пучностями стоячей волны, а точки, в которых амплитуда колебаний равна нулю, называются узлами стоячей волны.Слайд 24 Амплитуда стоячей волны изменяется и
определяется выражением:
В точке, где:
амплитуда колебаний достигает максимального
значения, равного 2А.В точке, где:
амплитуда колебаний обращается в нуль.
Слайд 25 Координаты пучностей и узлов можно
получить из записанных уравнений:
Из этих выражений
следует, что расстояния между двумя соседними пучностями и двумя соседними узлами одинаковы и равны:Расстояние между соседними пучностью и узлом стоячей волны равно:
Слайд 26
Эффект Доплера.
Доплер (1803-1853) – австрийский физик, математик
и астроном.
Эффектом Доплера называется изменение частоты колебаний,
воспринимаемой приемником, при движении источника колебаний и приемника относительно друг друга.Случай 1. Источник звука неподвижен, наблюдатель движется.





























