- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Синусоидальный ток
Содержание
- 2. Переменный ток по величине (а), по направлению (б), по величине и направлению (в)
- 3. Параметры синусоидального токаПериод переменного токаЧастота колебанийАмплитуда токаУгловая частотаНачальная фазаФазаСреднее значение токаДействующее значение тока
- 4. Действующие значения тока, напряжения, эдс синусоидального тока
- 5. Представление синусоидального тока вращающимся вектором
- 6. Векторные диаграммы токов (а), тока и напряжения (б)
- 7. Период переменного токаСинусоидальный ток является частным случаем
- 8. Частота колебанийВеличина, обратная периоду, называется частотой колебаний, которая
- 9. Синусоидальный токПовсеместное применение получил периодический ток, являющийся
- 10. ФазаАргумент α t = ωt + ψi,
- 11. Начальные фазы синусоидальных напряжения (а) и тока (б)
- 12. Векторная диаграммаСовокупность векторов, изображающих синусоидальные токи, напряжения
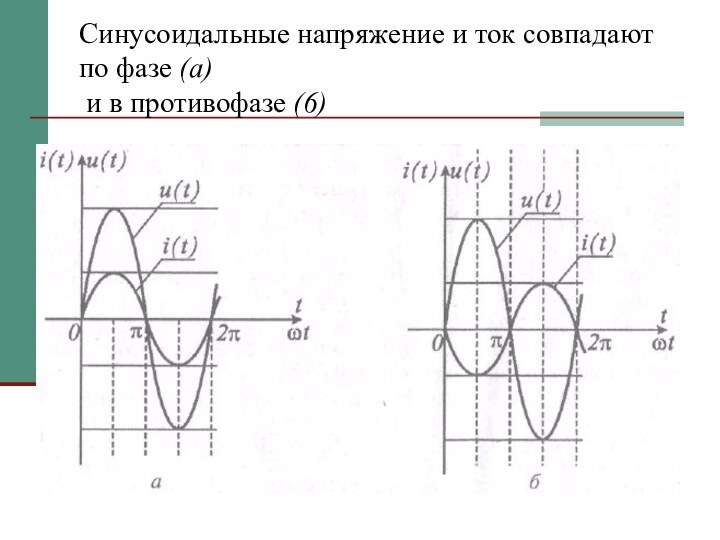
- 13. Синусоидальные напряжение и ток совпадают по фазе (а) и в противофазе (6)
- 14. Среднее значение периодического переменного токаСреднее значение периодического
- 15. Средневыпрямленный токСредневыпрямленным током Icp, как средним значением
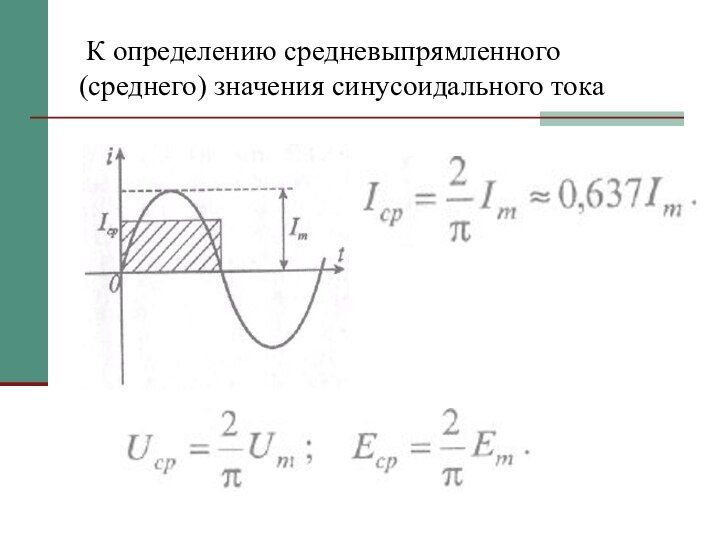
- 16. К определению средневыпрямленного (среднего) значения синусоидального тока
- 17. Действующее значение периодического переменного токаДействующее значение периодического
- 18. Действующий токгде Ri 2dt - есть энергия,
- 19. Представление синусоидального тока комплексными величинамиЛюбое комплексное число,
- 20. Алгебраическая, тригонометрическая и показательная формы
- 21. Представление синусоидального тока вращающимся вектором Если аргумент
- 22. Комплексное число А (а) и оператор вращения (б)
- 23. Мнимая и вещественная частиМнимая часть представляет собой синусоидальный ток.Вещественная часть представляет собой косинусоидальный ток.
- 24. Комплексный мгновенный и действующий синусоидальный ток
- 25. Изображение синусоидального тока комплексными величинамиСинусоидальный ток
- 26. Изображение комплексного тока синусоидальным токомЛюбая из комплексных
- 27. Уравнения для напряжений и эдс
- 28. Закон Ома для участка цепи синусоидального тока
- 29. Закон Ома для участка цепи синусоидального тока
- 30. Комплексное электрическое сопротивление
- 31. Скачать презентацию
- 32. Похожие презентации
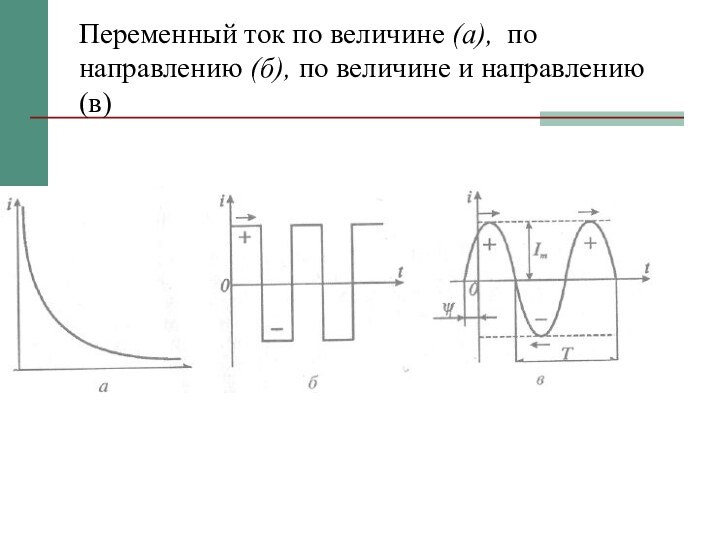
Переменный ток по величине (а), по направлению (б), по величине и направлению (в)




















![Синусоидальный ток Изображение комплексного тока синусоидальным токомЛюбая из комплексных величин I m(t], Iт, I](/img/tmb/11/1045485/32721238b0d39fdc7e18e6f6539528b8-720x.jpg)





Слайд 3
Параметры синусоидального тока
Период переменного тока
Частота колебаний
Амплитуда тока
Угловая частота
Начальная
фаза
Фаза
Среднее значение тока
Действующее значение тока
Слайд 7
Период переменного тока
Синусоидальный ток является частным случаем периодического
переменного тока, значение которого в любой момент времени t
определяется мгновенным током:где k = 1,2,3 ...; Т– период переменного тока, измеряемый в секундах (с).
Периодом Т переменного тока i (t) называется промежуток времени t, через который цикл изменения тока повторяется, a k указывает на номер цикла.
Слайд 8
Частота колебаний
Величина, обратная периоду, называется частотой колебаний,
которая измеряется
в герцах(Гц) и указывает на число колебаний за одну
секунду, т. е. на число периодов переменного тока, укладывающихся за время, равное одной секунде.
Слайд 9
Синусоидальный ток
Повсеместное применение получил периодический ток, являющийся синусоидальной
функцией времени и называемый синусоидальным током
где Im - амплитуда
тока, ω = 2π/Т = 2πf— угловая частота,
ψ — начальная фаза.
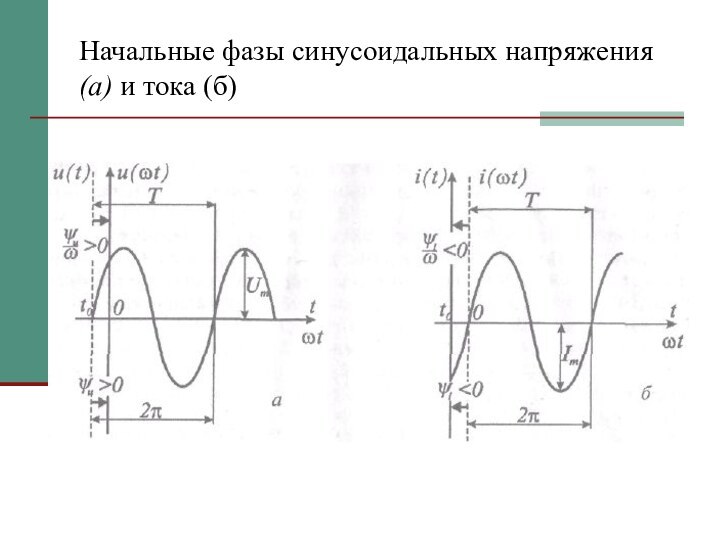
Слайд 10
Фаза
Аргумент α t = ωt + ψi, измеряемый
в градусах или в радианах, определяет фазный угол синусоидальной
функции тока в любой момент времени и называется фазой.Если t =0, то α0 = ψi, есть начальная фаза тока, т. е. значение фазы синусоидального тока в начальный момент времени.
Если α0 = 0, то ψi = – ωt0 т. е. в точке t0 начальная фаза тока ψi < 0;
Слайд 12
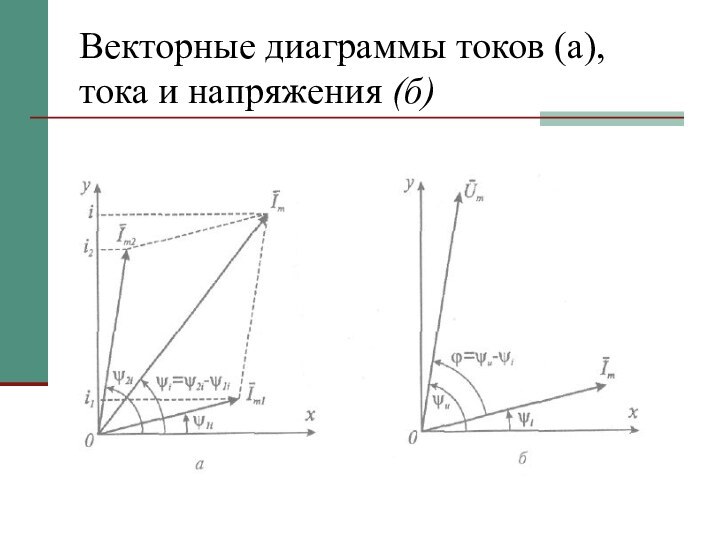
Векторная диаграмма
Совокупность векторов, изображающих синусоидальные токи, напряжения и
ЭДС одинаковой частоты в начальный (или в любой один
и тот же) момент времени, называется векторной диаграммой.
Слайд 14
Среднее значение периодического переменного тока
Среднее значение периодического переменного
тока Iср за период T обычно определяют из геометрических
представлений: площадь прямоугольника с основанием Т/2 и высотой Iср приравнивают площади, ограниченной кривой тока i(t), т. е.
Слайд 15
Средневыпрямленный ток
Средневыпрямленным током Icp, как средним значением тока
за время положительной полуволны, т. е. за половину периода:
Слайд 17
Действующее значение периодического переменного тока
Действующее значение периодического переменного
тока (действующий ток) I определяют из энергетических представлений: действующий
ток равен по величине такому постоянному току I, который в активном сопротивлении R за период Т выделяет такое количество энергии, как данный переменный ток i, т. е.
Слайд 18
Действующий ток
где Ri 2dt - есть энергия, выделяемая
периодическим переменным током i в активном сопротивлении R за
время dt.Здесь под интеграл ток i входит в квадрате: отрицательная половина синусоидального тока дает такой же вклад в количество выделяемой энергии, как и положительная, поэтому интеграл берется за период Т.
Слайд 19
Представление синусоидального тока комплексными величинами
Любое комплексное число, обозначаемое
À или А, можно изобразить на комплексной плоскости
точкой с радиусом - вектором À и представить в алгебраической, тригонометрической и показательной формах.
Слайд 20
Алгебраическая, тригонометрическая и показательная формы комплексного числа
где -
модуль комплексного числа;
а – вещественная часть комплексного числа;
b — мнимая часть комплексного числа;
α = arctg b/a — аргумент комплексного числа.
Слайд 21
Представление синусоидального тока вращающимся вектором
Если аргумент α является
линейной функцией времени t, т.е. , то и графическое
представление комплексной функции À(t) аналогично представлению синусоидального тока вращающимся вектором
Слайд 23
Мнимая и вещественная части
Мнимая часть представляет собой синусоидальный
ток.
Вещественная часть представляет собой косинусоидальный ток.
Слайд 25
Изображение синусоидального тока комплексными величинами
Синусоидальный ток
i(t)
= Im1sin (ωtk + ψi),
имеющий амплитуду Iт, круговую
частоту ω и начальную фазу ψi, однозначно изображается одной из комплексных величин: комплексным мгновенным синусоидальным током I(t), комплексной амплитудой тока I или комплексным током I.
Слайд 26
Изображение комплексного тока синусоидальным током
Любая из комплексных величин
I m(t], Iт, I может быть представлена синусоидальным током
i(t). Слайд 28 Закон Ома для участка цепи синусоидального тока без
источников ЭДС
Комплексная амплитуда тока в цепи синусоидального тока равна
отношению комплексной амплитуды напряжения к комплексному электрическому сопротивлению цепи.





























