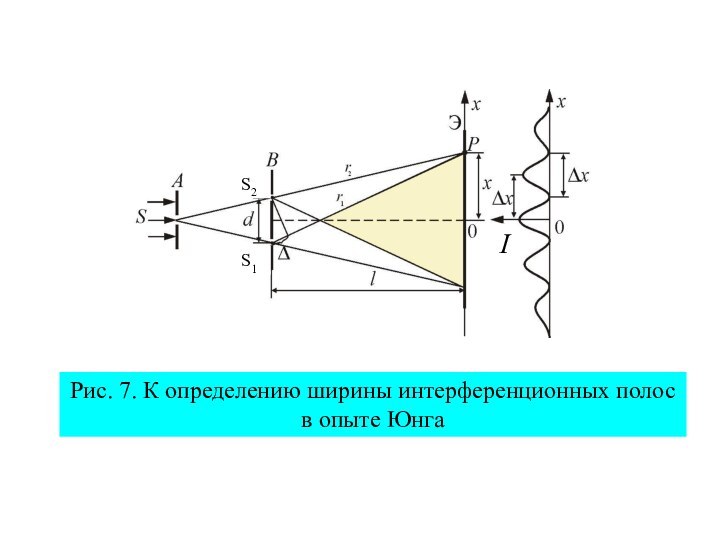
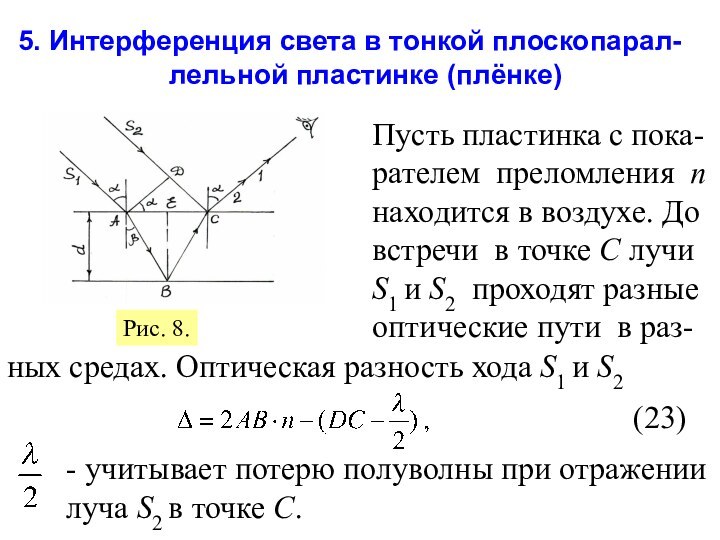
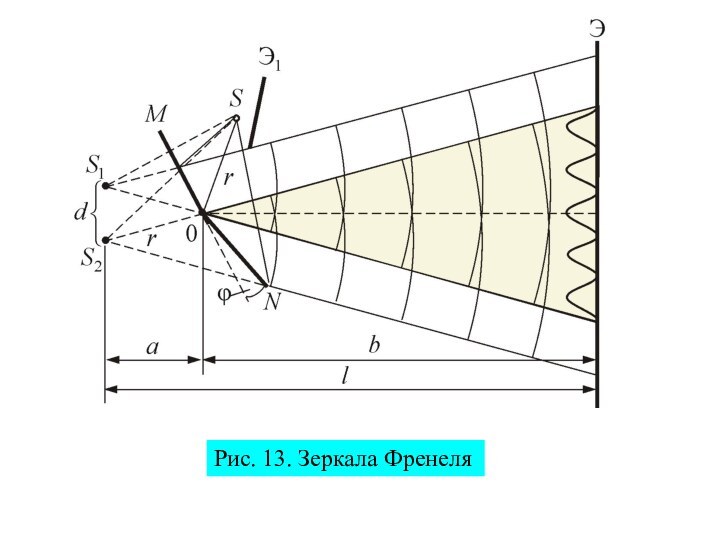
оптика –это раздел оптики, в котором изучается круг явлений
с точки зрения волновой природы све-та.Максвелл (1831 – 1879), обобщая законы электромагнетизма, пришел к выводу об электромагнитной природе света.
В электромагнитной волне колеблются векторы и . Фзиологические, фотохими-ческие, фотоэлектрические и другие действия света вызываются колебаниями электрического вектора . В дальнейшем мы будем называть его