- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теория струн и квантовая хромодинамика
Содержание
- 2. Что мы знаем о КХДТеория сильных взаимодействий,
- 4. При низких энергиях - непертурбативная физика; конфайнмент
- 5. Фазовая диаграмма в КХД (μ, Т)При высоких
- 6. Что мы не знаем про КХД?Как устроено
- 7. Гипотеза дуальности (Maldacena 97, Поляков 77-97)Струна в
- 8. Интерпретация дополнительных измерений5-я координата в AdS5 отвечает
- 9. Дуальность-явная реализация сценария «мира на бране»(Рубаков-Шапошников,83)N солитонных
- 10. Соответствие между параметрами струныи параметрами калибровочной теорииТаким
- 11. Каково соответствие между состояниями струны и объектами
- 12. Дуальность и результаты в теории поляПертурбативный режим
- 13. 3. Струнное описание теории возмущений позволяет
- 14. Первые 4 члена разложения совпадают с недавними явнымивычислениями фейнмановских диаграмм!(Beisert-Eden-Staudacher 06,Bern-Kosover-Dixon-Smirnov 06 4-loops,Lipatov et.al 04 3-loops)
- 15. Непертурбативная КХД1. Информация о IR масштабе неабелевойкалибровочной
- 16. Теория на мировой поверхности флейворных бран сводится
- 17. Для гармоник получаем 4-х мерное
- 18. 2. Вычисление Вильсоновских петельВильсоновская петля- граница мировой
- 19. 2 типа струн в КХД: «электрические» и
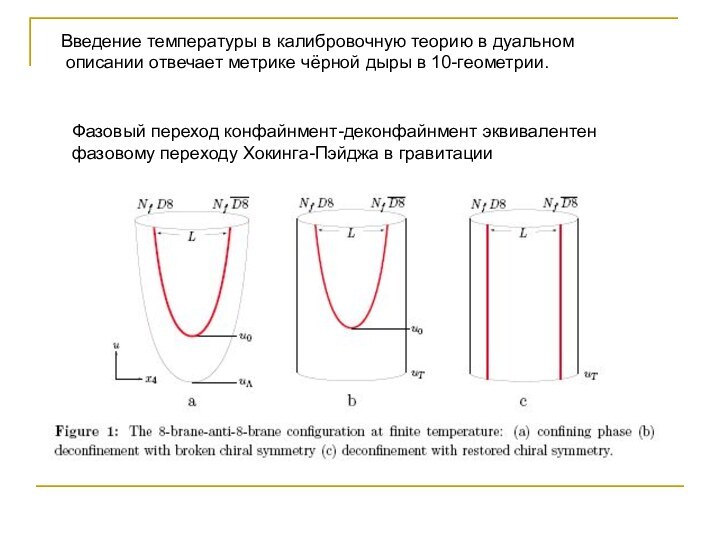
- 20. Введение температуры в калибровочную теорию в дуальном
- 21. Дуальное описание даёт аргументы в пользу того,
- 22. Введение химпотенциала эквивалентно введение U(1)связности на флэйворной
- 23. Скачать презентацию
- 24. Похожие презентации
Что мы знаем о КХДТеория сильных взаимодействий, совместная с доступными экспериментальными даннымиВ области высоких энергий в силу асимптотической свободы режим слабой связи






















Слайд 2
Что мы знаем о КХД
Теория сильных взаимодействий, совместная
с доступными экспериментальными данными
асимптотической свободы режим слабой связиСлайд 4 При низких энергиях - непертурбативная физика; конфайнмент цветных
степеней свободы, спонтанное нарушение киральной симметрии.
Параметры порядка - конденсаты
Эффективное
описание – киральная теория возмущений, в которой эффективные степени свободы - легкие мезоны. Барионы в киральном лагранжиане - солитоны
Слайд 5
Фазовая диаграмма в КХД (μ, Т)
При высоких температурах
фазовый переход конфайнмент-деконфайнмент и восстановление киральной симметрии. При высоких
плотностях новые нетривиальные фазы; color-flavor locking phase, color superconductivityКХД на решетках – указание на существенный вклад протяженных объектов в вакуумные характеристики
Слайд 6
Что мы не знаем про КХД?
Как устроено основное
состояние, вакуум ?
Много моделей, но нет количественного описания
Какое соотношение между температурами различных фазовых переходов?
Какова роль высоких порядков теории возмущений ?
Какова природа КХД струны?
2 типа струн, «магнитные» и «электрические»?
Слайд 7
Гипотеза дуальности (Maldacena 97, Поляков 77-97)
Струна в нетривиальном
10-мерном
пространстве дуальна калибровочной
теории поля с максимально возможной
суперсимметрией в 4-х
измеренияхМетрика 10-ти мерного пространства
AdS5 имеет вид
Слайд 8
Интерпретация дополнительных измерений
5-я координата в AdS5 отвечает масштабу
в
4-х мерной теории поля на границе в
голографическом описании. Остальные
координаты
в S5 соответствуют вакуумнымзначениям скалярных полей
суперсимметричной теории
В теории с меньшей суперсимметрией
вместо S5 более сложная геометрия,
задающая параметры теории
Слайд 9
Дуальность-явная реализация сценария
«мира на бране»(Рубаков-Шапошников,83)
N солитонных объектов
в теории струн – D3 бран
индуцируют в многомерном
пространстве метрикуи внешнее поле. 4-х мерное пространство, «наш мир»,
определен на солитоне в многомерном пространстве.
Струна - «пробник» 4-х мерной физики на бране.
D3
AdS5
Слайд 10
Соответствие между параметрами струны
и параметрами калибровочной теории
Таким образом,
в режиме сильной связи
натяжение струны велико и она
может быть описана квазиклассически. С другой
стороны режим слабой связи в теории поля
соответствует квантовой струне.
Слайд 11 Каково соответствие между состояниями струны и объектами в
калибровочной теории?
Состояние струны = оператор в калибровочной теории
Энергия струны
= аномальная размерностьоператора, которая определяет зависимость
физических величин от энергии процесса
Слайд 12
Дуальность и результаты в теории поля
Пертурбативный режим в
КХД
Струнное(твисторное) описание позволило сформулировать новую эффективную диаграммную технику в
теории Янга-Миллса (MHV формализм). (Cachazo,Witten,Swrchk 04,Rosly, A.G. 06).С её помошью вычислены новые петлевые вклады в амплитуды с участием глюонов. Обнаружена скрытая интегрируемость уравнений эволюции в КХД. Она отвечает интегрируемости струны в 10-ти мерии в дуальном описании. Основные результаты для SUSY ЯМ, но есть результаты и в КХД. Новые симметрии в теории возмущений в КХД!
(Lipatov 93,Faddeev Korchemsky 94, Braun Derkachev Manashov 98, Minahan-Zarembo 02)
Слайд 13
3. Струнное описание теории возмущений позволяет
провести
суммирование ряда теории возмущений
для некоторых величин!
Пример: аномальная размерность оператора
твиста 2с большим спином (в N=4 теории). В обычной КХД она
определяет зависимость момента структурной
функции от энергии.
Предсказание для аномальной размерности,
следующее из струнного описания
Слайд 14
Первые 4 члена разложения совпадают с недавними явными
вычислениями
фейнмановских диаграмм!(Beisert-Eden-Staudacher 06,
Bern-Kosover-Dixon-Smirnov 06 4-loops,Lipatov et.al 04 3-loops)
Слайд 15
Непертурбативная КХД
1. Информация о IR масштабе неабелевой
калибровочной теории
зашифрована в
геометрии 10-мерного пространства с
горизонтом (Witten 98).
2. Впервые получен
киральный лагранжианв теории Янга-Миллса с кварками «из
первых принципов»! Предполагается, что
Nc >> Nf, то есть Nc задают фоновую
геометрию в которой распостраняются Nf
флэйворных бран. Киральный лагранжиан
возникает как теория на мировой поверхности
флэйворных бран с калибровочной группой
Слайд 16
Теория на мировой поверхности
флейворных бран сводится к
5-ти мерной калибровочной теории(Sakai-Sugimoto 05)
Z – радиальная «ренормгрупповая» координата,
по которой вводится разложение по модам
Слайд 17
Для гармоник получаем 4-х мерное
действие
где
киральное мезонное поле U возникает из
z-компоненты
калибровочного поля
, а константы имеют видБарион автоматически оказывается солитонным объектом
D4 – браной, намотанной на цикл, а барионный заряд
совпадает с топологическим зарядом на флэйворной бране
Слайд 18
2. Вычисление Вильсоновских петель
Вильсоновская петля- граница мировой поверхности
струны, протяженной в радиальном направлении. Задача
Эффективно сводится к вычислению
площади мировой поверхности струны во внешней метрике(Maldacena,Lee Rey 98)
Слайд 19
2 типа струн в КХД: «электрические» и «магнитные»
В
теории струн есть «подходящие» объекты – фундаментальная (электрическая) струна
(T~g)D1 (магнитная) струна (T~1/g) которая имеет
большое натяжение в режиме слабой связи. Она
является «родственником» абрикосовской струны
В последнее время были обнаружены новые
неабелевы струны в калибровочных теориях со
скалярами.(Hanany,Tong,Shifman-Yung,A.G 04-07)
Струны Абрикосова и Zn струны -абелевы и могут
рассматриваться как связанное состояние неабелевых
струн. Найден новый объект-монополь в фазе Хиггса,
локализованный на поверхности неабелевой струны.
Очень близко к результатам в КХД на решетке!
Слайд 20
Введение температуры в калибровочную теорию в дуальном
описании
отвечает метрике чёрной дыры в 10-геометрии.
Фазовый переход конфайнмент-деконфайнмент эквивалентен
фазовому
переходу Хокинга-Пэйджа в гравитации
Слайд 21
Дуальное описание даёт аргументы в пользу того, что
фазовые
переходы К-Д и переход с восстановлением киральной симметрии разнесены
по энергииНеожиданное предсказание для отношения вязкости к
энтропии в калибровочной теории в гидродинамическом
режиме
S-плотность энтропии, экспериментально наблюдаемое
отношение. Гипотеза - это нижняя граница в общей ситуации
Kovtun,Son,Starinets 04
Слайд 22
Введение химпотенциала
эквивалентно введение U(1)
связности на флэйворной бране
Предсказание
-в КХД с
химпотенциалом возникает
смешивание векторных и аксиальных
мезонов из члена
CSHarvey 07





























