- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Уравнение Ван-дер-Ваальса.
Содержание
- 2. Поведение реальных газов в той или иной
- 3. Модель Ван-дер-Ваальса. Приступая к получению приближенного
- 4. Термическим уравнением состояния (или, часто, просто уравнением
- 5. Вывод уравнения Наиболее известны два способа получения
- 6. Видно, что это уравнение фактически является уравнением
- 7. Далее предположим, что частицы данного газа являются
- 8. Стоит заметить, что вычитаемый объём b не
- 9. Число частиц, которые находятся непосредственно у стенок,
- 10. Окончательное уравнение:
- 11. Скачать презентацию
- 12. Похожие презентации
Поведение реальных газов в той или иной степени отличается от поведения идеального газа, описываемого уравнением Менделеева-Клапейрона. Отклонения зависят не только от того, с каким газом — кислородом, азотом и т. д. - мы имеем дело, но





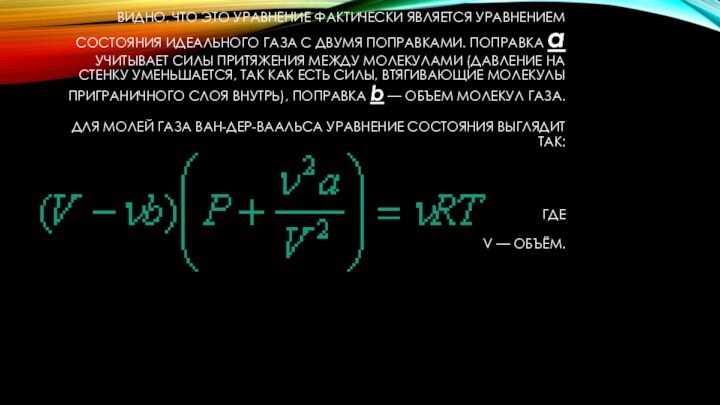





Слайд 3 Модель Ван-дер-Ваальса. Приступая к получению приближенного уравнения состояния
реального газа, будем считать, что взаимодействие молекул приводит лишь
к небольшим поправкам в уравнении состояния идеального газа. При достаточно высоких температурах и малых плотностях газа искомое уравнение должно приводить к тем же результатам, что и уравнение Менделеева—Клапейрона. Свойства большинства газов близки к свойствам идеального газа, когда они находятся при температурах, достаточно далеких от точки конденсации, т. е. когда между молекулами отсутствует взаимодействие и когда собственный объем молекул газа мал по сравнению с объемом газа. Вблизи точки конденсации (при высоком давлении и низкой температуре) свойство газов значительно отличается от свойств идеального газа. В этих случаях говорят о реальных газах.Слайд 4 Термическим уравнением состояния (или, часто, просто уравнением состояния)
называется связь между давлением, объёмом и температурой. Для одного моля
газа Ван-дер-Ваальса оно имеет вид:где
p — давление,
V — молярный объём,
T — абсолютная температура,
R — универсальная газовая постоянная.
Слайд 5 Вывод уравнения Наиболее известны два способа получения уравнения: традиционный
вывод самого Ван-дер-Ваальса и вывод методами статистической физики.
Традиционный вывод
Рассмотрим
сначала газ, в котором частицы не взаимодействуют друг с другом, такой газ удовлетворяет уравнению состояния идеального газа:Слайд 6 Видно, что это уравнение фактически является уравнением состояния
идеального газа с двумя поправками. Поправка a УЧИТЫВАЕТ силы
притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка b — объем молекул газа. Для молей газа Ван-дер-Ваальса уравнение состояния выглядит так: где V — объём.Слайд 7 Далее предположим, что частицы данного газа являются упругими
сферами одинакового радиуса r. Так как газ находится в
сосуде конечного объёма, то пространство, где могут перемещаться частицы, будет несколько меньше. В исходной формуле следует вычесть из всего объёма некую его часть b, которая, вообще говоря, зависит только от вещества, из которого состоит газ. Таким образом, получается следующее уравнение:Слайд 8 Стоит заметить, что вычитаемый объём b не будет
в точности равен суммарному объёму всех частиц. Если частицы
считать твёрдыми и абсолютно упругими шариками, то вычитаемый объём будет примерно в четыре раза больше. Это легко объясняется тем, что центры упругих шаров не могут приближаться на расстояние ближе 2r. Далее Ван-дер-Ваальс рассматривает силы притяжения между частицами газа и делает следующие допущения: Частицы распределены равномерно по всему объёму. Силы притяжения стенок сосуда не учитываются, что в общем случае неверно. Частицы, находящиеся внутри сосуда и непосредственно у стенок, ощущают притяжение по-разному: внутри сосуда действующие силы притяжения других частиц компенсируют друг друга.Таким образом, для частиц внутри сосуда силы притяжения не учитываются. А частицы, находящиеся непосредственно у края сосуда, затягиваются внутрь силой, пропорциональной концентрации: