Презентация на тему Векторы

которые при переходе от одной системы координат к
другой

в которых коэффициенты имеют значения

дает длину вектора. Это уже величина ска-
лярная, причем всегда

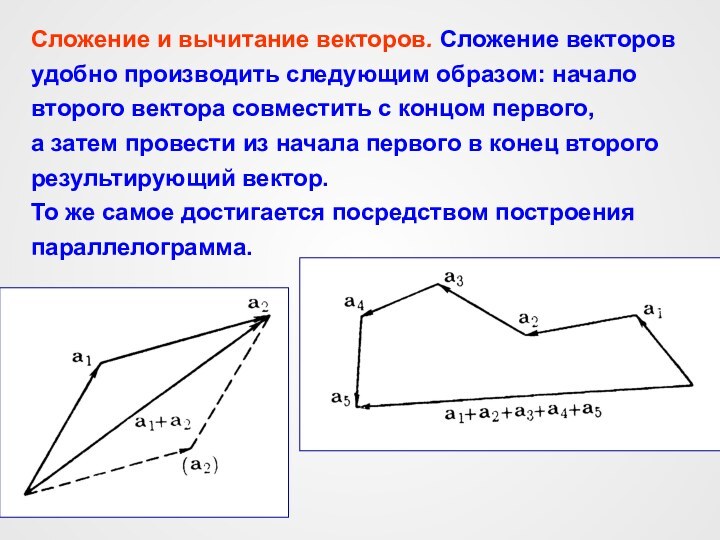
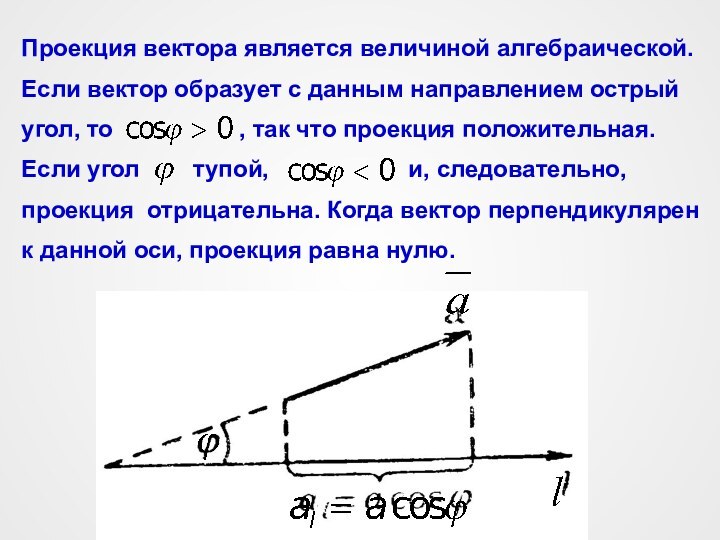
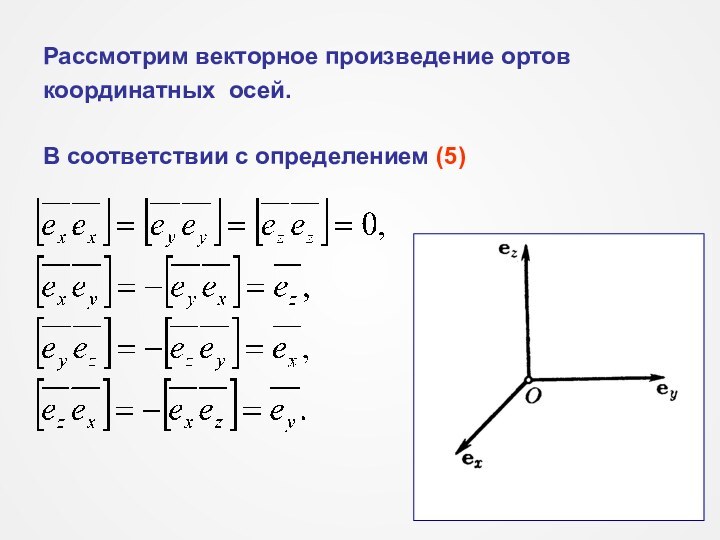
На чертежах векторы изображаются в виде прямолиней-
ных отрезков со стрелкой на конце. Длина отрезка опре-
деляет в установленном масштабе модуль вектора, а
стрелка указывает направление вектора.
Векторы принято обозначать буквами жирного шрифта
(в книгах), либо со стрелочками наверху

Обычная буква используется для обозначения модуля
вектора

Иногда для обозначения модуля используют
символ

векторов:
они коллинеарные, имеют одинаковое направление и
совпадают по

Векторы, направленные вдоль параллельных прямых (в одну и туже или в противоположенные стороны), называются коллинеарными.

Векторы, которые лежат в параллельных плоскостях,
называются компланарными.

Посредством параллельного переноса коллинеарные
векторы могут быть расположены вдоль одной и той же прямой, а компланарные векторы могут быть сведены в одну плоскость.

следующим образом: начало
второго вектора совместить с концом первого,
а

называется
такой вектор , который

на скаляр получается новый вектор
модуль которого

Направление же вектора либо совпадает с направ-лением вектора (если ), либо противополож-но направлению вектора (если ).

Умножение вектора на -1 изменяет направление вектора на обратное.

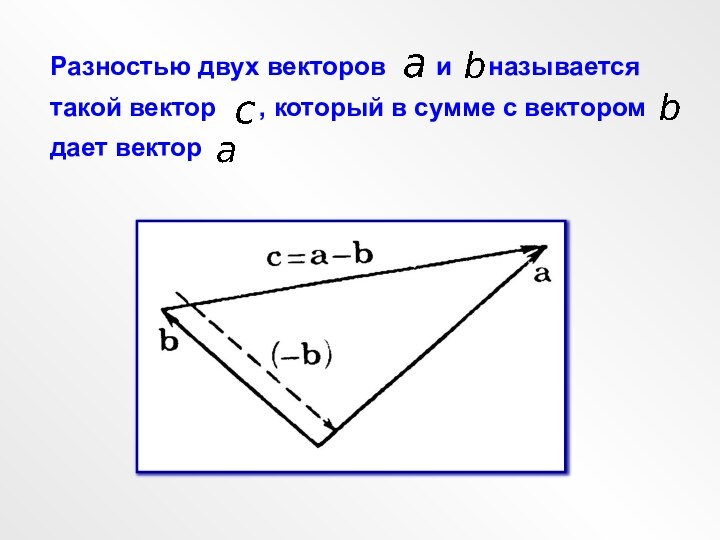
Векторы и имеют одинаковые модули, но
противоположны по направлению

ортом

вектора .
Вычитание из вектора

Всякий вектор можно представить в виде

где - модуль вектора

вектор с модулем, равным единице, имеющим
такое же направление, как и .

является безразмерной
величиной.
Орты можно сопоставлять не только векторам, но
и

- орт координатной оси ,

- орт нормали к кривой или поверхности,

- орт касательной к поверхности и т.д.

некоторые

Линейная зависимость между векторами.
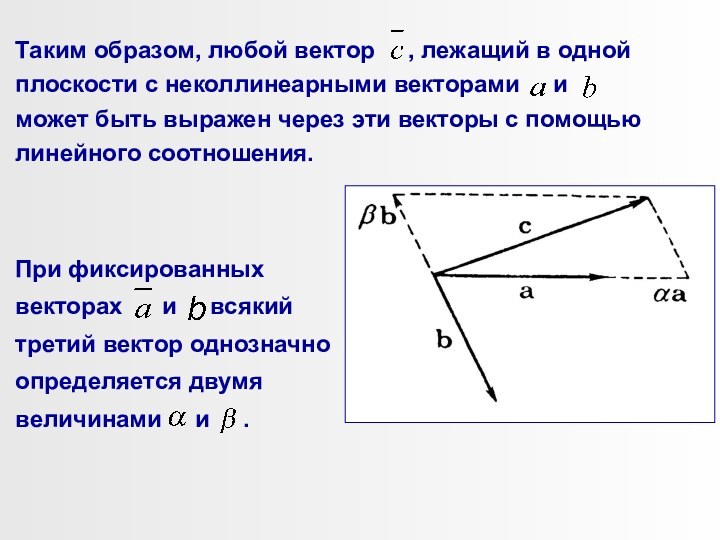
Рассмотрим три неколлинеарных вектора , и ,
которые лежат в одной плоскости.

Любой из них (например, ) можно выразить через два
других с помощью соотношения

можно представить как линейную комбинацию заданных
вектор
Имеем

Каждый из которых некомпланарен с остальными двумя
(то что два вектора всегда компланарны следует из того,
что параллельным переносом всегда можно совместить их
начала и тогда они окажутся расположенными в одной
плоскости).

При фиксированных векторах любой вектор
однозначно определяется тремя величинами ,
каждая из которых может быть как положительной, так и
отрицательной.

зададим осью .
Величина

с данным направлением острый
угол, то

проекциями на ось начала
и конца отрезка, изображающего данный вектор.
В

это расстояние берется со знаком плюс.

В случае

- со знаком минус.

направление равна сумме проекций складываемых
векторов:
Пусть


При суммировании проекций изображенных на

на оси координат.
Из рисунка видно, что вектор

линейной комбинации
ортов

Эта тройка ортов полностью определяет систему
координат и поэтому называется базисом
координатной системы.

равны (с точностью до знака) сторонам
прямоугольного

В общем случае, когда все три
проекции вектора отличны от
нуля

Таким образом, любой вектор можно выразить
через его проекции на координатные оси и орты
этих осей.
В связи с этим проекции на координатные оси
называются компонентами вектора.

Поэтому имеет место соотношение

(1)

(1), получим:
На основании того, что равные векторы имеют равные

(2)

Формулы (2) является аналитическим выражением
правила сложения векторов и справедливы при любом
числе слагаемых.

вектор, проведенный из начала координат
в данную точку.
Его

Следовательно, в соответствии
с (1) радиус-вектор можно
представить в виде

И согласно (2)

можно умножить друг на друга двумя способами:

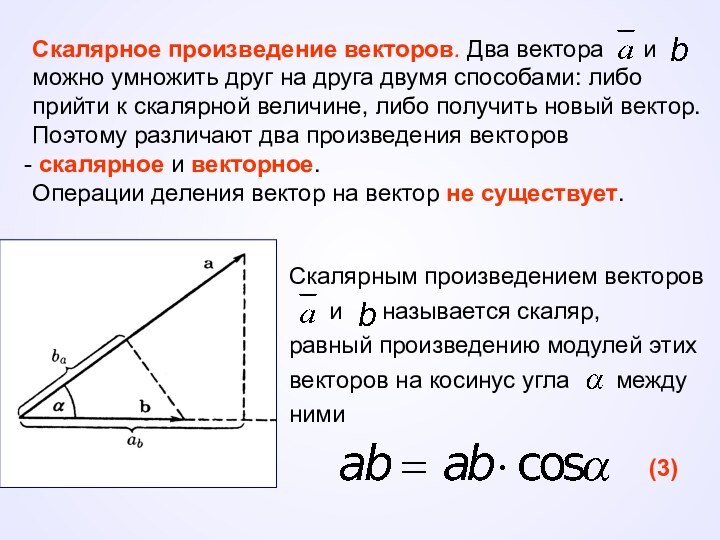
Скалярным произведением векторов
и называется скаляр,
равный произведению модулей этих
векторов на косинус угла между
ними

(3)

остром

Скалярное произведение взаимно перпендикулярных
векторов равно нулю.

Квадрат вектора - скалярное произведение вектора на
самого себя

Квадрат вектора равен квадрату его модуля.
В частности, квадрат любого орта равен единице:

Вследствие взаимной перпендикулярности ортов,
скалярные произведения вида
равны нулю, если

символ, скалярное произведение ортов
координатных осей можно выразить одной

Скалярное произведение коммутативно, т.е. не зависит
от порядка сомножителей

Оно может быть записано несколькими способами

вектора, имеем
Приняв во внимание, что проекция суммы векторов равна

и
при поворотах осей носят такой

Заметим, что при поворотах координатных осей проекции
векторов на эти оси меняются. Однако, величина

от выбора осей не зависит.

Воспользовавшись дистрибутивностью скалярного
произведения и символом Кронекера, получим выраже-
ние скалярного произведения через проекции векторов

(4)

можно
представить в виде
где - орт

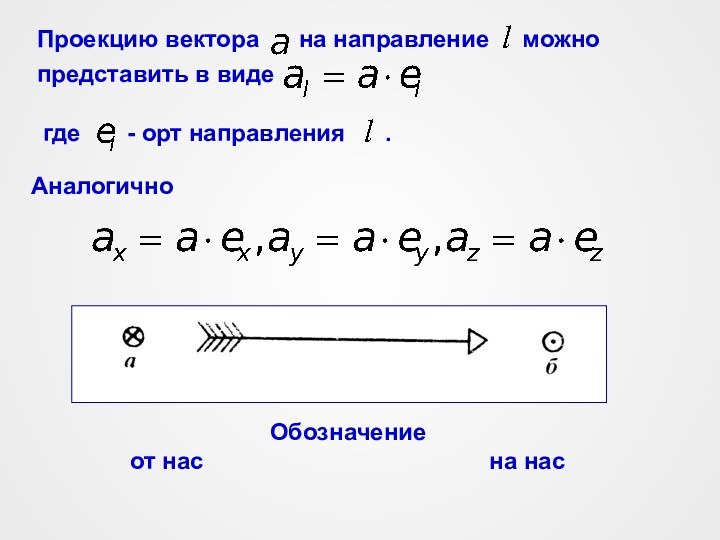
Аналогично

Обозначение
от нас на нас

называется вектор , определяемый
формулой

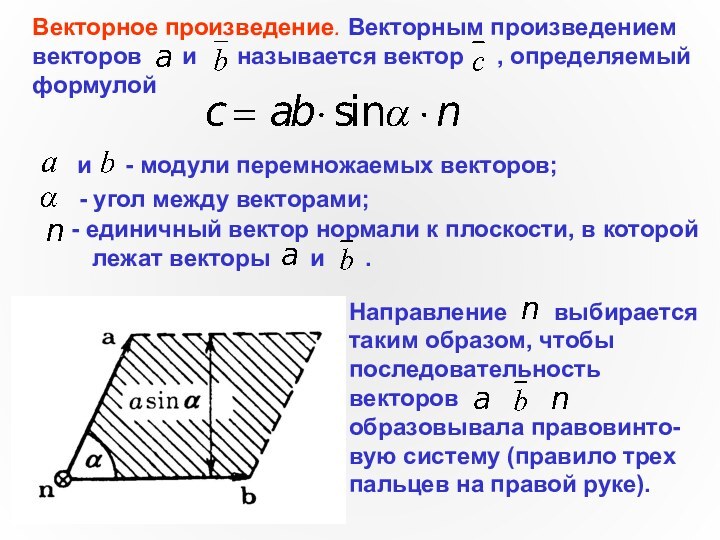
- угол между векторами;

единичный вектор нормали к плоскости, в которой
лежат векторы и .

Направление выбирается таким образом, чтобы
последовательность векторов
образовывала правовинто-вую систему (правило трех пальцев на правой руке).

, то
совершаемый по кратчайшему пути поворот от первого

Символически векторное произведение записывается
или

Таким образом, векторное произведение

Модуль векторного произведения имеет простой
геометрический смысл. Выражение численно
равно площади параллелограмма, построенного на
перемножаемых векторах.

(5)

,
скорость , сила

Направление вектора определено, связав его с направ-
лением вращения от первого сомножителя ко второму.

Векторы типа направление которых связывается с
направлением вращения, называются псевдовекторами
(или аксиальными векторами). При изменении условий,
например при переходе от правой системы координат к
левой (инверсия системы координат), направления
псевдовекторов изменяются на обратные, истинные же
векторы при этом остаются без изменений.

Небольшое отступление

псевдовектором только в том случае, когда оба
перемножаемых вектора

Изменение условия, определяющего направление
псевдовекторов, на обратное приведет в этом случае к изменению знака перед векторным произведением и
одновременно к изменению знака перед одним из
сомножителей. В итоге величина, выражаемая векторным произведением, останется без изменений.

Векторное же произведение истинного вектора на
псевдовектор будет истинным вектором.

первого
сомножителя ко второму, результат векторного
перемножения зависит от порядка

Векторное произведение дистрибутивно, т.е.

же выражение можно представить
в виде определителя:

простой
геометрический смысл – оно
численно равно объему паралле-
лепипеда, построенного на
перемножаемых

Смешанное произведение. Смешанным (или скалярно-
векторным) произведением трех векторов называется
выражение
т.е. скалярное произведение вектора на векторное
произведение векторов и .

Согласно определению

от того, какая из его граней взята в
качестве

Смешанное произведение допускает циклическую
перестановку сомножителей,
т.е. замену каждого из
сомножителей следующим
за ним в цикле.

минус цаб».
Полезной может быть формула квадрата векторного
произведения

временем по известному закону
Проекции этого вектора на координатные оси

(здесь предполагается, что нет пространственного
изменения орт осей!!!).

Тогда вектор получит приращение

со временем можно
охарактеризовать отношением

(6)

соответствующей величины с точкой над ним,
например:
и т.д.
Воспользовавшись таким

Устремляя к нулю, получаем предел, который
называется производной. Поэтому выражение (6)
можно преобразовать к

(7)

взять радиус-вектор
движущейся точки, то

приближенное равенство
переходит в точное.
Тогда дифференциал вектора

И в частности

Заметим, что приращение функции за очень малый, но
конечный промежуток времени приближенно равно

Аналогичную формулу можно записать и для векторной
функции

(8)

(9)

, которая равна произведению скалярной
функции

или

Найдем приращение искомой функции

Представив приращения функций в виде (8) и (9), получим

откуда

это приближенное равенство
превращается в точное.

Первые два слагаемые

Предел третьего слагаемого равен нулю.
Поэтому

и
Приращение этого произведения равно:
Отсюда
(10)
Умножая (10) на

(11)

и (11), имеем
Но из скалярного произведения векторов
имеем
Тогда

или

и
Распишем приращение рассматриваемой функции
Соответственно
Осуществив предельный переход,

вектора .
Очевидно, что вектор

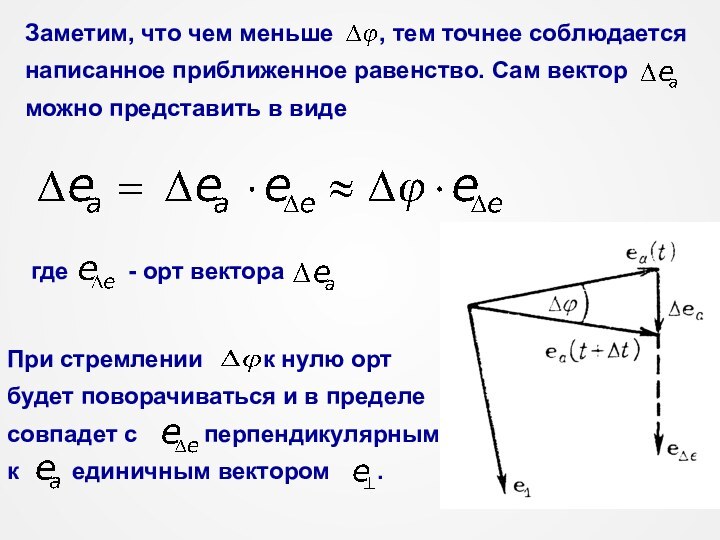
Пусть за очень малый промежуток времени вектор
и вместе с ним орт поворачивается на угол

При малом модуль вектора приближенно
равен углу

(отрезок, изображающий
является основанием
равнобедренного треугольника
со сторонами, равными единице).

тем точнее соблюдается
написанное приближенное равенство. Сам вектор