- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Закон Гука
Содержание
- 2. 2. Обобщенный закон ГукаxzyПри воздействии σx :Аналогично для других напряжений
- 3. 2. Обобщенный закон ГукаИспользуя принцип суперпозиции:εx =
- 4. 2. Объемный закон Гукаxyz111dxdydzРассмотрим изменение объема единичного
- 5. 2. Объемный закон ГукаИспользуем обобщенный закон Гука:εV
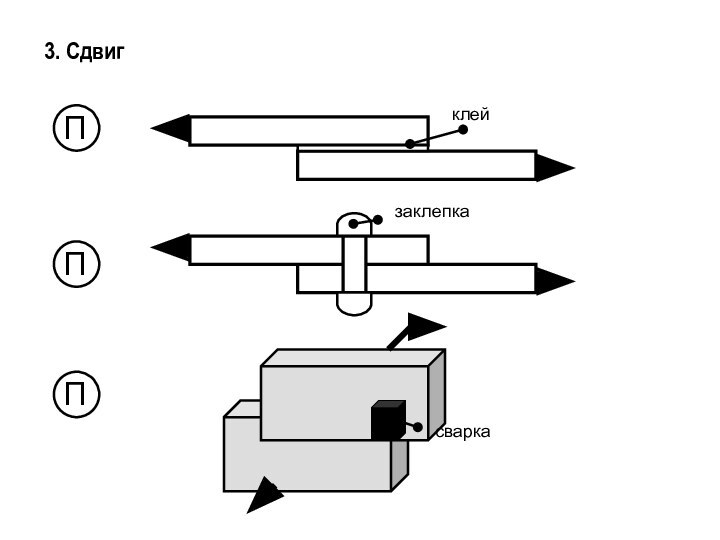
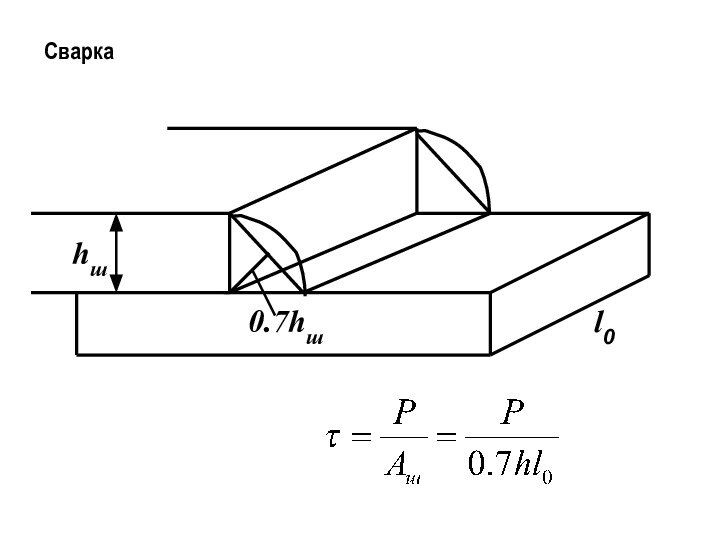
- 6. 3. Сдвигклейсварка
- 7. 3. СдвигРассмотрим состояние т.н. чистого сдвига –
- 8. 3. СдвигРанее было получено:илиσ1 > σ2 >
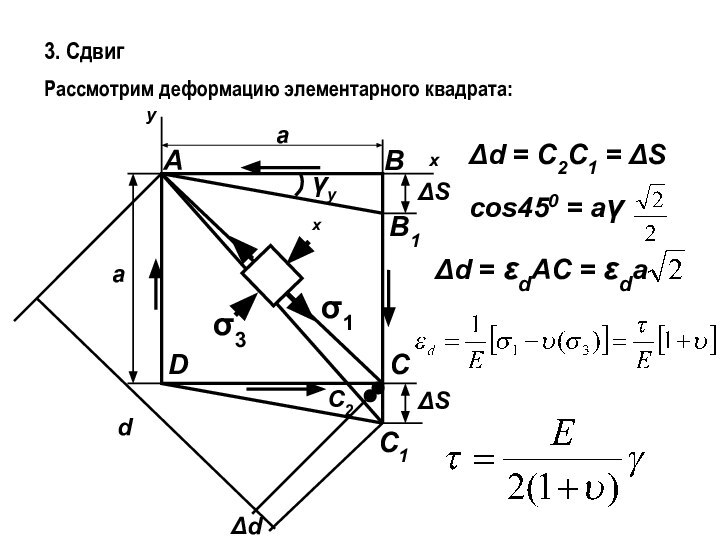
- 9. 3. СдвигРассмотрим деформацию элементарного квадрата:xyааАВСDВ1С1ΔSΔSС2dΔdσ1σ3Δd = C2C1 = ΔScos450 = aγ Δd = εdAC = εda
- 10. 3. СдвигРассмотрим аналогию:- модуль сдвига или «модуль упругости второго рода»
- 11. 3. СдвигПолная сводка уравнений для пространственного напряженного состояния:
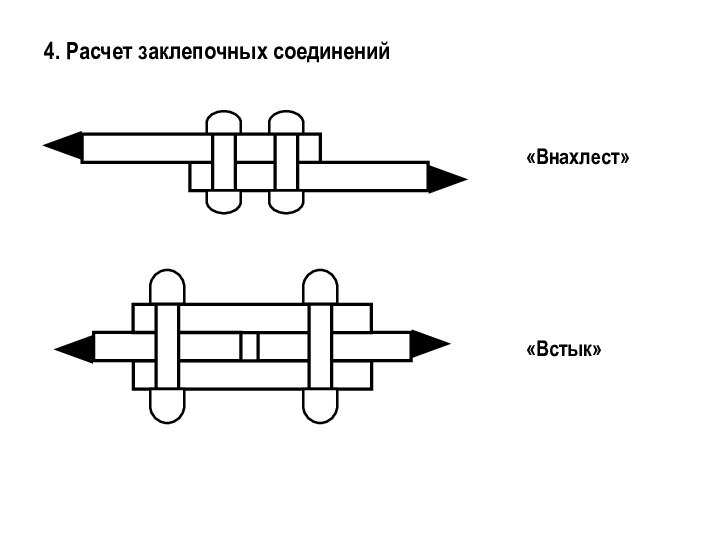
- 12. 4. Расчет заклепочных соединений«Внахлест»«Встык»
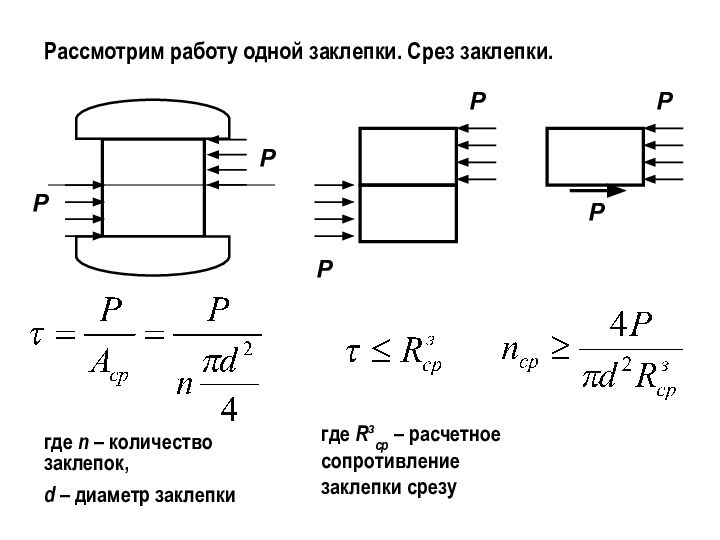
- 13. Рассмотрим работу одной заклепки. Срез заклепки.РРРгде n
- 14. Смятие заклепкиУсловная поверхность смятияdtРеально n = nmax{nср, nсм}
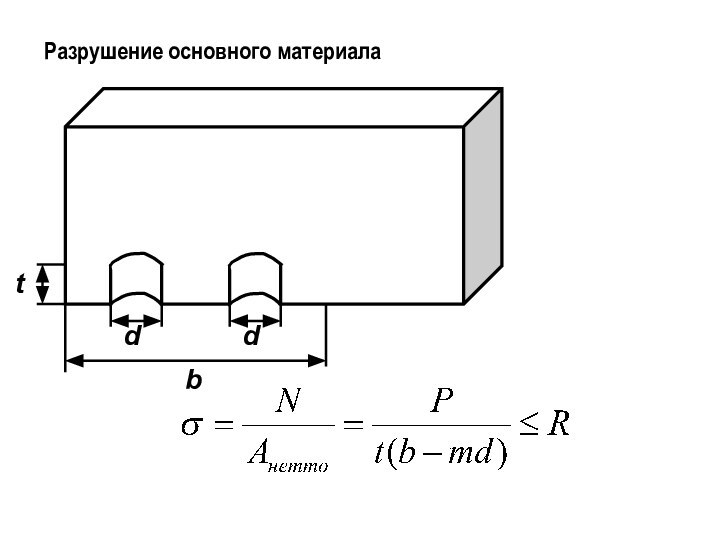
- 15. Разрушение основного материалаddbt
- 16. Скачать презентацию
- 17. Похожие презентации
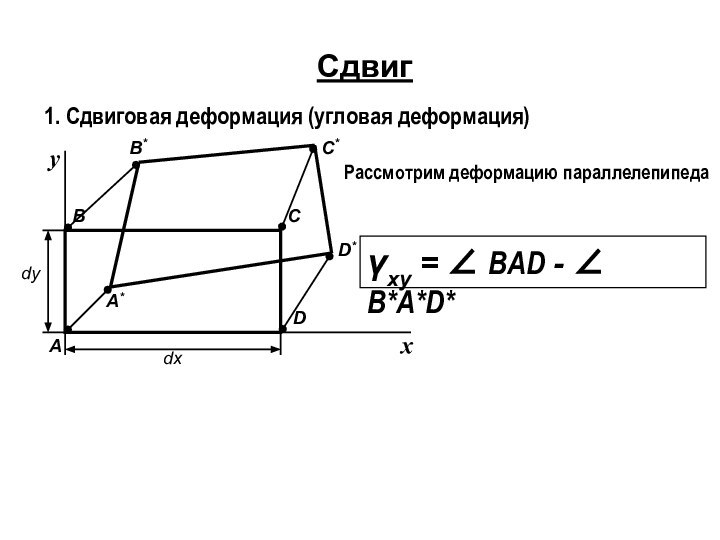






Слайд 3
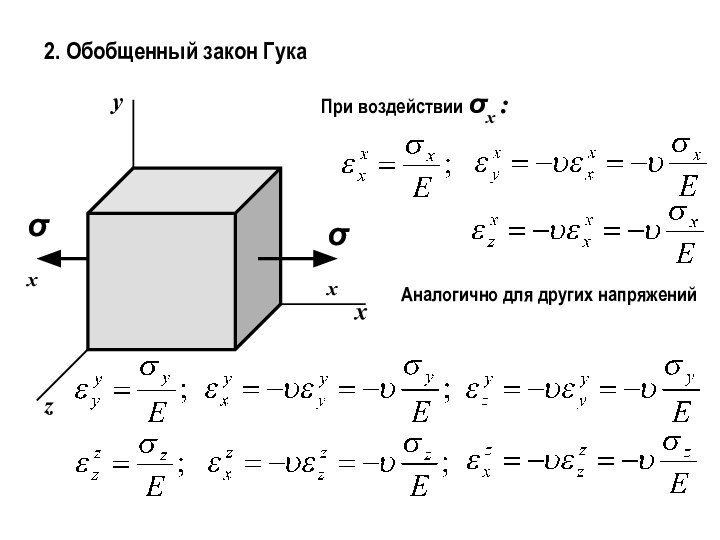
2. Обобщенный закон Гука
Используя принцип суперпозиции:
εx = εxx
+ εxy + εxz =
Обобщенный закон Гука для
изотропного тела
Слайд 4
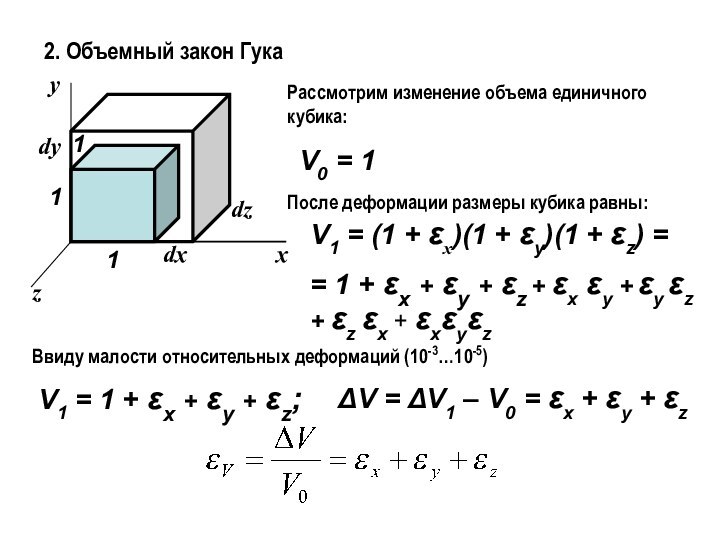
2. Объемный закон Гука
x
y
z
1
1
1
dx
dy
dz
Рассмотрим изменение объема единичного кубика:
V0
= 1
После деформации размеры кубика равны:
V1 = (1 +
εx)(1 + εy)(1 + εz) = = 1 + εx + εy + εz + εx εy + εy εz + εz εx + εxεyεz
Ввиду малости относительных деформаций (10-3…10-5)
V1 = 1 + εx + εy + εz;
ΔV = ΔV1 – V0 = εx + εy + εz
Слайд 5
2. Объемный закон Гука
Используем обобщенный закон Гука:
εV =
1/E[σx + σy + σz -ν(σy + σz +
σx + σz + σx + σy )] = (1 – 2ν)/E (σx + σy + σz)εV = (1 – 2ν)/E (σx + σy + σz)
Объемный закон Гука
σ0 = 1/3 (σx + σy + σz)
Обозначим:
- среднее напряжение
Тогда:
Обозначим:
- объемный модуль упругости
Видно, что νпред = 0.5
Слайд 7
3. Сдвиг
Рассмотрим состояние т.н. чистого сдвига – прямоугольный
элемент не испытывает удлинения сторон, на ┴ площадках действуют
только τα
σα
σα+900
Ранее было получено:
σα = σxcos2α + σysin2α - τyxsin2α
τy1x1 = ½(σx - σy) sin2α + τyxcos2α
В нашем случае на исходных площадках:
σx = σy = 0, τyx = -τ
σα = τ sin2α
τy1x1 = -τ cos2α
σα = 0 при α = 0, ± nπ/2
Всегда σα = - σα+90
Закон «парности» нормальных напряжений при чистом сдвиге
(1)
Слайд 8
3. Сдвиг
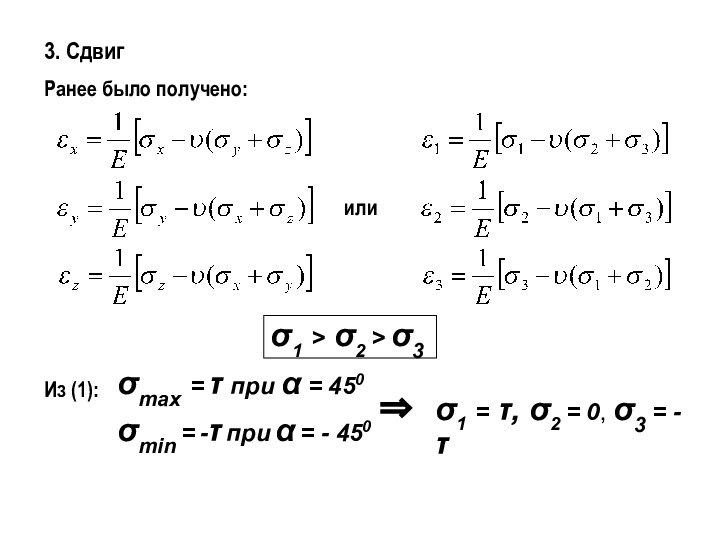
Ранее было получено:
или
σ1 > σ2 > σ3
Из
(1):
σmax = τ при α = 450
σmin = -τ
при α = - 450⇒
σ1 = τ, σ2 = 0, σ3 = -τ





























